卷积

卷积

卷积（Convolution），也叫摺积，是分析数学中一种重要的运算。在信号处理或图像处理中，经常使用一维或二维卷积。

一维卷积

一维卷积经常用在信号处理中，用于计算信号的延迟累积。
假设一个信号发生器每个时刻 \(t\) 产生一个信号 \(\mathcal{x}_{t}\) ，其信息的衰减率为 \(w_{k}\)，即在 \(k − 1\) 个时间步长后，信息为原来的 \(w_{k}\) 倍。假设 \(w_{1}=1\), \(w_{2}=1/2\), \(w_{3}=1/4\)，那么在时刻 \(t\) 收到的信号 \(y_{t}\) 为当前时刻产生的信息和以前时刻延迟信息的叠加：

\[\begin{aligned} y_{t} &=1 \times x_{t}+1 / 2 \times x_{t-1}+1 / 4 \times x_{t-2} \\ &=w_{1} \times x_{t}+w_{2} \times x_{t-1}+w_{3} \times x_{t-2} \\ &=\sum_{k=1}^{3} w_{k} \cdot x_{t-k+1} \end{aligned} \]

我们把 \(w_{1}, w_{2}, \cdots\) 称为滤波器（Filter）或卷积核（Convolution Kernel）。
假设滤波器长度为 m，它和一个信号序列 \(x_{1}, x_{2}, \cdots\) 的卷积为：

\[y_{t}=\sum_{k=1}^{m} w_{k} \cdot x_{t-k+1} \]

信号序列 \(x\) 和滤波器 \(w\) 的卷积定义为：

\[\mathbf{y}=\mathbf{w} \otimes \mathbf{x} \]

其中 \(y \in \mathbb{R}^{m-k+1}\) 为输出矩阵。

一维卷积示例

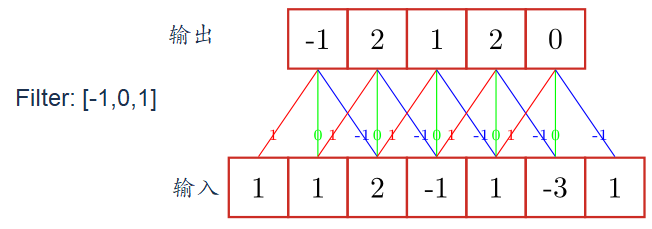
二维卷积

卷积也经常用在图像处理中。因为图像为一个两维结构，所以需要将一维卷积进行扩展。给定一个图像 \(X \in \mathbb{R}^{M \times N}\)，和滤波器 \(W \in \mathbb{R}^{m \times n}\) 一般 \(m<<M, n<<N\) ，其卷积为：

\[y_{i j}=\sum_{u=1}^{m} \sum_{v=1}^{n} w_{u v} \cdot x_{i-u+1, j-v+1} \]

二维卷积示例

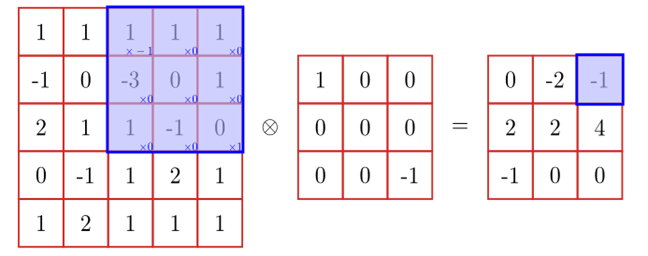
在图像处理中，卷积经常作为特征提取的有效方法。一幅图像在经过卷积操作后得到结果称为 特征映射（Feature Map）。

图像卷积示例

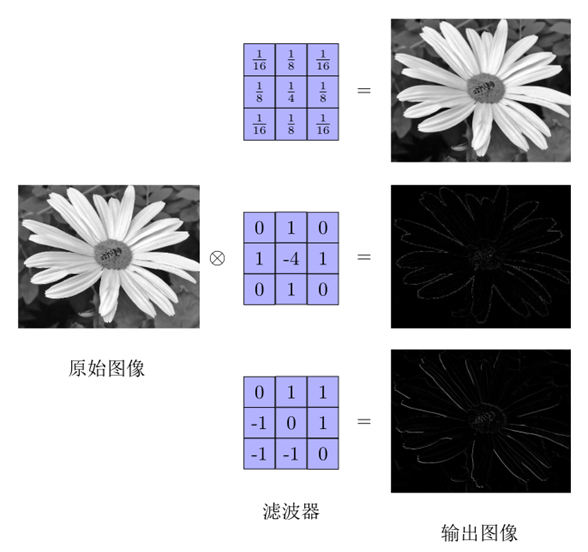
最上面的滤波器是常用的高斯滤波器，可以用来对图像进行平滑去噪；中间和最下面的过滤器可以用来提取边缘特征。

互相关

在机器学习和图像处理领域，卷积的主要功能是在一个图像（或某种特征）上滑动一个卷积核（即滤波器），通过卷积操作得到一组新的特征。在计算卷积的过程中，需要进行卷积核翻转。在具体实现上，一般会以互相关操作来代替卷积，从而会减少一些不必要的操作或开销。
互相关（Cross-Correlation）是一个衡量两个序列相关性的函数，通常是用滑动窗口的点积计算来实现。
给定一个图像 \(X \in \mathbb{R}^{M \times N}\)，和滤波器 \(W \in \mathbb{R}^{m \times n}\)，它们的互相关为：

\[y_{i j}=\sum_{u=1}^{m} \sum_{v=1}^{n} w_{u v} \cdot x_{i+u-1, j+v-1} \]

上面的式子可以表示为：

\[Y=W \otimes X \]

其中 \(Y \in \mathbb{R}^{M-m+1, N-n+1}\) 为输出矩阵。

互相关的计算过程如下图所示：

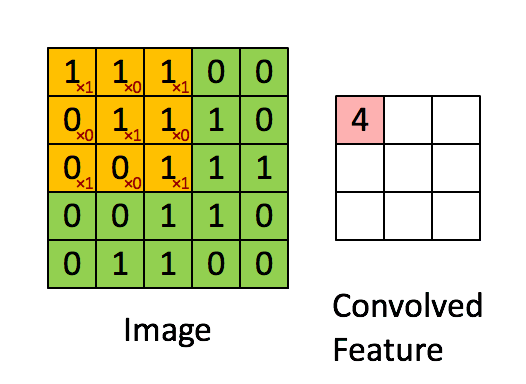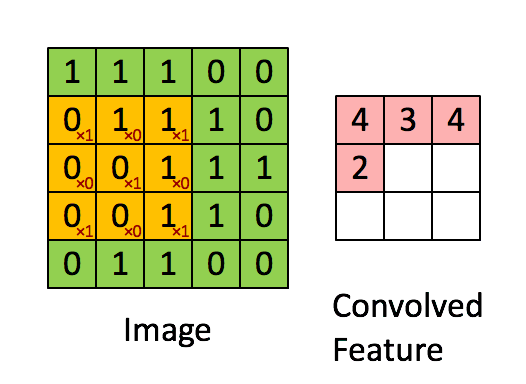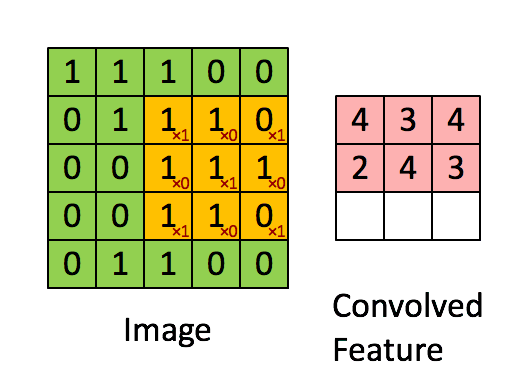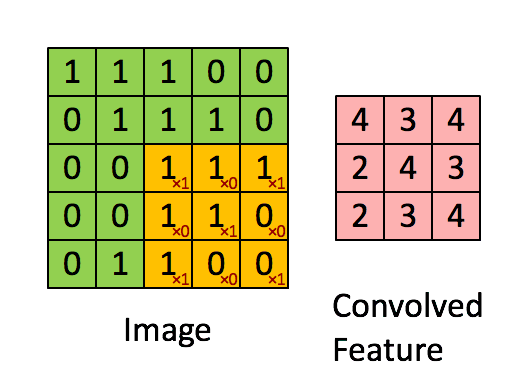
互相关与卷积

互相关和卷积的区别在于卷积核是否进行翻转。因此互相关也可以称为不翻转卷积。
在神经网络中使用卷积是为了进行特征抽取，卷积核是否进行翻转和其特征抽取的能力无关。特别是当卷积核是可学习的参数时，卷积和互相关是等价的。
因此，为了实现上（或描述上）的方便起见，我们用互相关来代替卷积。事实上，很多深度学习工具中卷积操作其实都是互相关操作。

卷积的变种

在卷积的标准定义基础上，还可以引入滤波器的滑动步长（Stride）和零填充（Padding）来增加卷积的多样性，可以更灵活地进行特征抽取。
步长为1和步长为2时的结果对比：

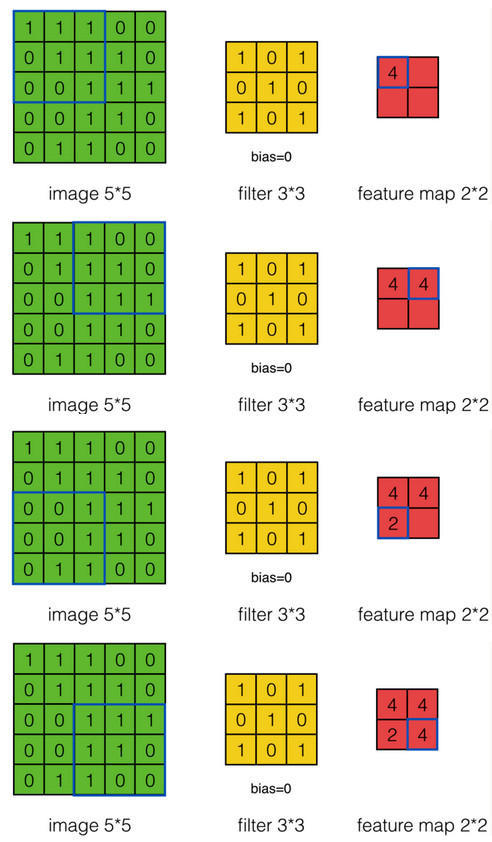
零填充示例：

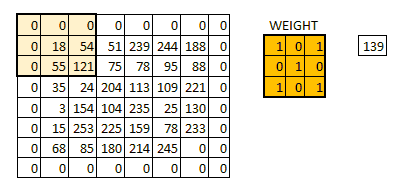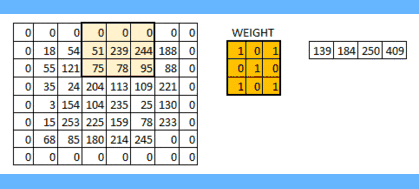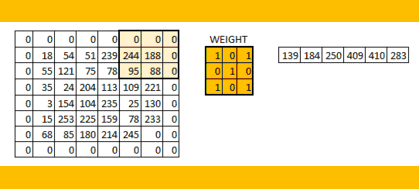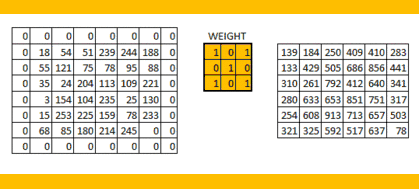
在进行卷积运算时，就存在两种选择：
Valid 卷积：不进行任何处理，直接卷积卷积，得到的Feature Map 将会比原图像的尺寸小。
Same 卷积：进行填充，并使得卷积后结果的大小与原图的一致。
卷积过程中，有时需要通过填充来避免信息损失，有时也要在卷积时通过设置的步长（Stride）来压缩一部分信息。
步长、填充、原始尺寸、卷积后的尺寸、滤波器尺寸之间的关系可以表示为：

\[{W_2} = \left\lfloor {\frac{{{W_1} - F + 2P}}{S} + 1} \right\rfloor \]

\[{H_2} = \left\lfloor {\frac{{{H_1} - F + 2P}}{S} + 1} \right\rfloor \]

其中：
\({{W_1}},{{H_1}}\) 是原来的宽度和高度；
\({{W_2}},{{H_2}}\) 是卷积后的宽度和高度；
\(F\) 是滤波器尺寸；
\(P\) 是填充尺寸；
\(S\) 是步长；
\(\left\lfloor {} \right\rfloor\) 是向下取整符号，用于结果不是整数时进行向下取整。

多核高维卷积

权值的纵深维度（depth dimension）和输入图像的信道(Channel)是相同的。
每一个过滤器的输出被堆叠在一起，形成卷积图像的纵深维度，卷积后Feature Map的深度(个数)和卷积层的filter个数是相同的。

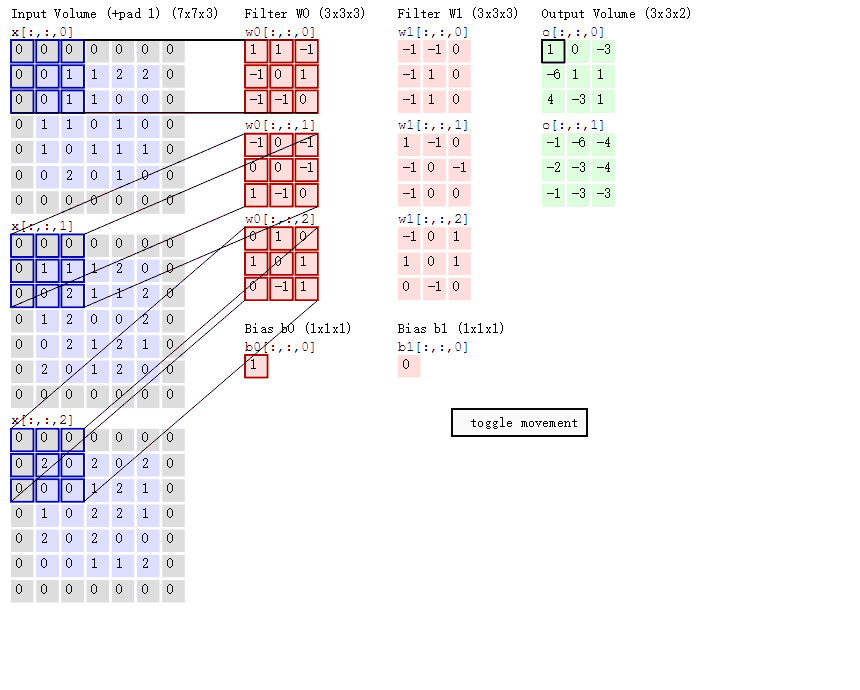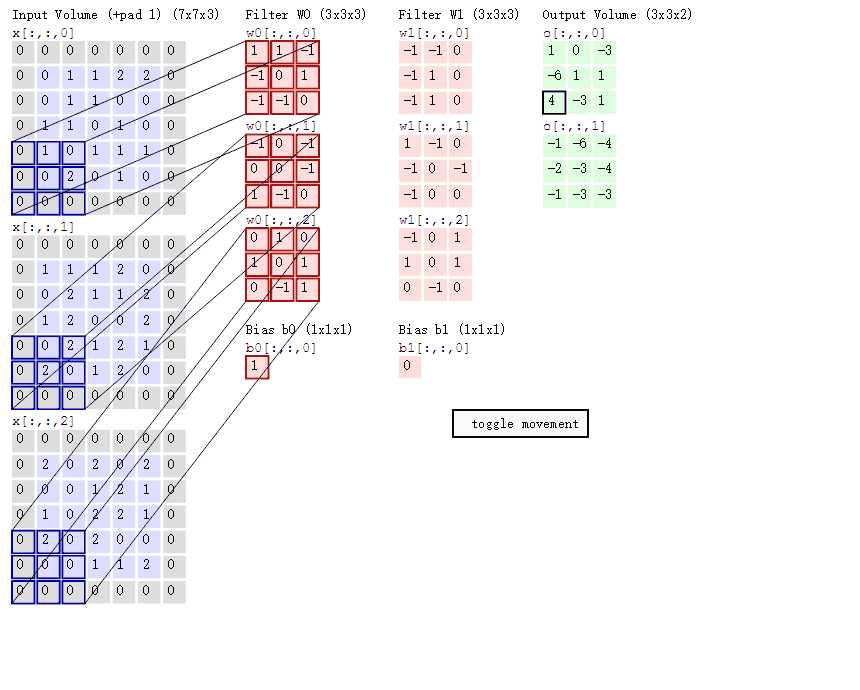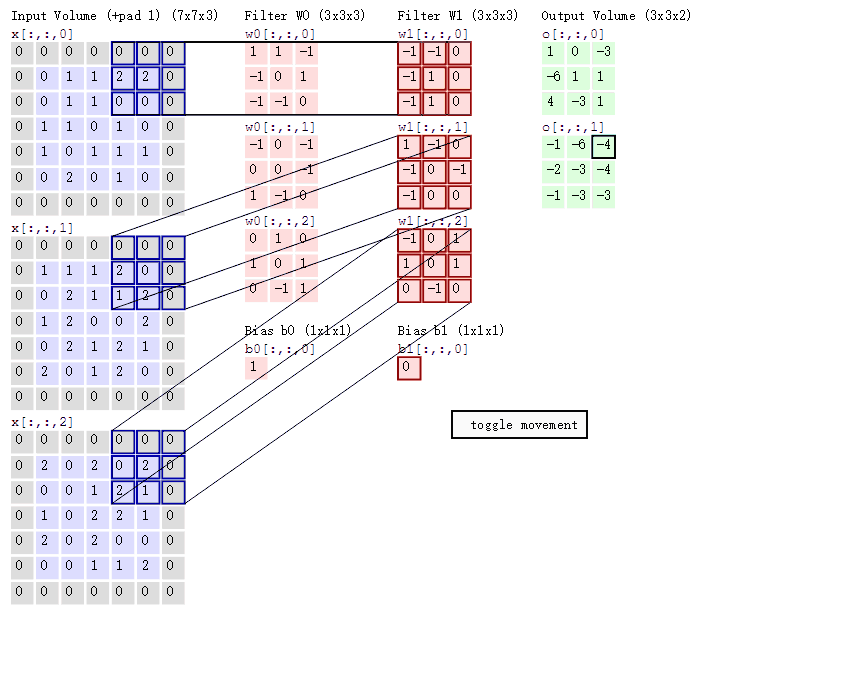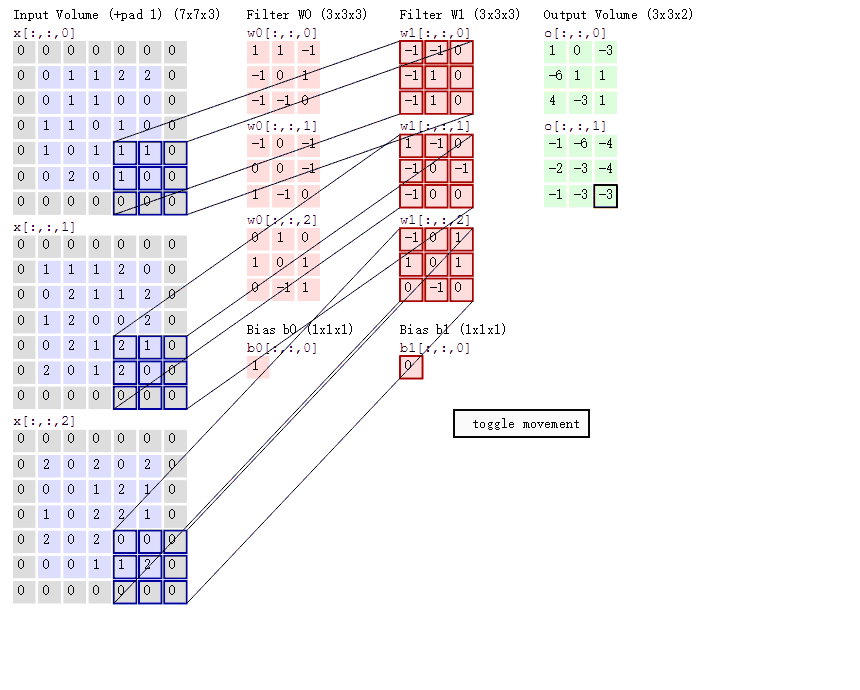
如图：
根据公式计算：

\[\frac{5+2 * 1-3}{2}+1=3 \]

输出尺寸为 \(3 \times 3\)；
使用了两个不同的卷积核 \(W_{1}\)、\(W_{2}\)，最终输出 \(13 \times 3 \times 2\)；
计算的过程是将矩阵与滤波器对应的每一信道进行卷积运算，最后相加，得到的结果是一个单信道的矩阵。
另外，三层滤波器中，每一层中的值可以根据需求来设定以达到检测不同特征的目的。