ResNets

ResNets

当一个神经网络某个深度时，将会出现梯度消失（Vanishing Gradient）和梯度爆炸（Exploding Gradient）等问题。而ResNets能很好得解决这些问题。
ResNets全称为残差网络（Residual Networks)，它是微软研究院2015年在论文中提出的卷积网络。

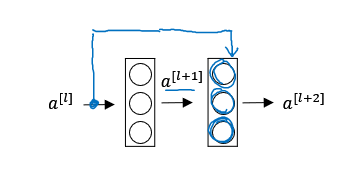
如上图是一个神经网络中的几层，它一般的前向传播的过程，也称为“主要路径（main path）”为：

\[ z^{[l+1]} = W^{[l+1]}a^{[l]} + b^{[l+1]} \]

\[a^{[l+1]} = g(z^{[l+1]}) \]

\[z^{[l+2]} = W^{[l+2]}a^{[l+1]} + b^{[l+2]} \]

\[a^{[l+2]} = g(z^{[l+2]}) \]

在残差网络中，通过“捷径（short cut）”直接把\(a^{[l]}\)添加到第二个ReLu过程里，也就是最后的计算过程中：

\[a^{[l+2]} = g(z^{[l+2]} + W_s a^{[l]}) \]

其中\(a^{[l]}\)需要乘以一个矩阵\(W_s\)使得它的大小和\(z^{[l+2]}\)匹配。
深度神经网络通过这种跳跃网络层的方式能获得更好的训练效果。上面这种结构被称为一个残差块（Residual Blocks）。

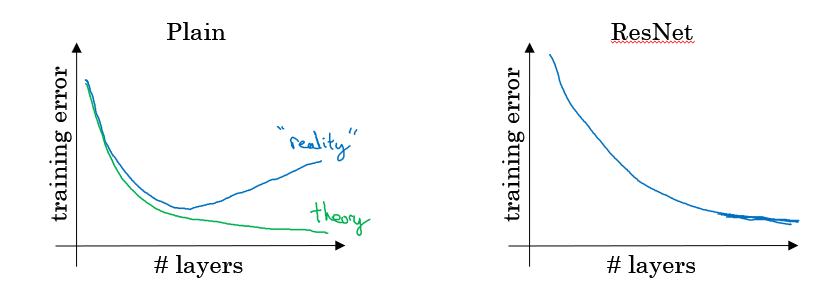
普通的神经网络随着梯度下降的进行，理论上成本是不断下降的，而实际上当神经网络达到一定的深度时，成本值降低到一定程度后又会趋于上升，残差神经网络则能解决这个问题。
对于一个神经网络中存在的一些恒等函数（Identity Function），残差网络在不影响这个神经网络的整体性能下，使得对这些恒等函数的学习更加容易，而且很多时候还能提高整体的学习效率。