卷积神经网络

用卷积来代替全连接

在全连接前馈神经网络中，如果第 \(l\) 层有 \(n^{l}\) 个神经元，第 \(l-1\) 层有 \(n^{(l-1)}\) 个神经元，连接边有 \(n^{(l)} \times n^{(l-1)}\) ，也就是权重矩阵有 \(n^{(l)} \times n^{(l-1)}\) 个参数。当 \(m\) 和 \(n\) 都很大时，权重矩阵的参数非常多，训练的效率会非常低

如果采用卷积来代替全连接，第 \(l\) 层的净输入 \(\mathbf{z}^{(l)}\) 为第 \(l-1\) 层活性值 \(\mathbf{a}^{(l-1)}\) 和滤波器 \(\mathbf{w}^{(l)} \in \mathbb{R}^{m}\) 的卷积，即：

\[\mathbf{z}^{(l)}=\mathbf{w}^{(l)} \otimes \mathbf{a}^{(l-1)}+b^{(l)} \]

其中滤波器 \(\mathbf{w}^{(l)}\) 为可学习的权重向量，\(b^{(l)} \in \mathbb{R}^{n^{l-1}}\) 为可学习的偏置。
根据卷积的定义，卷积层有两个很重要的性质：
局部连接
在卷积层（假设是第 \(l\) 层）中的每一个神经元都只和下一层（第 \(l − 1\) 层）中某个局部窗口内的神经元相连，构成一个局部连接网络。卷积层和下一层之间的连接数大大减少，有原来的 \(n^{l} \times n^{l-1}\) 个连接变为 \(n^{l} \times m\) 个连接， \(m\) 为滤波器大小。

权值共享
作为参数的滤波器 w(l) 对于第 l 层的所有的神经元都是相同的。

由于局部连接和权重共享，卷积层的参数只有一个 \(m\) 维的权重 \(\mathbf{w}^{(l)}\) 和 1维的偏置 \(b^{(l)}\)，共 \(m + 1\) 个参数，参数个数和神经元的数量无关。
此外，第 \(l\) 层的神经元个数不是任意选择的，而是满足 \(n^{(l)}=n^{(l-1)}-m+1\)。

卷积层

卷积层的作用是提取一个局部区域的特征，不同的卷积核相当于不同的特征提取器。
为了更充分地利用图像的局部信息，通常将神经元组织为三维结构的神经层，其大小为高度 \(M\) × 宽度 \(N\) × 深度 \(D\)，有 \(D\) 个 \(M × N\) 大小的特征映射构成。

特征映射（Feature Map）为一幅图像（或其它特征映射）在经过卷积提取到的特征，每个特征映射可以作为一类抽取的图像特征。为了提高卷积网络的表示能力，可以在每一层使用多个不同的特征映射，以更好地表示图像的特征。

在输入层，特征映射就是图像本身。如果是灰度图像，就是有一个特征映射，深度 \(D = 1\)；如果是彩色图像，分别有 RGB三个颜色通道的特征映射，输入层深度 \(D = 3\)。

• 输入特征映射组：\(\mathbf{X} \in \mathbb{R}^{M \times N \times D}\) 为三维张量（tensor），其中每个切片(slice)矩阵 \(X^{d} \in \mathbb{R}^{M \times N}\) 为一个输入特征映射， \(1 \leq d \leq D\)；
• 输出特征映射组： \(\mathbf{Y} \in \mathbb{R}^{M^{\prime} \times N^{\prime} \times P}\) 为三维张量，其中每个切片矩阵\(Y^{p} \in{R}^{M^{\prime}} \times N^{\prime}\)为一个输出特征映射，\(1 \leq p \leq P\)。
• 卷积核： \(\mathbf{W} \in \mathbb{R}^{m \times n \times D \times P}\) 为四维张量，其中每个切片矩阵 \(W^{p, d} \in \mathbb{R}^{m \times n}\)为一个两维卷积核， \(1 \leq d \leq D, 1 \leq p \leq P\)

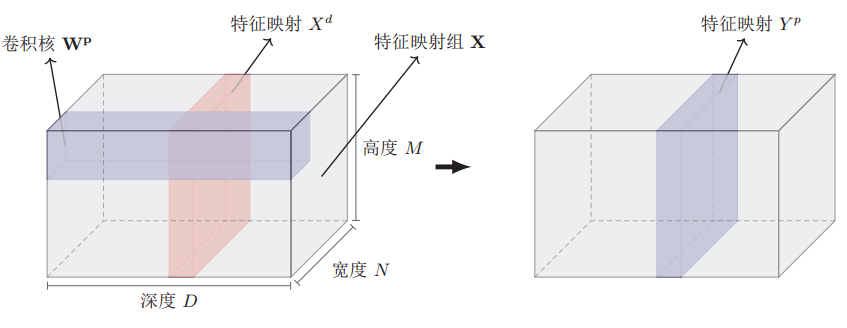
为了计算输出特征映射 \(Y^{p}\)，用卷积核 \(W^{p, 1}, W^{p, 2}, \cdots, W^{p, D}\) 分别对输入特征映射 \(X^{1}, X^{2}, \cdots, X^{D}\) 进行卷积，然后将卷积结果相加，并加上一个标量偏置 \(b\) 得到卷积层的净输入 \(Z P\) ，再经过非线性激活函数后得到输出特征映射 \(Y P\)。

\[\begin{aligned} Z^{p} &=\mathbf{W}^{p} \otimes \mathbf{X}+b^{p}=\sum_{d=1}^{D} W^{p, d} \otimes X^{d}+b^{p} \\ Y^{p} &=f\left(Z^{p}\right) \end{aligned} \]

其中 \(\mathbf{W}^{p} \in \mathbb{R}^{m \times n \times D}\) 为三维卷积核，\(f(\cdot)\) 为非线性激活函数，一般用 ReLU函数。整个计算过程如图：

在输入为 \(\mathbf{X} \in \mathbb{R}^{M \times N \times D}\) ，输出为 \(\mathbf{Y} \in \mathbb{R}^{M^{\prime} \times N^{\prime} \times P}\) 的卷积层中，每一个输入特征映射都需要 \(D\) 个滤波器以及一个偏置。假设每个滤波器的大小为 \(m \times n\) 那么共需要 \(P \times D \times(m \times n)+P\) 个参数。

池化层

池化层（Pooling Layer）也叫子采样层（Subsampling Layer），其作用是进行特征选择，降低特征数量，并从而减少参数数量。

卷积层虽然可以显著减少网络中连接的数量，但特征映射组中的神经元个数并没有显著减少。如果后面接一个分类器，分类器的输入维数依然很高，很容易出现过拟合。为了解决这个问题，可以在卷积层之后加上一个池化层，从而降低特征维数，避免过拟合。
池化(Pooling) 是指对每个区域进行下采样（Down Sampling）得到一个值，作为这个区域的概括。
常用的池化函数有两种：

1. 最大池化（Maximum Pooling）：一般是取一个区域内所有神经元的最大值。

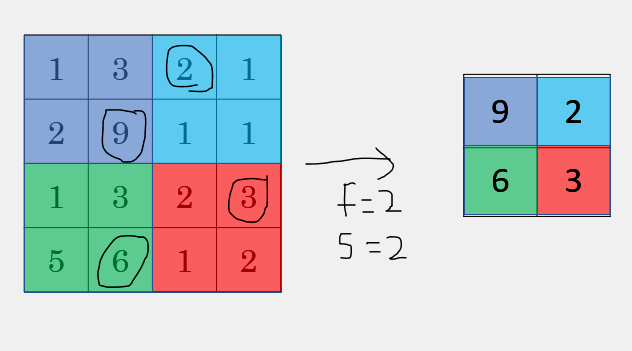
2. 平均池化（Mean Pooling）：一般是取区域内所有神经元的平均值。
   

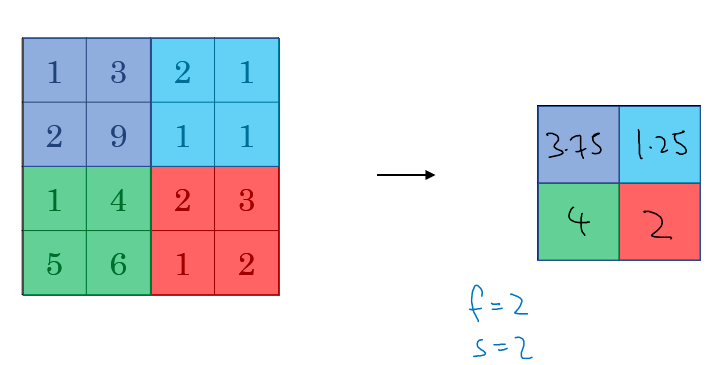
最大池化操作的示例：

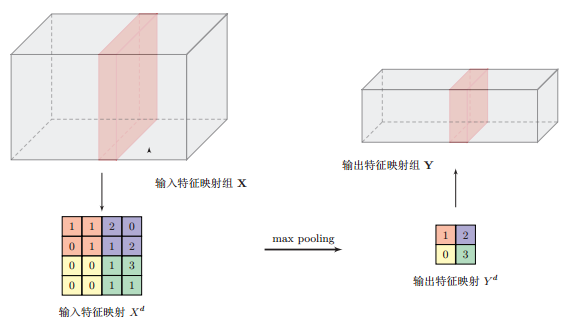
目前主流的卷积网络中，池化层仅包含下采样操作。但在早期的一些卷积网络（比如 LeNet-5）中，有时也会在池化层使用非线性激活函数，比如：

\[Y^{\prime d}=f\left(w^{d} \cdot Y^{d}+b^{d}\right) \]

其中 \(Y^{\prime d}\) 为汇聚层的输出， \(f(\cdot)\) 为非线性激活函数， \(w^{d}\) 和 \(b^{d}\) 为可学习的标量权重和偏置。

典型的汇聚层是将每个特征映射划分为 \(2 \times 2\) 大小的不重叠区域，然后使用最大汇聚的方式进行下采样。汇聚层也可以看做是一个特殊的卷积层，卷积核大小为 \(m \times m\)，步长为 \(\boldsymbol{S} \times \boldsymbol{S}\)，卷积核为 max函数或 mean函数。过大的采样区域会急剧减少神经元的数量，会造成过多的信息损失。

全连接网络和卷积网络

全连接神经网络之所以不太适合图像识别任务，主要有以下几个方面的问题：

1. 参数数量太多
   考虑一个输入10001000像素的图片(一百万像素，现在已经不能算大图了)，输入层有10001000=100万节点。假设第一个隐藏层有100个节点(这个数量并不多)，那么仅这一层就有(10001000+1)100=1亿参数，这实在是太多了！我们看到图像只扩大一点，参数数量就会多很多，因此它的扩展性很差。

2. 没有利用像素之间的位置信息
   对于图像识别任务来说，每个像素和其周围像素的联系是比较紧密的，和离得很远的像素的联系可能就很小了。如果一个神经元和上一层所有神经元相连，那么就相当于对于一个像素来说，把图像的所有像素都等同看待，这不符合前面的假设。当我们完成每个连接权重的学习之后，最终可能会发现，有大量的权重，它们的值都是很小的(也就是这些连接其实无关紧要)。努力学习大量并不重要的权重，这样的学习必将是非常低效的。

3. 网络层数限制
   我们知道网络层数越多其表达能力越强，但是通过梯度下降方法训练深度全连接神经网络很困难，因为全连接神经网络的梯度很难传递超过3层。因此，我们不可能得到一个很深的全连接神经网络，也就限制了它的能力。

卷积神经网络解决上述问题的思路：

1. 局部连接：这个是最容易想到的，每个神经元不再和上一层的所有神经元相连，而只和一小部分神经元相连。这样就减少了很多参数。
2. 权值共享：一组连接可以共享同一个权重，而不是每个连接有一个不同的权重，这样又减少了很多参数。
3. 下采样：可以使用Pooling来减少每层的样本数，进一步减少参数数量，同时还可以提升模型的鲁棒性。

典型的卷积网络结构

通常一个卷积神经网络是由输入层（Input）、卷积层（Convolution）、池化层（Pooling）、全连接层（Fully Connected）组成。
目前常用的卷积网络结构如图所示：

一个卷积块为连续 \(M\) 个卷积层和 \(b\) 个池化层（\(M\) 通常设置为 2 ∼ 5，\(b\) 为 0或 1）。一个卷积网络中可以堆叠\(N\) 个连续的卷积块，然后在接着 \(K\) 个全连接层（\(N\) 的取值区间比较大，比如 1 ∼ 100或者更大； \(K\)一般为0 ∼ 2）。

目前，整个网络结构趋向于使用更小的卷积核（比如 1 × 1和 3 × 3）以及更深的结构（比如层数大于 50）。此外，由于卷积的操作性越来越灵活（比如不同的步长），池化层的作用变得也越来越小，因此目前比较流行的卷积网络中，池化层的比例也逐渐降低，趋向于全卷积网络。