批标准化

批标准化

批标准化（Batch Normalization，BN）和之前的数据集标准化类似，是将分散的数据进行统一的一种做法。具有统一规格的数据，能让机器更容易学习到数据中的规律。
对于含有m个节点的某一层神经网络，对z进行操作的步骤为：

\[\mu = \frac{1}{m} \sum_{i=1}^m z^{(i)} \]

\[\sigma^2 = \frac{1}{m} \sum_{i=1}^m (z^{(i)}-\mu)^2 \]

\[z_{norm}^{(i)} = \frac{{{z^{(i)}} - \mu }}{{\sqrt {{\delta ^2} + \varepsilon } }} \]

\[\tilde{z}^{(i)} = \gamma z_{norm}^{(i)}+\beta \]

其中的\(\gamma\)、\(\beta\)并不是超参数，而是两个需要学习的参数，神经网络自己去学着使用和修改这两个扩展参数。这样神经网络就能自己慢慢琢磨出前面的标准化操作到底有没有起到优化的作用。如果没有起到作用，就使用 \(\gamma\)和\(\beta\)来抵消一些之前进行过的标准化的操作。
例如当\(\gamma = \sqrt{\sigma^2+\epsilon}, \beta = \mu\)，就抵消掉了之前的正则化操作。
Batch 归一化的作用是它适用的归一化过程，不只是输入层，甚至同样适用于神经网络中的深度隐藏层。应用 Batch 归一化了一些隐藏单元值中的平均值和方差，不过训练输入和这些隐藏单元值的一个区别是，你也许不想隐藏单元值必须是平均值 0 和方差 1。\(\gamma\)、\(\beta\)参数控制使得均值和方差可以是 0 和 1，也可以是其它值。

可以认为每个圆圈代表着两步计算，先计算z，再计算a。
如果没有Batch Norm，那么计算步骤就是根据输入\(X\)，\({\omega ^{[1]}}\)，\({b^{[1]}}\)计算出\({z^{[1]}}\)，再利用激活函数计算出\({a^{[1]}}\)，以此类推计算出\({z^{[2]}}\)，\({a^{[2]}}\)。
Batch归一化的做法是先将\({z^{[1]}}\)值进行Batch归一化，简称BN，此过程由参数\({\beta ^{[1]}}\)，\({\gamma ^{[1]}}\)控制的，这一操作的结果为\(\tilde{z}^{[1]}\) ，然后将其输入激活函数中得到\({a^{[1]}}\)，即：

\[{a^{[1]}} = {g^{[1]}}({{\tilde z}^{[1]}}) \]

依次类推：

\[{a^{[2]}} = {g^{[2]}}({{\tilde z}^{[2]}}) \]

Batch 归一化是发生在计算z和a之间的，除了参数\({w^{[l]}}\)，\({b^{[l]}}\)又加入了新的参数\({\beta ^{[l]}}\)和\({\gamma ^{[l]}}\)。
接下来可以使用任意一种优化算法，例如梯度下降算法：

\[{\beta ^{[l]}} = {\beta ^{[l]}} - \alpha d{\beta ^{[l]}} \]

当然也可以使用 Adam 或 RMSprop 或 Momentum来进行参数更新。
实践中， Batch 归一化通常和训练集的 mini-batch 一起使用。

Batch Norm的作用

在猫识别的问题上，假设训练集中只包含黑猫的识别，其训练集以及正负样本分布如下图所示：

现在要将训练的结果使用在带颜色的猫识别问题中，其样本和正负分布可能如下图所示：

此时在识别黑猫中训练很好的模块可能并不会在在识别带颜色猫的问题上表现的依旧很好。这种数据分布改变的问题称为 “Covariate shift”，具体可以理解为：
已经学习到了x到y的映射，但是如果x的分布改变了，那么可能需要重新训练学习算法。
“Covariate shift”问题在神经网络中的体现，如下的神经网络：

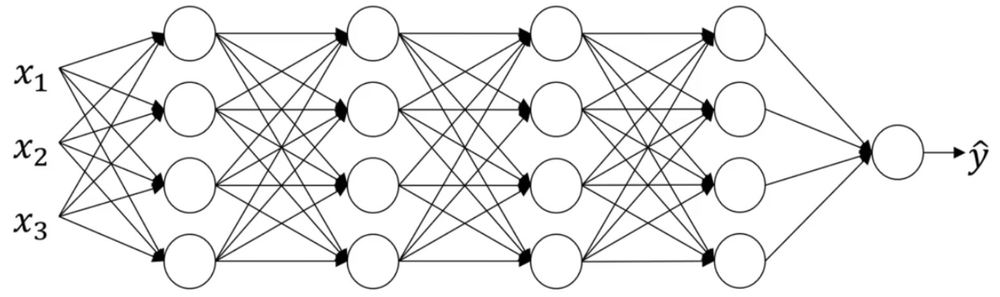
我们从第三层开始看起，遮挡住前两层：

从第三隐藏层的角度来看，它得到一些值，称为\(a_1^{[2]}\)，\(a_2^{[2]}\)，\(a_3^{[2]}\)，\(a_4^{[2]}\)，接下来使用的参数可能是\({w^{[3]}}\)，\({b^{[3]}}\)，\({w^{[4]}}\)，\({b^{[4]}}\)，从而最终得到不错的映射\({\hat y}\)。
现在将前两层的遮挡去掉：

可以看到这个网络还有参数\({w^{[1]}}\)，\({b^{[1]}}\)，\({w^{[2]}}\)，\({b^{[2]}}\)，如果这些参数改变了，那么\({a^{\left[ 2 \right]}}\)的值也会改变。所以从第三层隐藏层的角度来看，这些隐藏单元的值在不断地改变， 所以它就有了“Covariate shift”的问题。

Batch 归一化做的，是它减少了这些隐藏值分布变化的数量。当神经网络在之前层中更新参数，z的值可能发生变化， Batch 归一化可以确保无论其怎样变化z的均值和方差保持不变，这就使得后面的数据及数据分布更加稳定，减少了前面层与后面层的耦合，使得每一层不过多依赖前面的网络层，最终加快整个神经网络的训练。

Batch 归一化还有一个作用，它有轻微的正则化效果， Batch 归一化中非直观的一件事是在mini-batch计算中，由均值和方差缩放的，因为在mini-batch上计算的均值和方差，而不是在整个数据集上，均值和方差有一些小的噪声。缩放过程从 \({z^{[l]}}\) 到 \({{\tilde z}^{[l]}}\) 的过程中也有一些噪音，因为它是用有些噪音的均值和方差计算得出的。这迫使后部单元不过分依赖任何一个隐藏单元，类似于 dropout，它给隐藏层增加了噪音，因此有轻微的正则化效果。因为添加的噪音很微小，所以并不是巨大的正则化效果，你可以将 Batch 归一化和 dropout 一起使用，如果你想得到 dropout 更强大的正则化效果。

在训练时 \(\mu\) 和 \({\sigma ^2}\) 是在整个mini-batch上计算出来的，但在测试时，你可能需要逐一处理样本。理论上你可以在最终的网络中运行整个训练集来得到\(\mu\) 和 \({\sigma ^2}\) 但在实际操作中，我们通常运用指数加权平均（也叫做流动平均）来追踪在训练过程中你看到的 \(\mu\) 和 \({\sigma ^2}\) 。

我们选择\(l\)层，假设我们有mini-batch：\({{\rm{X}}^{[1]}}\)，\({{\rm{X}}^{[2]}}\)，\({{\rm{X}}^{[3]}}\)......以及对应的\(y\)值等等。
第一个mini-batch \({{\rm{X}}^{\{ 1\} }}\)的第\(l\)层训练时得到了\({\mu ^{\{ 1\} \{ l\} }}\)；
第二个mini-batch \({{\rm{X}}^{\{ 1\} }}\)的第\(l\)层训练时得到了\({\mu ^{\{ 2\} \{ l\} }}\)；
第三个mini-batch \({{\rm{X}}^{\{ 1\} }}\)的第\(l\)层训练时得到了\({\mu ^{\{ 3\} \{ l\} }}\)；
这样在计算每个batch的\(l\)层$\mu \(和\){\sigma ^2}\(时候，可以采用指数加权平均的方法可以得到这一层\)\mu \(和\){\sigma ^2}\(的实时数值。 最终测试时，使用\)\mu \(和\){\sigma ^2}$的加权平均以及z值计算：

\[z_{norm}^{(i)} = \frac{{{z^{(i)}} - u}}{{\sqrt {{\sigma ^2} + \varepsilon } }} \]

进而计算：

\[{{\tilde z}^{(i)}} = \gamma z_{norm}^{(i)} + \beta \]