梯度下降算法优化

指数加权平均

指数加权平均（Exponentially Weight Average）是一种常用的序列数据处理方式，其计算公式为:

\[S_t = \begin{cases} Y_1, & t=1 \\ \beta S_{t-1} + (1-\beta)Y_{t}, & t>1 \end{cases} \]

其中\(Y_t\)为\(t\)下的实际值，\(S_t\)为\(t\)下加权平均后的值，\(β\)为权重值。
给定一个时间序列，例如伦敦一年每天的气温值：

如果要计算趋势的话，也就是温度的局部平均值，或者说移动平均值，先使：

\[{v_0} = 0 \]

然后计算：

\[{v_1} = 0.9{v_0} + 0.1{\theta _1} \]

\[{v_2} = 0.9{v_1} + 0.1{\theta _2} \]

依次类推：

\[{v_t} = 0.9{v_{t - 1}} + 0.1{\theta _t} \]

实际上：

\[v_{100} = 0.1\theta_{100}+0.1 \times 0.9\theta_{99} +0.1 \times 0.9^2\theta_{98} \ … \]

第 100 天计算的数据是一个总和，包括100号数据，99号数据，98号数据等等。
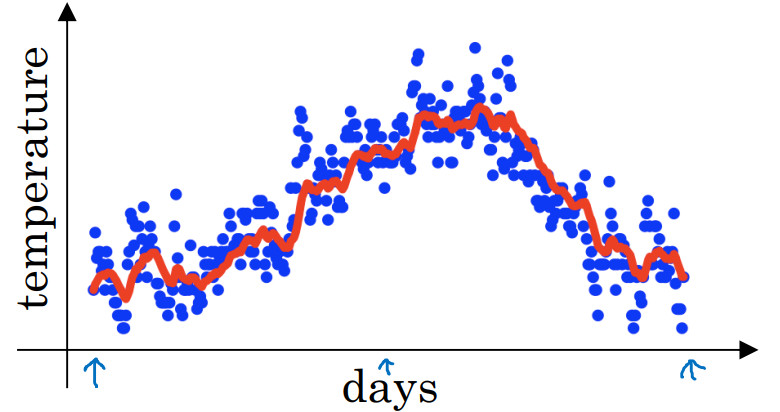
将移动平均值即每日温度的指数加权平均值画出来的效果是：

上面的计算更一般的形式是：

\[{v_t} = \beta {v_{t - 1}} + (1 - \beta ){\theta _t} \]

\({v_t}\)可以理解为大概是\(\frac{1}{{(1 - \beta )}}\)的平均温度，例如：\(\beta = 0.9\)，可以理解为这是十天的平均值，也就是上图红线部分，它反应了温度变化的大致趋势。

• 当取权重值\(\beta=0.98\)时，大概计算过去 50 天的温度，可以得到图中更为平滑的绿色曲线。
• 当取权重值\(\beta=0.5\)时，大概计算过去 2天的温度，得到图中噪点更多的黄色曲线。

\(\beta\)越大相当于求取平均利用的天数就越多，曲线自然就会越平滑而且越滞后。

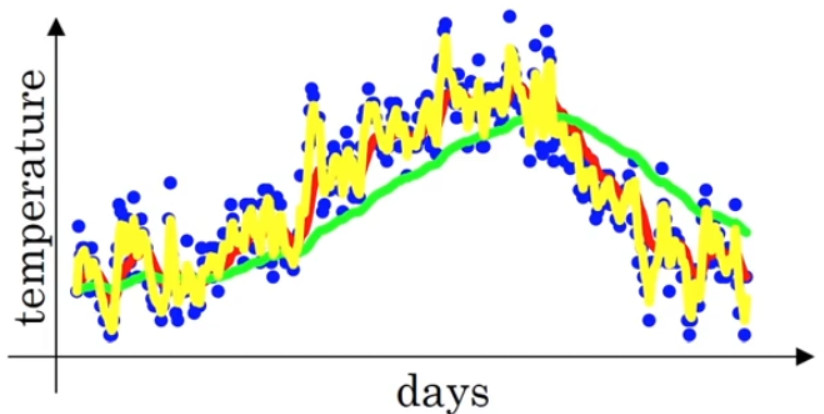
实际上\(\beta {\rm{ = }}0.98\)时，图中所示的划线并不是绿色的线，而是下图紫色的线条：

当进行指数加权平均计算时，第一个值\(v_o\)被初始化为0，这样将在前期的运算用产生一定的偏差。为了矫正偏差，需要在每一次迭代后用以下式子进行偏差修正：

\[v_t := \frac{v_t}{1-\beta^t} \]

举个具体例子：
当\(t = 2\)时：
\(\frac{{{v_2}}}{{1 - {\beta ^2}}} = \frac{{0.0196{\theta _1} + 0.02{\theta _2}}}{{1 - {{0.98}^2}}} = \frac{{0.0196{\theta _1} + 0.02{\theta _2}}}{{0.0396}}\)
也就是\({\theta _1}，{\theta _2}\)的加权平均数，并去除偏差。
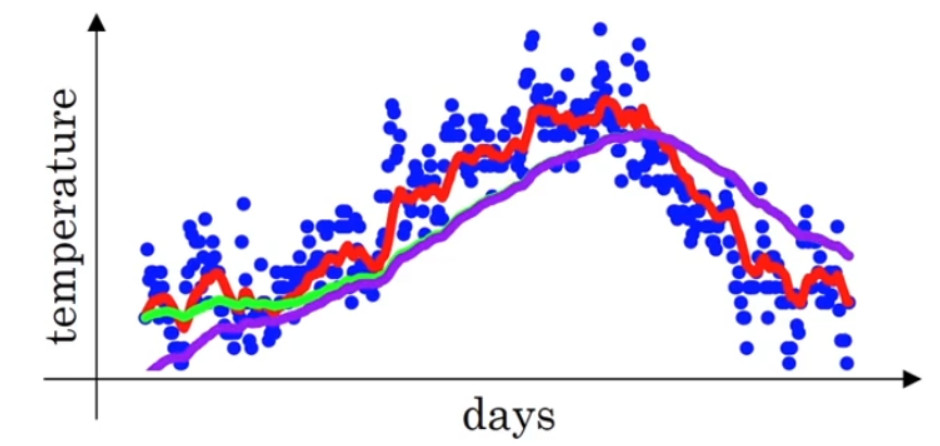
随着\(t\)增加，\({{\beta ^t}}\)接近于 0，所以当\(t\)很大的时候，偏差修正几乎没有作用，因此当\(t\)较大的时候，紫线基本和绿线重合了。不过在开始学习阶段，你才开始预测热身练习，偏差修正可以帮助你更好预测温度，偏差修正可以帮助你使结果从紫线变成绿线。
在机器学习中，在计算指数加权平均数的大部分时候，大家不在乎执行偏差修正，因为大部分人宁愿熬过初始时期，拿到具有偏差的估测，然后继续计算下去。如果你关心初始时期的偏差，在刚开始计算指数加权移动平均数的时候，偏差修正能帮助你在早期获取更好的估测。

Momentum梯度下降

动量梯度下降（Gradient Descent with Momentum）是计算梯度的指数加权平均数，并利用该值来更新参数值。
动量梯度下降法运行速度几乎总是快于标准的梯度下降算法。
具体过程为：

\[v_{dw} = \beta v_{dw} + (1-\beta)dw \]

\[v_{db} = \beta v_{db} + (1-\beta)db \]

\[w := w-\alpha v_{dw} \]

\[b := b-\alpha v_{db} \]

其中的动量衰减参数\(β\)一般取0.9。

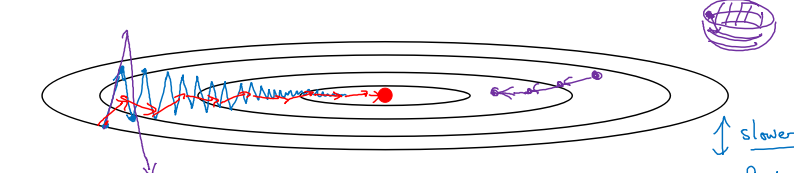
进行一般的梯度下降将会得到图中的蓝色曲线，而使用Momentum梯度下降时，通过累加减少了抵达最小值路径上的摆动，加快了收敛，得到图中红色的曲线。
当前后梯度方向一致时，Momentum梯度下降能够加速学习；前后梯度方向不一致时,Momentum梯度下降能够抑制震荡。

RMSProp算法

RMSProp(Root Mean Square Prop，均方根支)算法在对梯度进行指数加权平均的基础上，引入平方和平方根。具体过程为：

\[s_{dw} = \beta s_{dw} + (1-\beta)dw^2 \]

\[s_{db} = \beta s_{db} + (1-\beta)db^2 \]

\[w := w-\alpha \frac{dw}{\sqrt{s_{dw}+\epsilon}} \]

\[b := b-\alpha \frac{db}{\sqrt{s_{db}+\epsilon}} \]

其中的\(\epsilon=10^{-8}\)，用以提高数值稳定度，防止分母太小。
当\(dw\)或\(db\)较大时，\(dw^{2}\)、\(db^{2}\)会较大，造成\(s_{dw}\)、 \(s_{db}\)也会较大，最终使\(\frac{dw}{\sqrt{s_{dw}}}\)、\(\frac{db}{\sqrt{s_{db}}}\)较小，减小了抵达最小值路径上的摆动。

使用RMSprop 的影响就是你的更新最后会变成这样（绿色线），纵轴方向上摆动较小，而横轴方向继续推进。
还有个影响就是，你可以用一个更大学习率a，然后加快学习，而无须在纵轴上垂直方向偏离。

Adam优化算法

Adam(Adaptive Moment Estimation，自适应矩估计)优化算法适用于很多不同的深度学习网络结构，它本质上是将Momentum梯度下降和RMSProp算法结合起来。具体过程为：

\[v_{dw} = \beta_1 v_{dw} + (1-\beta_1)dw, \ v_{db} = \beta_1 v_{db} + (1-\beta_1)db \]

\[s_{dw} = \beta_2 s_{dw} + (1-\beta_2)dw^2,\ s_{db} = \beta_2 s_{db} + (1-\beta_2)db^2 \]

\[v^{corrected}_{dw} = \frac{v_{dw}}{(1-\beta_1^t)},\ v^{corrected}_{db} = \frac{v_{db}}{(1-\beta_1^t)} \]

\[s^{corrected}_{dw} = \frac{s_{dw}}{(1-\beta_2^t)},\ s^{corrected}_{db} = \frac{s_{db}}{(1-\beta_2^t)} \]

\[w := w-\alpha \frac{v^{corrected}_{dw}}{\sqrt{s^{corrected}_{dw}}+\epsilon} \]

\[b := b-\alpha \frac{v^{corrected}_{db}}{\sqrt{s^{corrected}_{db}}+\epsilon} \]

其中的学习率\(α\)需要进行调参，超参数\(β1\)被称为第一阶矩，一般取0.9，\(β2\)被称为第二阶矩，一般取0.999，\(ϵ\)一般取\(10^{−8}\)。