梯度下降法
梯度下降法
批梯度下降法（Batch Gradient Descent，BGD）是最常用的梯度下降形式，前面的Logistic回归及深层神经网络的构建中所用到的梯度下降都是这种形式。其在更新参数时使用所有的样本来进行更新，具体过程为：
\[{X = [x^{(1)},x^{(2)},…,x^{(m)}]}
\]
\[z^{[1]} = w^{[1]}X + b^{[1]}
\]
\[a^{[1]} = g^{[1]}(z^{[1]})
\]
\[... \ ...
\]
\[z^{[l]} = w^{[l]}a^{[l-1]} + b^{[l]}
\]
\[a^{[l]} = g^{[l]}(z^{[l]})
\]
\[{J(\theta) = \frac{1}{m} \sum_{i=1}^m \mathcal{L}({\hat y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \sum\limits_{l=1}^L ||w^{[l]}}||^2_F
\]
\[{\theta_j:= \theta_j -\alpha\frac{\partial J(\theta)}{\partial \theta_j}}
\]
示例图：
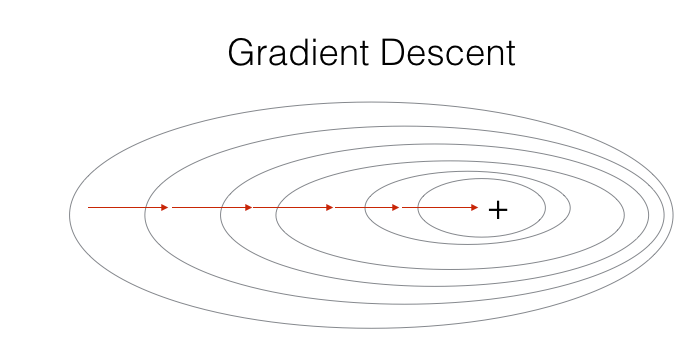
随机梯度下降
随机梯度下降法（Stochastic Gradient Descent，SGD）与批梯度下降原理类似，区别在于每次通过一个样本来迭代更新。其具体过程为：
\[{X = [x^{(1)},x^{(2)},…,x^{(m)}]}
\]
\[for\ \ \ i=1,2,…,m\ \{ \ \ \ \ \ \ \ \ \ \ \ \
\]
\[z^{[1]} = w^{[1]}x^{(i)} + b^{[1]}
\]
\[a^{[1]} = g^{[1]}(z^{[1]})
\]
\[... \ ...
\]
\[z^{[l]} = w^{[l]}a^{[l-1]} + b^{[l]}
\]
\[a^{[l]} = g^{[l]}(z^{[l]})
\]
\[{J(\theta) = \mathcal{L}({\hat y}^{(i)}, y^{(i)}) + \frac{\lambda}{2} \sum\limits_{l=1}^L ||w^{[l]}}||^2_F
\]
\[\theta_j:= \theta_j -\alpha\frac{\partial J(\theta)}{\partial \theta_j} \}
\]
示例图：
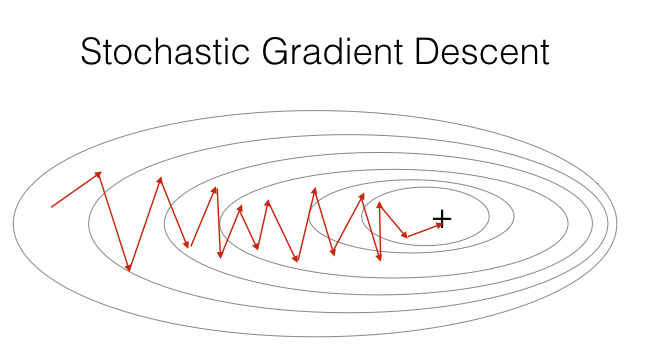
- 优点：训练速度快。
- 缺点：最小化每条样本的损失函数，最终的结果往往是在全局最优解附近，不是全局最优；不易于并行实
小批量梯度下降
小批量梯度下降法（Mini-Batch Gradient Descent，MBGD）是批量梯度下降法和随机梯度下降法的折衷,对用m个训练样本，，每次采用t（1 < t < m）个样本进行迭代更新。具体过程为：
\[{X = [x^{\{1\}},x^{\{2\}},…,x^{\{k = \frac{m}{t}\}}]}
\]
其中：
\[x^{\{1\}} = x^{(1)},x^{(2)},…,x^{(t)}
\]
\[x^{\{2\}} = x^{(t+1)},x^{(t+2)},…,x^{(2t)}
\]
之后：
\[for\ \ \ i=1,2,…,k\ \{ \ \ \ \ \ \ \ \ \ \ \ \
\]
\[z^{[1]} = w^{[1]}x^{\{i\}} + b^{[1]}
\]
\[a^{[1]} = g^{[1]}(z^{[1]})
\]
\[... \ ...
\]
\[z^{[l]} = w^{[l]}a^{[l-1]} + b^{[l]}
\]
\[a^{[l]} = g^{[l]}(z^{[l]})
\]
\[{J(\theta) = \frac{1}{k} \sum_{i=1}^k \mathcal{L}({\hat y}^{(i)}, y^{(i)}) + \frac{\lambda}{2k} \sum\limits_{l=1}^L ||w^{[l]}}||^2_F
\]
\[\theta_j:= \theta_j -\alpha\frac{\partial J(\theta)}{\partial \theta_j} \}
\]
示例图：
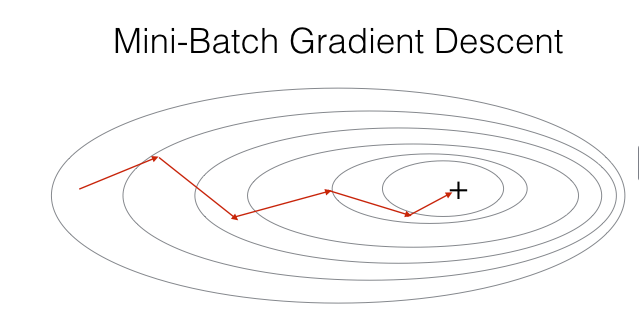
样本数t的值根据实际的样本数量来调整，为了和计算机的信息存储方式相适应，可将t的值设置为2的幂次， 64 到 512 的 mini-batch 比较常见。
将所有的训练样本完整过一遍称为一个epoch。
