前向传播与反向传播
前向传播
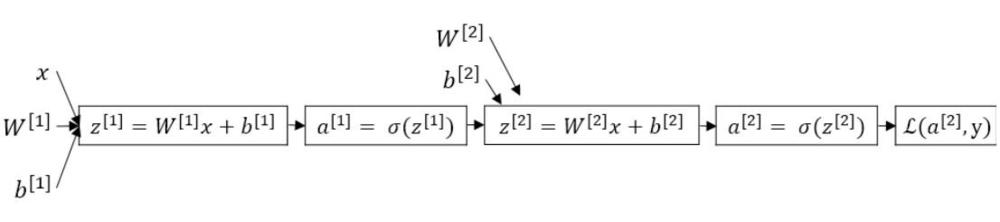
通过输入样本x及参数\(w^{[1]}\)、\(b^{[1]}\)到隐藏层，求得\(z^{[1]}\)，进而求得\(a^{[1]}\);
再将参数\(w^{[2]}\)、\(b^{[2]}\)和\(a^{[1]}\)一起输入输出层求得\(z^{[2]}\)，进而求得\(a^{[2]}\);
最后得到损失函数：\(\mathcal{L}(a^{[2]},y)\)，这样一个从前往后递进传播的过程，就称为前向传播（Forward Propagation）。
前向传播过程中：
\[z^{[1]} = w^{[1]T}X + b^{[1]}
\]
\[a^{[1]} = g(z^{[1]})
\]
\[z^{[2]} = w^{[2]T}a^{[1]} + b^{[2]}
\]
\[a^{[2]} = σ(z^{[2]}) = sigmoid(z^{[2]})
\]
\[{\mathcal{L}(a^{[2]}, y)=-(ylog\ a^{[2]} + (1-y)log(1-a^{[2]}))}
\]
在训练过程中，经过前向传播后得到的最终结果跟训练样本的真实值总是存在一定误差，这个误差便是损失函数。想要减小这个误差，当前应用最广的一个算法便是梯度下降，于是用损失函数，从后往前，依次求各个参数的偏导，这就是所谓的反向传播（Back Propagation），一般简称这种算法为BP算法。
反向传播
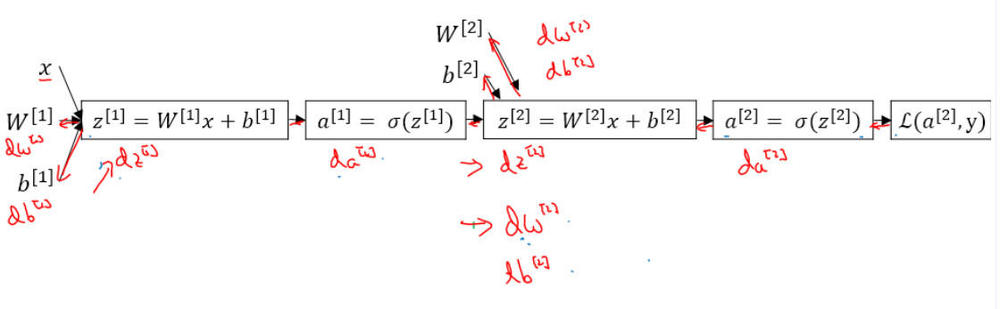
sigmoid函数的导数为：
\[{a^{[2]’} = sigmoid(z^{[2]})’ = \frac{\partial a^{[2]}}{\partial z^{[2]}} = a^{[2]}(1 - a^{[2]})}
\]
由复合函数求导中的链式法则，反向传播过程中：
\[da^{[2]} = \frac{\partial \mathcal{L}(a^{[2]}, y)}{\partial a^{[2]}} = -\frac{y}{a^{[2]}} + \frac{1 - y}{1 - a^{[2]}}
\]
\[dz^{[2]} = \frac{\partial \mathcal{L}(a^{[2]}, y)}{\partial a^{[2]}} \cdot \frac{\partial a^{[2]}}{\partial z^{[2]}} = a^{[2]} - y
\]
\[dw^{[2]} = \frac{\partial \mathcal{L}(a^{[2]}, y)}{\partial a^{[2]}} \cdot \frac{\partial a^{[2]}}{\partial z^{[2]}}\cdot \frac{\partial z^{[2]}}{\partial w^{[2]}} = dz^{[2]}\cdot a^{[1]T}
\]
\[db^{[2]} = \frac{\partial \mathcal{L}(a^{[2]}, y)}{\partial a^{[2]}} \cdot \frac{\partial a^{[2]}}{\partial z^{[2]}}\cdot \frac{\partial z^{[2]}}{\partial b^{[2]}} = dz^{[2]}
\]
\[da^{[1]} = \frac{\partial \mathcal{L}(a^{[2]}, y)}{\partial a^{[2]}} \cdot \frac{\partial a^{[2]}}{\partial z^{[2]}} \cdot \frac{\partial z^{[2]}}{\partial a^{[1]}} = dz^{[2]} \cdot w^{[2]}
\]
\[dz^{[1]} = \frac{\partial \mathcal{L}(a^{[2]}, y)}{\partial a^{[2]}} \cdot \frac{\partial a^{[2]}}{\partial z^{[2]}} \cdot \frac{\partial z^{[2]}}{\partial a^{[1]}} \cdot \frac{\partial a^{[1]}}{\partial z^{[1]}}= dz^{[2]} \cdot w^{[2]} × g^{[1]’}(z^{[1]})
\]
\[dw^{[1]} = \frac{\partial \mathcal{L}(a^{[2]}, y)}{\partial a^{[2]}} \cdot \frac{\partial a^{[2]}}{\partial z^{[2]}} \cdot \frac{\partial z^{[2]}}{\partial a^{[1]}} \cdot \frac{\partial a^{[1]}}{\partial z^{[1]}} \cdot \frac{\partial z^{[1]}}{\partial w^{[1]}}= dz^{[1]} \cdot X^T
\]
\[db^{[1]} = \frac{\partial \mathcal{L}(a^{[2]}, y)}{\partial a^{[2]}} \cdot \frac{\partial a^{[2]}}{\partial z^{[2]}} \cdot \frac{\partial z^{[2]}}{\partial a^{[1]}} \cdot \frac{\partial a^{[1]}}{\partial z^{[1]}} \cdot \frac{\partial z^{[1]}}{\partial b^{[1]}}= dz^{[1]}
\]
这便是反向传播的整个推导过程，在具体的算法实现过程中，使用梯度下降的方法，不断进行更新。
