神经网络

什么是神经网络

机器学习领域所说的神经网络，指的是一种模仿生物神经网络的结构和功能而建立的数学或计算模型，用于对函数进行估计或近似。

层

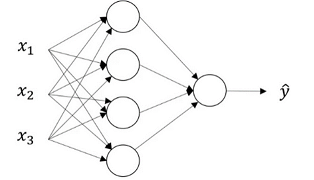
如图所示的神经网络中，前面为输入层，中间为隐藏层 ，最后为输出层。
中间层被称为隐藏层的原因是因为在训练过程中，将看到输入的样本有哪些，输出的结果是什么，中间层中的神经节点产生的真实值无法被观察到。所以中间层被称为隐藏层，只是因为你不会在训练集中看到它。
图中的这个神经网络也被称为两层神经网络，输入层不参与计算，所以计算神经网络的层数时，通常不考虑输入层。所以这个神经网络中，隐藏层是第一层，输出层是第二层，而输入层为第零层。

符号约定

输入特征：\(a^{[0]}\),上标“[ ]”括号中的数字表示神经网络中的第几层，a代表着激活（Activation），指的是不同层次的神经网络传递给后续层次的值。
将输入集传递给隐藏层后，隐藏层随之产生激活表示为\(a^{[1]}\)，而隐藏层的第一节点生成的激活表示为\(a^{[1]}_1\),第二个节点产生的激活为\(a^{[1]}_2\)以此类推，则：

\[{ a^{[1]} = \begin{bmatrix} a^{[1]}_1 \\ a^{[1]}_2 \\ a^{[1]}_3 \\ a^{[1]}_4 \end{bmatrix}\quad} \]

最后，输出层输出的值表示为\(a^{[2]}\)，则\(\hat{y} = a^{[2]}\)。
图中的隐藏层中，将存在参数w和b，它们将分别表示为\(w^{[1]}\)和\(b^{[1]}\)将会是个4×3矩阵，\(w^{[1]}\)将会是个4×1矩阵。输出层中，也会存在参数\(w^{[2]}\)和\(b^{[2]}\)，\(w^{[2]}\)是个1×4矩阵，\(b^{[2]}\)是个1×1矩阵。

计算神经网络的输出

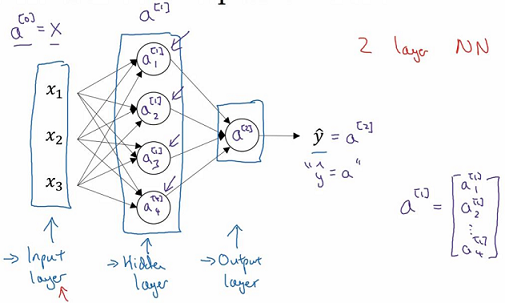
上面的计算过程可以表示为：
\(z_{1}^{[1]}=w_{1}^{[1] T} X+b_{1}^{[1]}, a_{1}^{[1]}=\sigma\left(z_{1}^{[1]}\right)\)
\(z_{2}^{[1]}=w_{2}^{[1] T} X+b_{2}^{[1]}, a_{2}^{[1]}=\sigma\left(z_{2}^{[1]}\right)\)
\(z_{3}^{[1]}=w_{3}^{[1] T} X+b_{3}^{[1]}, a_{3}^{[1]}=\sigma\left(z_{4}^{[1]}\right)\)
\(z_{4}^{[1]}=w_{4}^{[1] T} X+b_{4}^{[1]}, a_{4}^{[1]}=\sigma\left(z_{4}^{[1]}\right)\)

将它们都表示成矩阵形式：

\[z^{[1]}=\left[ \begin{array}{ccc}{w_{1}^{[1]}} & {w_{1}^{[1]}} & {w_{1}^{[1]}} \\ {w_{2}^{[1]}} & {w_{2}^{[1]}} & {w_{2}^{[1]}} \\ {w_{3}^{[1]}} & {w_{3}^{[1]}} & {w_{3}^{[1]}} \\ {w_{4}^{[1]}} & {w_{4}^{[1]}} & {w_{4}^{[1]}}\end{array}\right] \quad \left[ \begin{array}{c}{x_{1}} \\ {x_{2}} \\ {x_{3}}\end{array}\right]+\left[ \begin{array}{c}{b_{1}^{[1]}} \\ {b_{2}^{[1]}} \\ {b_{3}^{[1]}} \\ {b_{4}^{[1]}}\end{array}\right]=\left[ \begin{array}{c}{z_{1}^{[1]}} \\ {z_{2}^{[1]}} \\ {z_{3}^{[1]}} \\ {z_{4}^{[1]}}\end{array}\right] \]

即：
\(z^{[1]}=w^{[1]} X+b^{[1]}\)
\(a^{[1]}=\sigma\left(z^{[1]}\right)\)
\(z^{[2]}=w^{[2]} a^{[1]}+b^{[2]}\)
\(a^{[2]}=\sigma\left(z^{[2]}\right)\)

参数矩阵\({w^{[l]}}\)的大小是：\({n^{[l]}}*{n^{[l - 1]}}\)。
参数\(b^{[l]}\)的大小为：\(b^{[l]}*1\)。
逻辑回归中，直接将两个参数都初始化为零。而在神经网络中，通常将参数w进行随机初始化，参数b则初始化为0。
除w、b外的各种参数，如学习率α、神经网络的层数l，第l层包含的节点数\(n^{[l]}\)及隐藏层中用的哪种激活函数，都称为超参数（Hyper Parameters），因为它们的值决定了参数w、b最后的值。