python 实现
库和数据导入
导入库
HDF(Hierarchical Data Format)指一种为存储和处理大容量科学数据设计的文件格式及相应库文件。python 中有一系列的工具可以操作和使用 HDF5 数据,其中最常用的是 h5py 和 PyTables。
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
导入数据
def load_dataset():
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
查看图片
可以调用以下方法来查看训练集或测试集中的图片:
## 显示图片
def image_show(index,dataset):
index = index
if dataset == "train":
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]) + ", 它是一张" + classes[np.squeeze(train_set_y[:, index])].decode("utf-8") + "' 图片。")
elif dataset == "test":
plt.imshow(test_set_x_orig[index])
print ("y = " + str(test_set_y[:, index]) + ", 它是一张" + classes[np.squeeze(test_set_y[:, index])].decode("utf-8") + "' 图片。")
基本函数模块
sigmoid函数
def sigmoid(z):
s = 1/(1+np.exp(-z))
return s
初始化参数w,b
def initialize_with_zeros(dim):
w = np.zeros((dim,1)) #w为一个dim*1矩阵
b = 0
return w, b
计算Y_hat,成本函数J以及dw,db
def propagate(w, b, X, Y):
m = X.shape[1] #样本个数
Y_hat = sigmoid(np.dot(w.T,X)+b)
cost = -(np.sum(np.dot(Y,np.log(Y_hat).T)+np.dot((1-Y),np.log(1-Y_hat).T)))/m #成本函数
dw = (np.dot(X,(Y_hat-Y).T))/m
db = (np.sum(Y_hat-Y))/m
cost = np.squeeze(cost) #压缩维度
grads = {"dw": dw,
"db": db} #梯度
return grads, cost
梯度下降找出最优解
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):#num_iterations-梯度下降次数 learning_rate-学习率,即参数ɑ
costs = [] #记录成本值
for i in range(num_iterations): #循环进行梯度下降
grads, cost = propagate(w,b,X,Y)
dw = grads["dw"]
db = grads["db"]
w = w - learning_rate*dw
b = b - learning_rate*db
if i % 100 == 0: #每100次记录一次成本值
costs.append(cost)
if print_cost and i % 100 == 0: #打印成本值
print ("循环%i次后的成本值: %f" %(i, cost))
params = {"w": w,
"b": b} #最终参数值
grads = {"dw": dw,
"db": db}#最终梯度值
return params, grads, costs
得出预测结果
def predict(w, b, X):
m = X.shape[1] #样本个数
Y_prediction = np.zeros((1,m)) #初始化预测输出
w = w.reshape(X.shape[0], 1) #转置参数向量w
Y_hat = sigmoid(np.dot(w.T,X)+b) #最终得到的参数代入方程
for i in range(Y_hat.shape[1]):
if Y_hat[:,i]>0.5:
Y_prediction[:,i] = 1
else:
Y_prediction[:,i] = 0
return Y_prediction
模型创建
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.5, print_cost = False): #num_iterations-梯度下降次数 learning_rate-学习率,即参数ɑ
w, b = initialize_with_zeros(X_train.shape[0]) #初始化参数w,b
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost) #梯度下降找到最优参数
w = parameters["w"]
b = parameters["b"]
Y_prediction_train = predict(w, b, X_train) #训练集的预测结果
Y_prediction_test = predict(w, b, X_test) #测试集的预测结果
train_accuracy = 100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100 #训练集识别准确度
test_accuracy = 100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100 #测试集识别准确度
print("训练集识别准确度: {} %".format(train_accuracy))
print("测试集识别准确度: {} %".format(test_accuracy))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
模型执行与测试
初始化样本,输入模型,得出结果
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
m_train = train_set_x_orig.shape[0] #训练集中样本个数
m_test = test_set_x_orig.shape[0] #测试集总样本个数
num_px = test_set_x_orig.shape[1] #图片的像素大小
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T #原始训练集的设为(12288*209)
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T #原始测试集设为(12288*50)
train_set_x = train_set_x_flatten/255. #将训练集矩阵标准化
test_set_x = test_set_x_flatten/255. #将测试集矩阵标准化
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
输出结果:
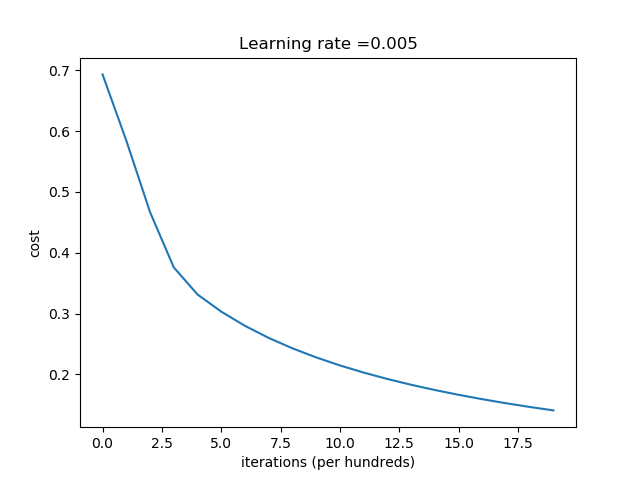
循环0次后的成本值: 0.693147
循环100次后的成本值: 0.584508
循环200次后的成本值: 0.466949
循环300次后的成本值: 0.376007
循环400次后的成本值: 0.331463
循环500次后的成本值: 0.303273
循环600次后的成本值: 0.279880
循环700次后的成本值: 0.260042
循环800次后的成本值: 0.242941
循环900次后的成本值: 0.228004
循环1000次后的成本值: 0.214820
循环1100次后的成本值: 0.203078
循环1200次后的成本值: 0.192544
循环1300次后的成本值: 0.183033
循环1400次后的成本值: 0.174399
循环1500次后的成本值: 0.166521
循环1600次后的成本值: 0.159305
循环1700次后的成本值: 0.152667
循环1800次后的成本值: 0.146542
循环1900次后的成本值: 0.140872
训练集识别准确度: 99.04306220095694 %
测试集识别准确度: 70.0 %
绘制学习曲线
costs = np.squeeze(d['costs'])
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(d["learning_rate"]))
plt.show()
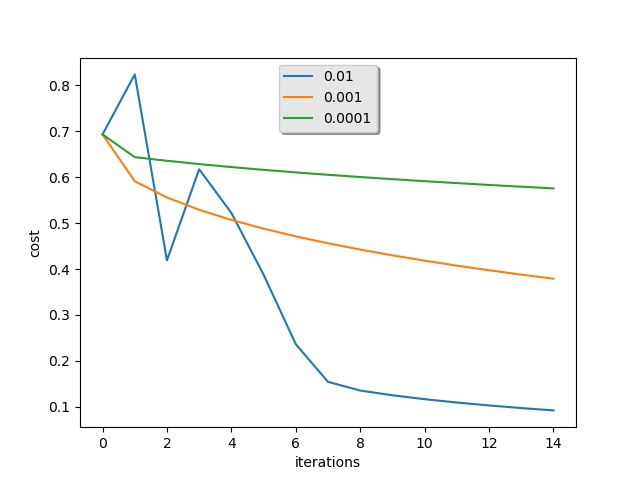
不同的学习率的影响
learning_rates = [0.01, 0.001, 0.0001]
models = {}
for i in learning_rates:
print ("学习率: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
输出结果:
学习率: 0.01
训练集识别准确度: 99.52153110047847 %
测试集识别准确度: 68.0 %
-------------------------------------------------------
学习率: 0.001
训练集识别准确度: 88.99521531100478 %
测试集识别准确度: 64.0 %
-------------------------------------------------------
学习率: 0.0001
训练集识别准确度: 68.42105263157895 %
测试集识别准确度: 36.0 %


 浙公网安备 33010602011771号
浙公网安备 33010602011771号