Logistic回归模型

Logistic回归是一种用于解决监督学习（Supervised Learning）问题的学习算法。
进行Logistic回归的目的，是使训练数据的标签值与预测出来的值之间的误差最小化。
猫图分类器中，要实现的是：对于给定的以 \(n_x\) 维特征向量 \(x\) 表示、标签为 \(y\) 的一张图片，估计出这张图片为猫图的概率 \(\hat{y}\) ，即：

\[\hat{y} = p(y = 1|x), 0 \le \hat{y} \le 1 \]

有大量猫图的数据时，考虑采用线性拟合的方法，来找到一个 \(\hat{y}\) 关于 \(x\) 的函数，从而实现这个猫分类器。规定一个 \(n_x\) 维向量 \(w\) 和一个值 \(b\) 作为参数，可得到线性回归的表达式：

\[{\hat{y} = w^Tx + b} \]

由于 \(\hat{y}\) 为概率值，取值范围为[0,1]，简单地进行线性拟合，得出的 \(\hat{y}\) 可能非常大，还可能为负值。此时，就需要用一个Logistic回归单元来对其值域进行约束。这里以sigmoid函数为逻辑回归单元，其表达式为：

\[\sigma{(z)} = \frac{1}{1+e^{-z}} \]

函数图像为：

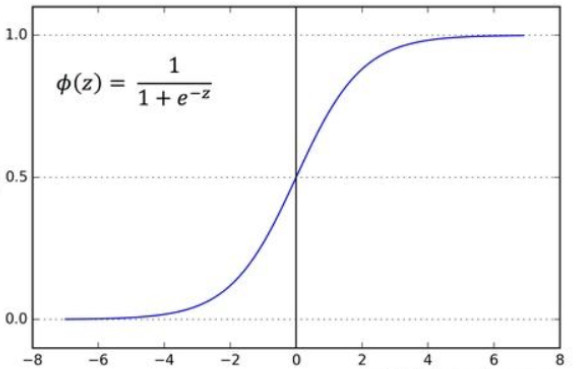
• 当z趋近于正无穷大时，σ(z)=1;
• 当z趋近于负无穷大时，σ(z)=0;
• 当z=0时，σ(z)=0.5。

所以可以用sigmoid函数来约束 \(\hat{y}\) 的值域，得到该分类器的Logistic回归模型：

\[{ \hat{y} = σ(w^Tx + b) = \frac{1}{1+e^{-(w^Tx + b)}}} \]

建立好Logistic回归模型后，接下来要考虑的是如何利用我们的训练集数据，找到该模型中的两个参数 \(w\) 和 \(b\) 的最优解。