二分类

Logistic回归常用于解决二分类（Binary Classification）问题。在二分类问题中，对于某个输入，输出的结果是离散的值。
例如：想要构建一个猫图分类器，即输入一张图片，希望该分类器准确判断出该图片是否是一张猫图，并输出它的预测结果。

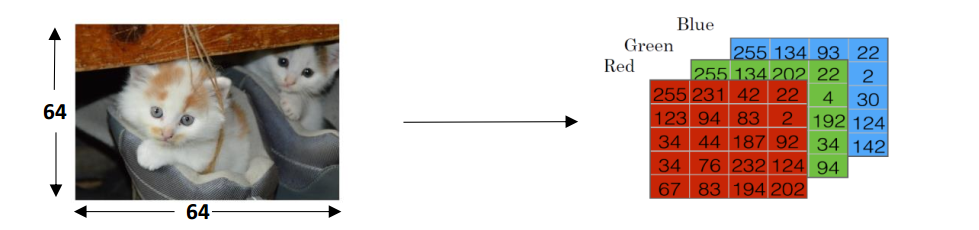
图片是一类非结构化的数据，一张图片在计算机中以RGB编码时，是以红、绿、蓝为三基色，每个像素点上三基色对应的量的多少（即“亮度”）编码为数据进行存储。
在模式识别（Pattern Recognition）以及机器学习中，对于处理的各种类型的数据，通常采用一些特征向量来表示。简单地将一张猫图表示为一个特征向量，可以直接把三个矩阵进行拆分重塑，最终形成维数\(n_x = 64 \times 64 \times 3 = 12288\):

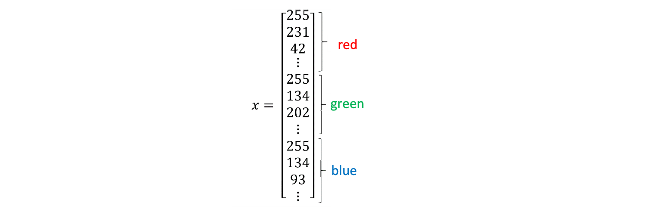
实现这个分类器，需要准备大量的猫图及少量的非猫图，并取其中大部分组成该分类器的训练样本，少部分组成测试样本。
将这些样本都以上述的方式表示为特征向量的形式，一个样本由一对 \((x,y)\) 进行表示，其中 \(x\) 为 \(n_x\) 维的特征向量， \(y\) 是该特征向量的标签（Label），根据该特征向量表示的是猫或非猫，取值为0或1。如果有m个训练样本对，它们将被表示为：

\[{(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),…,(x^{(m)},y^{(m)})} \]

更进一步，可以用矩阵的形式将我们的数据表示得更为紧凑。训练集中所有特征向量以及它们的标签分别进行列组合，变成两个矩阵：

\[{X = [x^{(1)},x^{(2)},…,x^{(m)}]} \]

\[{Y = [y^{(1)},y^{(2)},…,y^{(m)}]} \]

这样， \(X\) 会是个大小为 \(n_x \times m\) 的矩阵，\(Y\)是个大小为 \(1×m\) 的矩阵。