66 构建乘积数组

题目

给定一个数组 A[0,1,...,n−1A[0,1,...,n−1]，请构建一个数组 B[0,1,...,n−1]B[0,1,...,n−1]。 其中 B 中的元素 B[i]=A[0] x A[1] x ... x A[i−1] x A[i+1]  x ... x A[n−1]。不能使用除法。

C++ 题解

如果没有不能使用除法的限制,可以用公式B[i]=A[0] x A[1] x ..... x A[n-1]/A[i]表示,使用除法时要特别注意A[i]等于0的情况。
现好在还有更高效的算法。可以把B[i]=A[0] x A[1] x ..... x A[i-1] x A[i+1] x ..... x A[n-1]。看成A[0] x A[1] x ..... x A[i-1]和A[i+1] x .....A[n-2] x A[n-1]两部分的乘积。
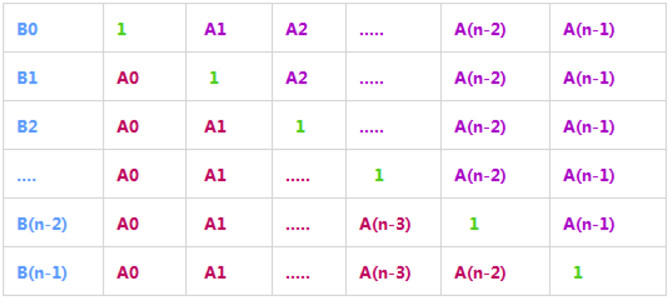
因此，数组B可以用一个矩阵来创建。在图中，B[i]为矩阵中第i行所有元素的乘积：

牛客网 OJ
AcWing OJ

public class Solution {
    public int[] multiply(int[] A) {
        int length = A.length;
        int[] B = new int[length];
        if(length != 0 ){
            B[0] = 1;
            //计算下三角连乘
            for(int i = 1; i < length; i++){
                B[i] = B[i-1] * A[i-1];
            }
            int temp = 1;
            //计算上三角
            for(int j = length-2; j >= 0; j--){
                temp *= A[j+1];
                B[j] *= temp;
            }
        }
        return B;
    }
}

python 题解

方法一

基本解法：

# -*- coding:utf-8 -*-
class Solution:
    def multiply(self, A):
        # write code here
        n=len(A)
        C=[1]*len(A)
        D=[1]*len(A)
        B=[1]*len(A)
        for i in range(1,n):
            C[i]=C[i-1]*A[i-1]
        for j in (range(0,n-1))[::-1]:
            D[j]=D[j+1]*A[j+1]
        
        for k in range(0,n):
            B[k]=C[k]*D[k]
        return B

方法二

# -*- coding:utf-8 -*-
class Solution:
    def multiply(self, A):
        # write code here
        B=[1]*len(A)
        for i in range(1,len(A)):
            B[i]=B[i-1]*A[i-1]
            
        tmp=1
        for j in range(len(A)-2,-1,-1):
            tmp *= A[j+1]
            B[j]*= tmp
        return B