51 数组中的逆序对

题目

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数：如数组{7,5,6,4}，逆序对总共有5对，{7,5}，{7,6}，{7,4}，{5,4}，{6,4}；

牛客网 OJ
AcWing OJ

思路

基于归并排序的思想统计逆序对：
先把数组分割成子数组，在子数组合并的过程中统计逆序对的数目。
统计逆序对时，先统计子数组内部的逆序对的数目，再统计相邻子数组的逆序对数目。
基于归并思想统计逆序对的过程

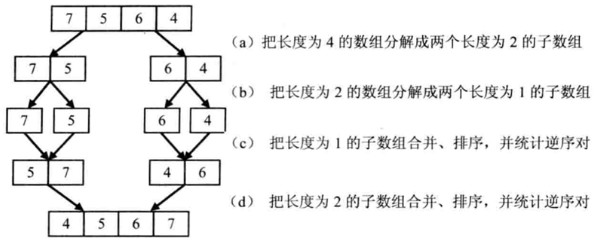
合并子数组统计逆序对的过程
把长度为2的子数组合并、排序并统计逆序对的过程。

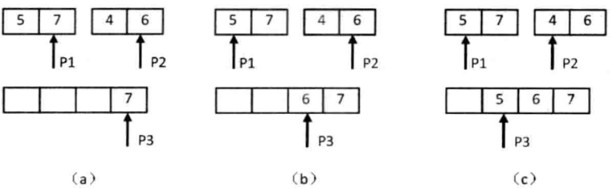
C 语言题解

int InversePairsCore(int* data, int* copy, int start, int end);

int InversePairs(int* data, int length)
{
    if(data == nullptr || length < 0)
        return 0;

    int* copy = new int[length];
    for(int i = 0; i < length; ++i)
        copy[i] = data[i];

    int count = InversePairsCore(data, copy, 0, length - 1);
    delete[] copy;

    return count;
}

int InversePairsCore(int* data, int* copy, int start, int end)
{
    if(start == end)
    {
        copy[start] = data[start];
        return 0;
    }

    int length = (end - start) / 2;

    int left = InversePairsCore(copy, data, start, start + length);
    int right = InversePairsCore(copy, data, start + length + 1, end);

    // i初始化为前半段最后一个数字的下标
    int i = start + length;
    // j初始化为后半段最后一个数字的下标
    int j = end;
    int indexCopy = end;
    int count = 0;
    while(i >= start && j >= start + length + 1)
    {
        if(data[i] > data[j])
        {
            copy[indexCopy--] = data[i--];
            count += j - start - length;
        }
        else
        {
            copy[indexCopy--] = data[j--];
        }
    }

    for(; i >= start; --i)
        copy[indexCopy--] = data[i];

    for(; j >= start + length + 1; --j)
        copy[indexCopy--] = data[j];

    return left + right + count;
}

C++ 题解

class Solution {
public:
    int InversePairs(vector<int> data) {
        if(data.size()==0)
            return 0;
        vector<int> copy(data);    // 辅助数组，每次递归后有序
        return InversePairsCore(data, copy, 0, data.size()-1);
    }

    int InversePairsCore(vector<int>& data, vector<int>& copy, int begin, int end) 
    {
        if(begin == end)
            return 0;
        
        int mid = begin + (end-begin)/2;
        int left = InversePairsCore(copy, data, begin, mid);
        int right = InversePairsCore(copy, data, mid+1, end);
        
        int last_in_left = mid;		// 比较从尾端开始
        int last_in_right = end;	// 比较从尾端开始
        int index_copy = end; 		// 比较结果存入辅助数组尾端
        long res = 0;
        
        // 归并排序：相当于两个有序数组合成一个有序表（从尾端开始是为了计数）
        while(last_in_left>=begin && last_in_right>=mid+1)
        {
            if(data[last_in_left] > data[last_in_right]) 
            {
                copy[index_copy--] = data[last_in_left--];
                res += last_in_right - mid;
            }
            else 
                copy[index_copy--] = data[last_in_right--];
        }
        
        while(last_in_left >= begin)
            copy[index_copy--] = data[last_in_left--];
        while(last_in_right >= mid+1)
            copy[index_copy--] = data[last_in_right--];
        
        return (left+right+res);
    }
};

python 题解

# -*- coding:utf-8 -*-
class Solution:    
    #归并排序法
    def InversePairs(self, data):
        if len(data)<=0:
            return 0
        length=len(data)
        copy=[0]*length
        for i in range(length):
            copy[i]=data[i]
        #copy数组为原数组data的复制,在后面充当辅助数组
        count=self.Core(data,copy,0,length-1)
        return count % 1000000007
    
    def Core(self,data,copy,start,end):
        if start==end:
            copy[start]=data[start]
            return 0

        length=(end-start)//2 #length为划分后子数组的长度

        left=self.Core(copy,data,start,start+length)
        right=self.Core(copy,data,start+length+1,end)

        #初始化i为前半段最后一个数字的下标
        i=start+length
        #初始化j为后半段最后一个数字的下标
        j=end

        #indexCopy为辅助数组的指针，初始化其指向最后一位
        indexCopy=end
        #准备开始计数
        count=0
        #对两个数组进行对比取值的操作：
        while i>=start and j>=start+length+1:
            if data[i]>data[j]:
                copy[indexCopy]=data[i]
                indexCopy-=1
                i-=1
                count += j-start-length
            else:
                copy[indexCopy]=data[j]
                indexCopy-=1
                j-=1
        
        #剩下一个数组未取完的操作：
        while i>=start:
            copy[indexCopy]=data[i]
            indexCopy-=1
            i-=1
        while j>=start+length+1:
            copy[indexCopy]=data[j]
            indexCopy-=1
            j-=1
        
        return count+left+right