23 链表中环的入口结点
题目
如果一个链表中包含环,如何找到环的入口节点?
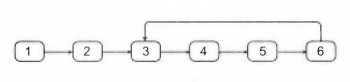
例如:1–>2–>3–>4–>5–>6(–>3),在6后并没有结束,其next指向了中间的3,形成了一个环,所以环的入口节点是节点3。
C++ 题解
- 第一步确定链表中是否包含环,我们定义两个指针:快慢指针,慢指针每次走一步,快指针每次走两步,如果它俩重合了,这就说明链表中存在环。
- 第二步求环的长度,两者碰头后,让其中一个继续走,每走一步步数加一,然后求得环的长度。
- 第三步求环的初始节点,仍然是两个指针,其中一个事先走环长个节点,假设环长为n,然后另一个指针从头开始移动,两者之间的间距为n一直保持,那么当两者碰头时,相遇额节点就是环的入口节点,此时第一个指针比第二个指针正好多走了环长(n)个节点。
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* pHead)
{
ListNode* meet = MeetingNode(pHead);
if(!meet)
return nullptr;
ListNode* p1 = meet->next;
unsigned int NodeNum = 1;
while(p1 != meet)
{
p1 = p1->next;
NodeNum++;
}
p1 = pHead;
ListNode* p2 = pHead;
for (int i=0;i<NodeNum;i++)
p1 = p1->next;
while(p1!=p2)
{
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
// 判断链表中是否有环
ListNode* MeetingNode(ListNode* pHead)
{
if (pHead == nullptr)
return nullptr;
ListNode* pSlow = pHead->next;
if (pSlow == nullptr)
return nullptr;
ListNode* pFast = pSlow->next;
// 慢指针每次前进一步
// 快指针每次前进两步
// 在前进过程中不可能碰到nullptr,一旦碰到,跳出循环,并且链表中无环
while (pFast != nullptr && pSlow != nullptr)
{
// 两个指针相遇,说明链表有环,返回相遇节点
if (pFast == pSlow)
return pFast;
pSlow = pSlow->next;
pFast = pFast->next;
if (pFast != nullptr)
pFast = pFast->next;
}
return nullptr;
}
};
python 题解
方法一
思路与C++题解一致
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def EntryNodeOfLoop(self, pHead):
# write code here
pMeet = self.Meeting(pHead)
if not pMeet:
return None
p1 = pMeet.next
nodeNum = 1;
while p1 != pMeet:
p1 = p1.next
nodeNum += 1
p1 = pHead
p2 = pHead
for i in range(nodeNum):
p1 = p1.next
while p1 != p2:
p1 = p1.next
p2 = p2.next
return p1
def Meeting(self,pHead):
if not pHead:
return None
pSlow = pHead
pFast = None
if pSlow.next:
pFast = pSlow.next
while pSlow and pFast:
if pFast == pSlow:
return pFast
pSlow = pSlow.next
pFast = pFast.next
if pFast.next:
pFast = pFast.next
return None
方法二
- 两个指针一个fast、一个slow同时从一个链表的头部出发,fast一次走2步,slow一次走一步,如果该链表有环,两个指针必然在环内相遇。
- 此时只需要把其中的一个指针重新指向链表头部,另一个不变(还在环内),这次两个指针一次走一步,相遇的地方就是入口节点。
上述关系的证明:
- 链表头到环入口长度为--a
- 环入口到相遇点长度为--b
- 相遇点到环入口长度为--c
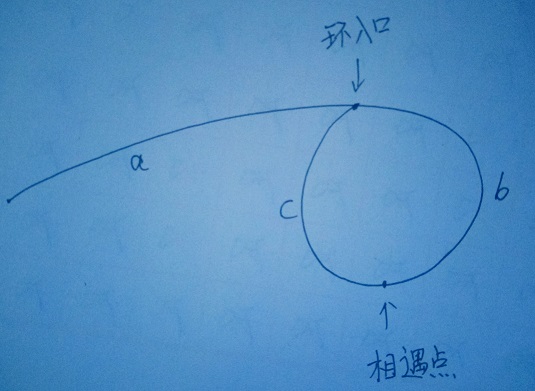
则:相遇时:
快指针路程=a+(b+c)k+b ,k>=1 其中b+c为环的长度,k为绕环的圈数(k>=1,即最少一圈,不能是0圈,不然和慢指针走的一样长,矛盾)。
慢指针路程=a+b
快指针走的路程是慢指针的两倍,所以:(a+b)x 2 = a+(b+c)k+b
化简可得:**a=(k-1)(b+c)+c **
这个式子的意思是: 链表头到环入口的距离=相遇点到环入口的距离+(k-1)圈环长度。其中k>=1,所以k-1>=0圈。所以两个指针分别从链表头和相遇点出发,最后一定相遇于环入口。
# -*- coding:utf-8 -*-
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def EntryNodeOfLoop(self, pHead):
# write code here
if not pHead:
return None
pFast = pHead
pSlow = pHead
while pFast and pFast.next:
pFast = pFast.next.next
pSlow = pSlow.next
if pFast == pSlow:
break
if pFast == None or pFast.next == None:
return None
pFast = pHead
while pFast != pSlow:
pFast = pFast.next
pSlow = pSlow.next
return pSlow
注意:
- 此时不需要统计环中节点的数目。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号