10 斐波那契数列
题目
写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。斐波那契数列的定义如下:
C++ 题解
方法一
递归解法,不推荐,效率低:
long long Fibonacci_Solution1(unsigned int n)
{
if(n <= 0)
return 0;
if(n == 1)
return 1;
return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2);
}
方法二
循环解法:
long long Fibonacci_Solution2(unsigned int n)
{
int result[2] = { 0, 1 };
if (n < 2)
return result[n];
long long fibNMinusOne = 1;
long long fibNMinusTwo = 0;
long long fibN = 0;
for (unsigned int i = 2; i <= n; ++i)
{
fibN = fibNMinusOne + fibNMinusTwo;
fibNMinusTwo = fibNMinusOne;
fibNMinusOne = fibN;
}
return fibN;
}
python 题解
方法一
递归:
# -*- coding:utf-8 -*-
class Solution:
def Fibonacci(self, n):
# write code here
if n<=0:
return 0
elif n==1:
return 1
return self.Fibonacci(n-1)+self.Fibonacci(n-2)
方法二
循环方法:
class Solution(object):
def Fibonacci(self, n):
"""
:type n: int
:rtype: int
"""
if n <= 0:
return 0
if n == 1:
return 1
fibone = 1
fibtwo = 0
fibN = 0
for i in range(2,n+1):
fibN = fibone + fibtwo
fibtwo,fibone = fibone,fibN
return fibN
青蛙跳台阶
扩展1
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
# -*- coding:utf-8 -*-
class Solution:
def jumpFloor(self, number):
# write code here
if number==1:
return 1
if number==2:
return 2
small,big=1,2
for i in range(2,number):
sum_i=small+big
small=big
big=sum_i
return big
扩展2
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
# -*- coding:utf-8 -*-
class Solution:
def jumpFloorII(self, number):
# write code here
if number<=0:
return 0
return 2**(number-1)
矩形覆盖
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
这道题本质上还是斐波那契数列问题,注意分析n=0,1,2,3,...的值的情况。
# -*- coding:utf-8 -*-
class Solution:
def rectCover(self, number):
# write code here
if number<=0:
return 0
if number==1:
return 1
if number==2:
return 2
small,big=1,2
for i in range(3,number+1):
sum_i=small+big
small=big
big=sum_i
return big

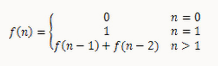

 浙公网安备 33010602011771号
浙公网安备 33010602011771号