11 旋转数组的最小数字
题目
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
C 语言题解
从头到尾遍历数组一次,我们就能找出最小的元素。这种思路的时间复杂度显然是O(n)。但是这个思路没有利用输入的旋转数组的特性,肯定达不到面试官的要求。
我们还注意到最小的元素刚好是这两个子数组的分界线,在排序的数组中我们可以用二分查找法实现O(logn)的查找。
- 和二分查找法一样,我们用两个指针分别指向数组的第一个元素和最后一个元素。
- 接着我们可以找到数组中间的元素:
如果该中间元素位于前面的递增子数组,那么它应该大于或者等于第一个指针指向的元素。此时数组中最小的元素应该位于该中间元素的后面。我们可以把第一个指针指向该中间元素,这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组之中。如果中间元素位于后面的递增子数组,那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小的元素应该位于该中间元素的前面。 - 接下来我们再用更新之后的两个指针,重复做新一轮的查找。
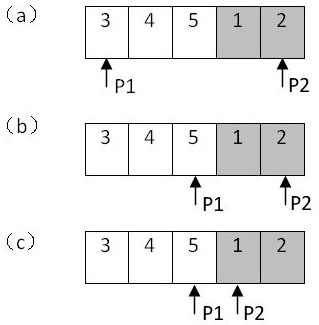
以前面的数组{3,4,5,1,2}为例,下图展示了在该数组中查找最小值的过程:
int MinInOrder(int* numbers, int index1, int index2);
int Min(int *numbers, int length)
{
if (numbers == nullptr || length <= 0)
throw new std::exception("Invalid parameters");
int index1 = 0;
int index2 = length - 1;
int indexMid = index1;
while (numbers[index1] >= numbers[index2])
{
// 如果index1和index2指向相邻的两个数,
// 则index1指向第一个递增子数组的最后一个数字,
// index2指向第二个子数组的第一个数字,也就是数组中的最小数字
if (index2 - index1 == 1)
{
indexMid = index2;
break;
}
// 如果下标为index1、index2和indexMid指向的三个数字相等,
// 则只能顺序查找
indexMid = (index1 + index2) / 2;
if (numbers[index1] == numbers[index2] && numbers[indexMid] == numbers[index1])
return MinInOrder(numbers, index1, index2);
// 缩小查找范围
if (numbers[indexMid] >= numbers[index1])
index1 = indexMid;
else if (numbers[indexMid] <= numbers[index2])
index2 = indexMid;
}
return numbers[indexMid];
}
int MinInOrder(int* numbers, int index1, int index2)
{
int result = numbers[index1];
for (int i = index1 + 1; i <= index2; ++i)
{
if (result > numbers[i])
result = numbers[i];
}
return result;
}
C++ 题解
class Solution {
public:
int minNumberInRotateArray(vector<int> rotateArray) {
int size = rotateArray.size();
if(size == 0){
return 0;
}
int left = 0,right = size - 1;
int mid = 0;
while(rotateArray[left] >= rotateArray[right]){
if(right - left == 1){
mid = right;
break;
}
// 移位运算优先级低于算术运算,需要加上括号
mid = left + ((right - left) >> 1);
if(rotateArray[left] == rotateArray[right] && rotateArray[left] == rotateArray[mid]){
return MinOrder(rotateArray,left,right);
}
if(rotateArray[mid] >= rotateArray[left]){
left = mid;
}
else{
right = mid;
}
}
return rotateArray[mid];
}
// 顺序寻找最小值
int MinOrder(vector<int> &num,int left,int right){
int result = num[left];
for(int i = left + 1;i < right;++i){
if(num[i] < result){
result = num[i];
}
}
return result;
}
};
python 题解
# -*- coding:utf-8 -*-
class Solution:
def minNumberInRotateArray(self, rotateArray):
# write code here
length = len(rotateArray)
if length == 0:
return 0
left = 0
right = length - 1
mid = 0
while rotateArray[left] >= rotateArray[right]:
if right - left == 1:
mid = right
break
# 中间位置查找的两种方法:
#mid = (right+left)//2
mid = left + ((right-left)//2)
if rotateArray[left] == rotateArray[right] and rotateArray[left] == rotateArray[mid]:
return self.MinRoder(rotateArray,left,right)
# 注意等号不可以缺省
if rotateArray[mid] >= rotateArray[left]:
left = mid
else:
right = mid
return rotateArray[mid]
def MinRoder(self,array,left,right):
res = array[left]
for i in array[left+1:right+1]:
if i < res:
res = i
return res


 浙公网安备 33010602011771号
浙公网安备 33010602011771号