07 重建二叉树

题目

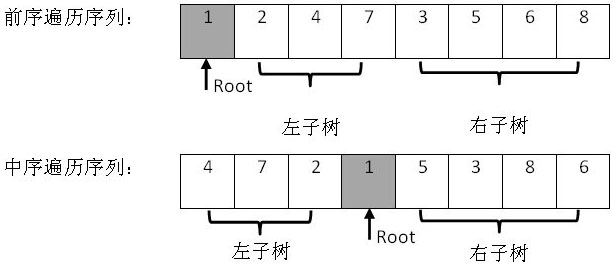
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示的二叉树并输出它的头结点。　

牛客网 OJ
AcWing OJ

C++ 题解

先根据前序遍历序列的第一个数字创建根结点，接下来在中序遍历序列中找到根结点的位置，这样就能确定左、右子树结点的数量。在前序遍历和中序遍历的序列中划分了左、右子树结点的值之后，就可以递归地去分别构建它的左右子树。

/**
 * Definition for binary tree
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) 
    {
        int inlen = vin.size();
        if (inlen == 0)
            return nullptr;
        
        vector<int> left_pre,right_pre,left_in,right_in;
        
        // 创建根节点，根节点是前序遍历序列中的第一个节点
        TreeNode* head = new TreeNode(pre[0]);
        
        // 在中序遍历中找到根节点的位置
        int rootPos = 0;
        for(int i=0;i<inlen;i++)
        {
            if (vin[i] == pre[0])
            {
                rootPos = i;
                break;
            }           
        }
        
        // 在中序遍历中，位于根节点左侧的节点都是根节点的左子节点
        // 在前序遍历中，根节点的左子节点位于序列的前面，节点的个数一定是与在中序中划分的左子节点的个数一致
        for(int i=0;i<rootPos;i++)
        {
            left_in.push_back(vin[i]);
            left_pre.push_back(pre[i+1]);
        }
        
        // 在中序遍历中，位于根节点右侧的节点都是根节点的右子节点
        // 在前序遍历中，根节点的右子节点位于序列的后面，节点的个数一定是与在中序中划分的右子节点的个数一致
        for(int i=rootPos+1;i<inlen;i++)
        {
            right_in.push_back(vin[i]);
            right_pre.push_back(pre[i]);
        }    
        
        // 采用递归的方法，重建左子树和右子树，直到叶节点
        head->left=reConstructBinaryTree(left_pre,left_in);
        head->right=reConstructBinaryTree(right_pre,right_in);
        
        return head;      

    }
};

python 题解

# -*- coding:utf-8 -*-
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    # 返回构造的TreeNode根节点
    def reConstructBinaryTree(self, pre, tin):
        # write code here
        if not pre or not tin:
            return None
        
        root = TreeNode(pre[0])
        rootIndex = tin.index(pre[0]) 
        
        root.left = self.reConstructBinaryTree(pre[1:rootIndex+1],tin[:rootIndex])
        root.right = self.reConstructBinaryTree(pre[rootIndex+1:],tin[rootIndex+1:])
        
        return root        

注意：

• python 类中使用函数或者成员变量不要忘记添加self。