邻接矩阵和邻接表

示例图：

邻接矩阵

实现图的最简单的方法之一是使用二维矩阵。在该矩阵实现中，每个行和列表示图中的顶点。存储在行 v 和列 w 的交叉点处的单元中的值表示是否存在从顶点 v 到顶点 w 的边。
当两个顶点通过边连接时，我们说它们是相邻的。
单元格中的值表示从顶点 v 到顶点 w 的边的权重。

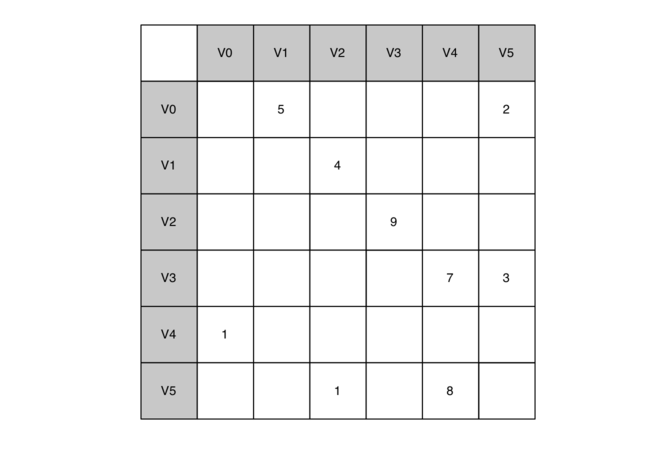
邻接矩阵的优点是简单，对于小图，很容易看到哪些节点连接到其他节点。 然而，注意矩阵中的大多数单元格是空的。 因为大多数单元格是空的，我们说这个矩阵是“稀疏的”。矩阵不是一种非常有效的方式来存储稀疏数据。
由于图中每个顶点有一行和一列，填充矩阵所需的边数为\({\left| V \right|^2}\)​​。 当每个顶点连接到每个其他顶点时，矩阵是满的。

邻接表

实现稀疏连接图的更空间高效的方法是使用邻接表。在邻接表实现中，我们保存Graph 对象中的所有顶点的主列表，然后图中的每个顶点对象维护连接到的其他顶点的列表。
在我们的顶点类的实现中，我们将使用字典而不是列表，其中字典键是顶点，值是权重。

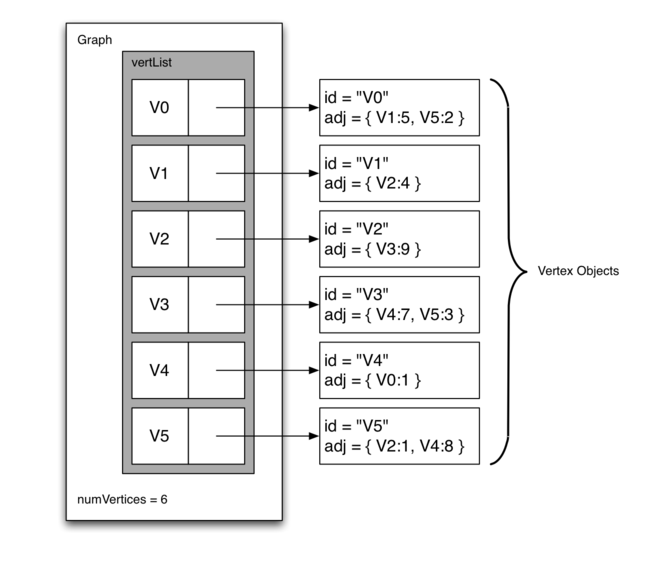
邻接表实现的优点是它允许我们紧凑地表示稀疏图。 邻接表还允许我们容易找到直接连接到特定顶点的所有链接。