图

图的基本概念

顶点

也称为“节点”，是图的基本部分。它可以有一个名称，我们将称为“键”。一个顶点也可能有额外的信息。我们将这个附加信息称为“有效载荷”。

边##

也称为“弧”，是图的另一个基本部分。边连接两个顶点，以表明它们之间存在关系。边可以是单向的或双向的。如果图中的边都是单向的，我们称该图是有向图。

权重##

可以被加权以示出从一个顶点到另一个顶点的成本。例如，在将一个城市连接到另一个城市的道路的图表中，边上的权重可以表示两个城市之间的距离。

图的描述

图可以由 G 表示，其中\({\rm{G = (V,E)}}\)对于图 G，V 是一组顶点，E 是一组边。每个边是一个元组\({\rm{(v,w)}}\)其中 \(w,v \in V\)。我们可以添加第三个组件到边元组来表示权重。
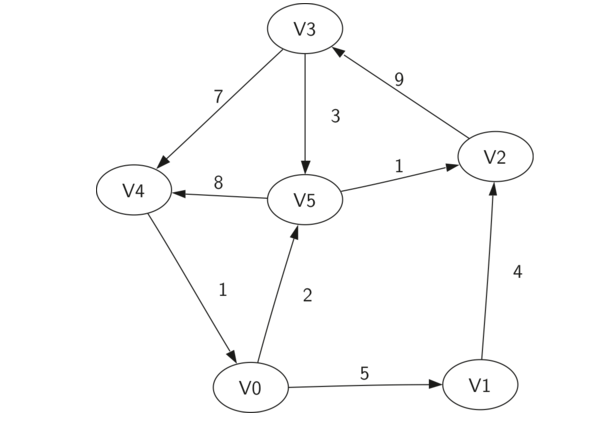
可以将下面的图表示为六个顶点的集合：
\(V = \{ V0,V1,V2,V3,V4,V5\}\)
和 9 条边的集合：
\(E = \{ (v0,v1,5),(v1,v2,4),(v2,v3,9),(v3,v4,7),(v4,v0,1),(v0,v5,2),(v5,v4,8),(v3,v5,3),(v5,v2,1)\}\)

路径##

图中的路径是由边连接的顶点序列。
从 V3 到 V1 的路径是顶点序列 :\((V3,V4,V0,V1)\)，边是：\(\{ (v3,v4,7),(v4,v0,1),(v0,v1,5)\}\)。

循环##

有向图中的循环是在同一顶点开始和结束的路径。上图中路径\(\left( {V5,V2,V3,V5} \right)\)。是一个循环。没有循环的图形称为非循环图形。没有循环的有向图称为有向无环图或 DAG。

图的抽象数据类型

操作	描述
Graph()	创建一个新的空图
addVertex(vert)	向图中添加一个顶点实例
addEdge(fromVert, toVert)	向连接两个顶点的图添加一个新的有向边
addEdge(fromVert, toVert, weight)	向连接两个顶点的图添加一个新的加权的有向边
getVertex(vertKey)	在图中找到名为 vertKey 的顶点
getVertices()	返回图中所有顶点的列表
in	返回 True 如果 vertex in graph 里给定的顶点在图中，否则返回False