二叉搜索树

二叉搜索树

左子树中的所有键小于根中的键，右子树中的所有键都大于根。该属性适用于每个父级和子级。

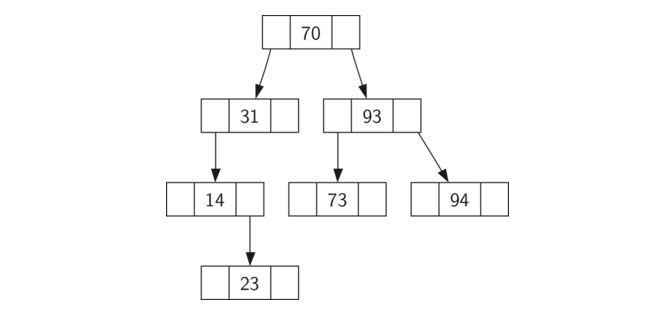
二叉搜索树操作

操作	描述
Map()	创建一个新的空 map
put(key，val)	向 map 中添加一个新的键值对，如果键已经在 map 中，那么用新值替换旧值
get(key)	给定一个键，返回存储在 map 中的值，否则为 None
del	使用 del map[key] 形式的语句从 map 中删除键值对
len()	返回存储在映射中的键值对的数量
in	返回 True 如果给定的键在 map 中

二叉搜索树实现

辅助类TreeNode

class TreeNode:
    def __init__(self,key,val,left=None,right=None,parent=None):
        self.key = key
        self.payload = val
        self.leftChild = left
        self.rightChild = right
        self.parent = parent

    def hasLeftChild(self):
        return self.leftChild

    def hasRightChild(self):
        return  self.rightChild

    def isLeftChild(self):
        return  self.parent and self.parent.leftChild == self

    def isRightChild(self):
        return self.parent and self.parent.rightChild == self

    def isRoot(self):
        return  not self.parent

    def isLeaf(self):
        return  not (self.rightChild or self.rightChild)

    def hasAnyChildren(self):
        return self.rightChild or self.leftChild

    def hasBothChildren(self):
        return  self.leftChild and self.rightChild


    def replaceNodeData(self,key,value,lc,rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self

二叉搜索树类BinarySearchTree

class BinarySearchTree:

    def __init__(self):
        self.root = None
        self.size = 0

    def length(self):
        return self.size

    def __len__(self):
        return self.size

put方法

接下来要实现put方法，此方法将检查树是否已具有根。如果没有根，那么 put 将创建一个新的 TreeNode 并将其做为树的根。如果根节点已经就位，则 put 调用私有递归辅助函数_put根据以下算法搜索树：

• 从树的根开始，搜索二叉树，将新键与当前节点中的键进行比较。如果新键小于当前节点，则搜索左子树。如果新键大于当前节点，则搜索右子树。
• 当没有左（或右）孩子要搜索时，我们在树中找到应该建立新节点的位置。
• 要向树中添加节点，请创建一个新的 TreeNode 对象，并将对象插入到上一步发现的节点。

插入过程可以参考下图：

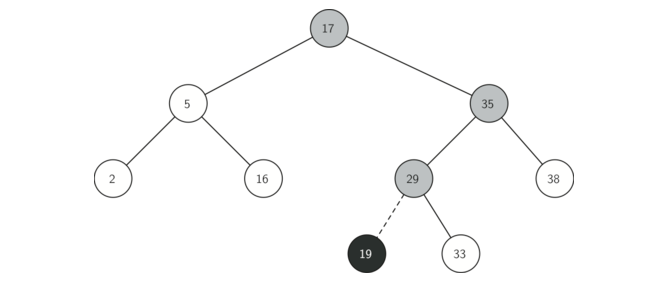
def put(self,key,val):
    if self.root:
        self._put(key,val,self.root)
    else:
        self.root = TreeNode(key,val)
    self.size = self.size + 1

def _put(self,key,val,currentNode):
    if key < currentNode.key:
        if currentNode.hasLeftChild():
               self._put(key,val,currentNode.leftChild)
        else:
               currentNode.leftChild = TreeNode(key,val,parent=currentNode)
    else:
        if currentNode.hasRightChild():
               self._put(key,val,currentNode.rightChild)
        else:
               currentNode.rightChild = TreeNode(key,val,parent=currentNode)

当 put 方法定义后，我们可以通过使用 __setitem__ 方法调用put 方法来重载赋值的 [] 运算符。这使得我们可以编写像myZipTree['Plymouth'] = 55446 这样的 Python 语句，就像 Python 字典一样。

def __setitem__(self,k,v):
    self.put(k,v)

get方法

get 方法比 put 方法更容易，因为它只是递归地搜索树，直到它到达不匹配的叶节点或找到匹配的键。当找到匹配的键时，返回存储在节点的有效载荷中的值。

def get(self,key):
    if self.root:
        res = self._get(key,self.root)
        if res:
               return res.payload
        else:
               return None
    else:
        return None

def _get(self,key,currentNode):
    if not currentNode:
        return None
    elif currentNode.key == key:
        return currentNode
    elif key < currentNode.key:
        return self._get(key,currentNode.leftChild)
    else:
        return self._get(key,currentNode.rightChild)

通过实现 __getitem__ 方法，我们可以编写一个类似于访问字典的 Python 语句，而实际上我们使用的是二叉搜索树，例如 z = myZipTree ['Fargo']。

def __getitem__(self,key):
    return self.get(key)

使用 get ，我们可以通过为 BinarySearchTree 写一个__contains__ 方法来实现 in 操作。 __contains__ 方法将简单地调用 get 并在get返回值时返回 True，如果返回 None 则返回 False。

def __contains__(self,key):
    if self._get(key,self.root):
        return True
    else:
        return False

delete方法

• 如果树只有一个节点，这意味着我们删除树的根，但是我们仍然必须检查以确保根的键匹配要删除的键。
• 如果树具有多个节点，我们使用 _get 方法搜索以找到需要删除的TreeNode。
• 在任一情况下，如果未找到键，del 操作符将引发错误。

def delete(self,key):
   if self.size > 1:
      nodeToRemove = self._get(key,self.root)
      if nodeToRemove:
          self.remove(nodeToRemove)
          self.size = self.size-1
      else:
          raise KeyError('Error, key not in tree')
   elif self.size == 1 and self.root.key == key:
      self.root = None
      self.size = self.size - 1
   else:
      raise KeyError('Error, key not in tree')

def __delitem__(self,key):
    self.delete(key)

一旦我们找到了我们要删除的键的节点，我们必须考虑三种情况：

• 要删除的节点没有子节点
• 要删除的节点只有一个子节点
• 要删除的节点有两个子节点

要删除的节点没有子节点

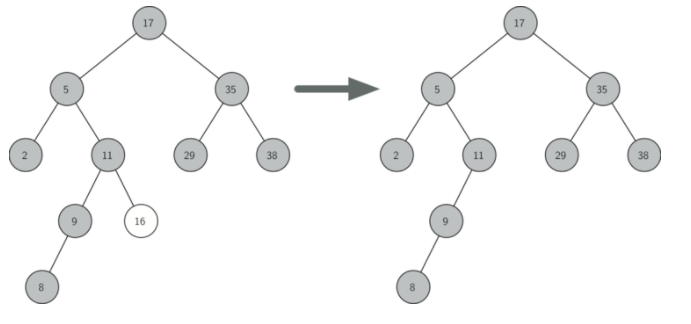
如果当前节点没有子节点，我们需要做的是删除节点并删除对父节点中该节点的引用。 此处的代码如下所示：

if currentNode.isLeaf():
    if currentNode == currentNode.parent.leftChild:
        currentNode.parent.leftChild = None
    else:
        currentNode.parent.rightChild = None

要删除的节点只有一个子节点

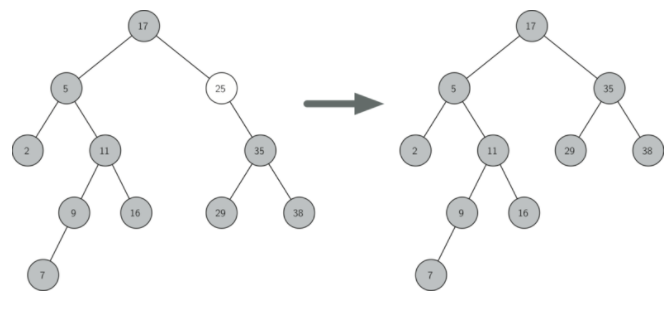
如果一个节点只有一个孩子，那么我们可以简单地促进孩子取代其父。讨论当前节点具有左孩子的情况。决策如下：
(1) 如果当前节点是左子节点，则我们只需要更新左子节点的父引用以指向当前节点的父节点，然后更新父节点的左子节点引用以指向当前节点的左子节点。
(2) 如果当前节点是右子节点，则我们只需要更新左子节点的父引用以指向当前节点的父节点，然后更新父节点的右子节点引用以指向当前节点的左子节点。
(3) 如果当前节点没有父级，则它是根。在这种情况下，我们将通过在根上调用replaceNodeData 方法来替换 key，payload，leftChild 和 rightChild 数据。

else: # this node has one child
   if currentNode.hasLeftChild():
      if currentNode.isLeftChild():
          currentNode.leftChild.parent = currentNode.parent
          currentNode.parent.leftChild = currentNode.leftChild
      elif currentNode.isRightChild():
          currentNode.leftChild.parent = currentNode.parent
          currentNode.parent.rightChild = currentNode.leftChild
      else:
          currentNode.replaceNodeData(currentNode.leftChild.key,
                             currentNode.leftChild.payload,
                             currentNode.leftChild.leftChild,
                             currentNode.leftChild.rightChild)
   else:
      if currentNode.isLeftChild():
          currentNode.rightChild.parent = currentNode.parent
          currentNode.parent.leftChild = currentNode.rightChild
      elif currentNode.isRightChild():
          currentNode.rightChild.parent = currentNode.parent
          currentNode.parent.rightChild = currentNode.rightChild
      else:
          currentNode.replaceNodeData(currentNode.rightChild.key,
                             currentNode.rightChild.payload,
                             currentNode.rightChild.leftChild,
                             currentNode.rightChild.rightChild)

要删除的节点有两个子节点

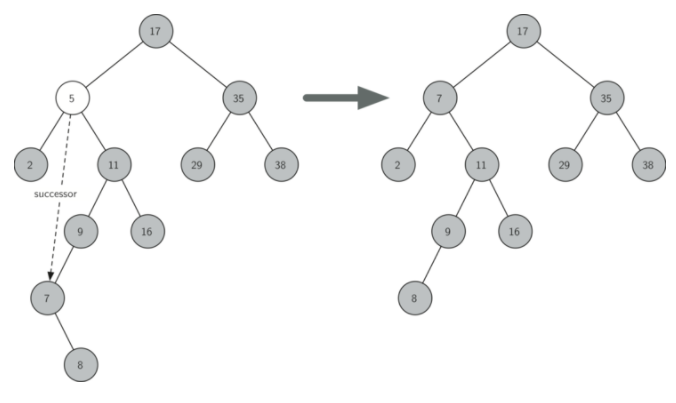
elif currentNode.hasBothChildren(): #interior
        succ = currentNode.findSuccessor()
        succ.spliceOut()
        currentNode.key = succ.key
        currentNode.payload = succ.payload

我们使用辅助方法findSuccessor 和 findMin 来找到后继。 要删除后继，我们使用spliceOut 方法。 我们使用 spliceOut 的原因是它直接找到我们想要拼接的节点，并做出正确的更改。 我们可以递归调用删除，但是我们将浪费时间重新搜索关键节点。
找到后继的代码是 TreeNode 类的一个方法。在寻找接班人时，有三种情况需要考虑：
(1) 如果节点有右子节点，则后继节点是右子树中的最小的键。
(2) 如果节点没有右子节点并且是父节点的左子节点，则父节点是后继节点。
(3) 如果节点是其父节点的右子节点，并且它本身没有右子节点，则此节点的后继节点是其父节点的后继节点，不包括此节点。
调用 findMin 方法来查找子树中的最小键。任何二叉搜索树中的最小值键是树的最左子节点。因此，findMin 方法简单地循环子树的每个节点中的 leftChild 引用，直到它到达没有左子节点的节点。

def findSuccessor(self):
    succ = None
    if self.hasRightChild():
        succ = self.rightChild.findMin()
    else:
        if self.parent:
               if self.isLeftChild():
                   succ = self.parent
               else:
                   self.parent.rightChild = None
                   succ = self.parent.findSuccessor()
                   self.parent.rightChild = self
    return succ

def findMin(self):
    current = self
    while current.hasLeftChild():
        current = current.leftChild
    return current

def spliceOut(self):
    if self.isLeaf():
        if self.isLeftChild():
               self.parent.leftChild = None
        else:
               self.parent.rightChild = None
    elif self.hasAnyChildren():
        if self.hasLeftChild():
               if self.isLeftChild():
                  self.parent.leftChild = self.leftChild
               else:
                  self.parent.rightChild = self.leftChild
               self.leftChild.parent = self.parent
        else:
               if self.isLeftChild():
                  self.parent.leftChild = self.rightChild
               else:
                  self.parent.rightChild = self.rightChild
               self.rightChild.parent = self.parent

二叉树的 inorder 迭代器

Python 为我们提供了一个非常强大的函数，在创建迭代器时使用。该函数称为yield 。 yield 类似于 return，因为它向调用者返回一个值。然而，yield 采取冻结函数状态的附加步骤，使得下一次调用函数时，它从其早先停止的确切点继续执行。创建可以迭代的对象的函数称为生成函数。

def __iter__(self):
   if self:
      if self.hasLeftChild():
             for elem in self.leftChild:
                yield elem
      yield self.key
      if self.hasRightChild():
             for elem in self.rightChild:
                yield elem

完整代码

# 树节点类
class TreeNode:
    # 初始化一个树节点，需要键、值、左子树、右子树、父树
    def __init__(self, key, val, left=None, right=None, parent=None):
        self.key = key
        self.payload = val
        self.leftChild = left
        self.rightChild = right
        self.parent = parent

    # 判断是否有左孩子
    def hasLeftChild(self):
        return self.leftChild

    # 判断是否有右孩子
    def hasRightChild(self):
        return self.rightChild

    # 判断是不是左孩子
    def isLeftChild(self):
        return self.parent and self.parent.leftChild == self

    # 判断是不是右孩子
    def isRightChild(self):
        return self.parent and self.parent.rightChild == self

    # 判断是不是根节点
    def isRoot(self):
        return not self.parent

    # 判断是不是叶节点
    def isLeaf(self):
        return not (self.rightChild or self.leftChild)

    # 判断是不是有子节点
    def hasAnyChildren(self):
        return self.rightChild or self.leftChild

    # 判断是不是同时具有左右子节点
    def hasBothChildren(self):
        return self.rightChild and self.leftChild

    # 替换一个节点
    def replaceNodeData(self, key, value, lc, rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self


# 二叉树
class BinarySearchTree:
    # 初始化一个二叉树
    def __init__(self):
        self.root = None
        self.size = 0

    # 返回一颗树中节点的个数
    def length(self):
        return self.size

    def __len__(self):
        return self.size

    #  向树中插入一个节点
    def put(self, key, val):
        # 原来的树存在根
        if self.root:
            self._put(key, val, self.root)
        # 插入的节点将作为根
        else:
            self.root = TreeNode(key, val)
        self.size = self.size + 1

    # 插入节点
    def _put(self, key, val, currentNode):
        # 如果要插入的节点key小于当前节点的key，向当前节点的左子树寻找位置
        if key < currentNode.key:
            # 如果当前节点已经有左子树，那么就要在当前节点的左子树中继续递归寻找要插入节点的位置
            if currentNode.hasLeftChild():
                self._put(key, val, currentNode.leftChild)
            else:
                # 当前节点已经没有左子树，那么就可以在这个位置插入节点
                currentNode.leftChild = TreeNode(key, val, parent=currentNode)
        # 如果要插入的节点key大于当前节点的key，向当前节点的右子树寻找位置
        else:
            # 如果当前节点已经有右子树，那么就要在当前节点的右子树中继续递归寻找要插入节点的位置
            if currentNode.hasRightChild():
                self._put(key, val, currentNode.rightChild)
            else:
                # 当前节点已经没有右子树，那么就可以在这个位置插入节点
                currentNode.rightChild = TreeNode(key, val, parent=currentNode)

    # 采用类似字典的形式插入键-值
    def __setitem__(self, k, v):
        self.put(k, v)

    # 根据键获取值
    def get(self, key):
        # 若树存在
        if self.root:
            # 按照键查找节点
            res = self._get(key, self.root)
            if res:
                # 找到节点后，返回它的值
                return res.payload
            else:
                return None
        # 树不存在
        else:
            return None

    # 按照键查找节点
    def _get(self, key, currentNode):
        # 节点不存在，返回None
        if not currentNode:
            return None
        # 若当前节点的键正好是要查找的，返回节点
        elif currentNode.key == key:
            return currentNode
        # 如果要查找的键小于当前节点的键则继续在当前节点的左子树中查找
        elif key < currentNode.key:
            return self._get(key, currentNode.leftChild)
        # 如果要查找的键大于当前节点的键则继续在当前节点的右子树中查找
        else:
            return self._get(key, currentNode.rightChild)

    # 以字典的形式获取键-值
    def __getitem__(self, key):
        return self.get(key)

    # 判断树中是否存在某个键
    def __contains__(self, key):
        if self._get(key, self.root):
            return True
        else:
            return False

    # 删除一个节点
    def delete(self, key):
        # 如果当前的树节点个数大于1
        if self.size > 1:
            # 根据键获取要删除的节点
            nodeToRemove = self._get(key, self.root)
            if nodeToRemove:
                self.remove(nodeToRemove)
                self.size = self.size - 1
            else:
                raise KeyError('Error, key not in tree')
        # 如果当前的树节点个数等于1，并且当前的根节点就是要查找的节点
        elif self.size == 1 and self.root.key == key:
            self.root = None
            self.size = self.size - 1
        # 如果当前的树节点个数等于1，并且当前的根节点并不是要查找的节点
        else:
            raise KeyError('Error, key not in tree')

    # 以字典的形式删除键-值对
    def __delitem__(self, key):
        self.delete(key)

    # 移除节点
    def remove(self, currentNode):
        # 如果当前的节点是叶节点
        if currentNode.isLeaf():  # leaf
            # 如果是左子树，直接删除
            if currentNode == currentNode.parent.leftChild:
                currentNode.parent.leftChild = None
            # 如果是右子树，直接删除
            else:
                currentNode.parent.rightChild = None
        # 当前的节点左右子树都存在
        elif currentNode.hasBothChildren():  # interior
            succ = currentNode.findSuccessor()
            succ.spliceOut()
            currentNode.key = succ.key
            currentNode.payload = succ.payload
        # 当前的节点只有一个节点，直接移除，并且采用子节点顶替父节点的方法实现剩余的连接
        else:  # this node has one child
            # 如果拥有的节点是左子节点
            if currentNode.hasLeftChild():
                # 当前节点是左节点
                if currentNode.isLeftChild():
                    # 当前节点的左子节点的父节点更新为当前节点的父节点
                    currentNode.leftChild.parent = currentNode.parent
                    # 当前节点的父节点的左子节点更新为当前节点的左子节点
                    currentNode.parent.leftChild = currentNode.leftChild
                # 当前节点是右子节点
                elif currentNode.isRightChild():
                    # 当前节点的左子节点的父节点更新为当前节点的父节点
                    currentNode.leftChild.parent = currentNode.parent
                    # 当前节点的父节点的左子节点更新为当前节点的右子节点
                    currentNode.parent.rightChild = currentNode.leftChild
                # 当前节点是根节点
                else:
                    # 直接使用左子节点替换当前的节点
                    currentNode.replaceNodeData(currentNode.leftChild.key,
                                                currentNode.leftChild.payload,
                                                currentNode.leftChild.leftChild,
                                                currentNode.leftChild.rightChild)
            # 如果拥有的节点是右子节点
            else:
                # 当前节点是左节点
                if currentNode.isLeftChild():
                    # 当前节点的右子节点的父节点更新为当前节点的父节点
                    currentNode.rightChild.parent = currentNode.parent
                    # 当前节点的父节点的左子节点更新为当前节点的右子节点
                    currentNode.parent.leftChild = currentNode.rightChild
                # 当前节点是右子节点
                elif currentNode.isRightChild():
                    # 当前节点的右子节点的父节点更新为当前节点的父节点
                    currentNode.rightChild.parent = currentNode.parent
                    # 当前节点的父节点的右子节点更新为当前节点的右子节点
                    currentNode.parent.rightChild = currentNode.rightChild
                # 当前节点是根节点
                else:
                    # 直接使用右子节点替换当前的节点
                    currentNode.replaceNodeData(currentNode.rightChild.key,
                                                currentNode.rightChild.payload,
                                                currentNode.rightChild.leftChild,
                                                currentNode.rightChild.rightChild)
    # 寻找后继节点
    def findSuccessor(self):
        succ = None
        # 如果当前节点存在右子节点，那么继任者就是右子节点中最小的节点
        if self.hasRightChild():
            succ = self.rightChild.findMin()
        # 如果没有右子节点
        else:
            # 当前节点存在父节点
            if self.parent:
                # 如当前节点是左子节点
                if self.isLeftChild():
                    succ = self.parent
                # 如当前节点是右子节点
                else:
                    self.parent.rightChild = None
                    succ = self.parent.findSuccessor()
                    self.parent.rightChild = self
        return succ


    def spliceOut(self):
        # 如果是叶节点
        if self.isLeaf():
            if self.isLeftChild():
                self.parent.leftChild = None
            else:
                self.parent.rightChild = None
        # 如果有子节点
        elif self.hasAnyChildren():
            # 拥有左子节点
            if self.hasLeftChild():
                if self.isLeftChild():
                    self.parent.leftChild = self.leftChild
                else:
                    self.parent.rightChild = self.leftChild
                self.leftChild.parent = self.parent
            # 拥有右子节点
            else:
                if self.isLeftChild():
                    self.parent.leftChild = self.rightChild
                else:
                    self.parent.rightChild = self.rightChild
                self.rightChild.parent = self.parent


    # 查找最小节点，也就是最左节点
    def findMin(self):
        current = self
        while current.hasLeftChild():
            current = current.leftChild
        return current


mytree = BinarySearchTree()
mytree[3] = "red"
mytree[4] = "blue"
mytree[6] = "yellow"
mytree[2] = "at"

print(mytree[6])
print(mytree[2])