二叉堆
二叉堆
优先级队列的作用就像一个队列,在优先级队列中,队列中的项的逻辑顺序由它们的优先级确定:最高优先级项在队列的前面,最低优先级的项在后面。因此,当你将项排入优先级队列时,新项可能会一直移动到前面。
实现优先级队列的经典方法是使用称为二叉堆的数据结构。二叉堆将允许我们在 \(O(logn)\)中排队和取出队列。
二叉堆有两个常见的变体:最小堆(其中最小的键总是在前面)和最大堆(其中最大的键值总是在前面)。
二叉堆操作
| 操作 | 描述 |
|---|---|
| BinaryHeap() | 创建一个新的,空的二叉堆 |
| insert(k) | 向堆添加一个新项 |
| findMin() | 返回具有最小键值的项,并将项留在堆中 |
| delMin() | 返回具有最小键值的项,从堆中删除该项 |
| isEmpty() | 如果堆是空的,返回 true,否则返回 false |
| size() | 返回堆中的项数 |
| buildHeap(list) | 从键列表构建一个新的堆 |
二叉堆的属性
堆的结构属性
为了使我们的堆有效地工作,我们将利用二叉树的对数性质来表示我们的堆。 为了保证对数性能,我们必须保持树平衡。
平衡二叉树在根的左和右子树中具有大致相同数量的节点。
在我们的堆实现中,我们通过创建一个 完整二叉树 来保持树平衡。一个完整的二叉树是一个树,其中每个层都有其所有的节点,除了树的最底层,从左到右填充。如下图所示:

完整二叉树的另一个有趣的属性是,我们可以使用单个列表来表示它。 我们不需要使用节点和引用,甚至列表的列表。因为树是完整的,父节点的左子节点(在位置 p 处)是在列表中位置 2p 中找到的节点。 类似地,父节点的右子节点在列表中的位置 2p + 1。为了找到树中任意节点的父节点,我们可以简单地使用Python 的整数除法。 假定节点在列表中的位置 n,则父节点在位置 n/2。
堆的排序属性
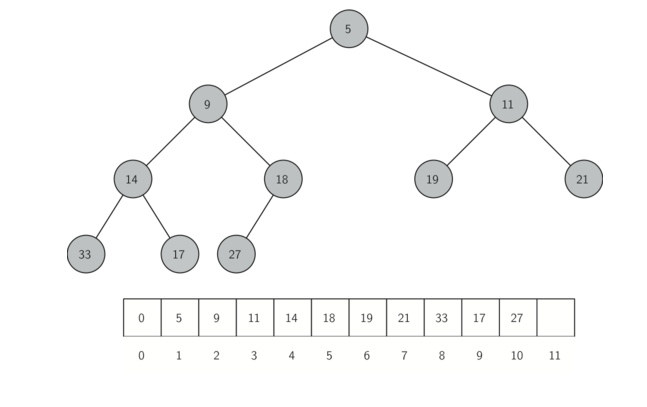
我们用于堆中存储项的方法依赖于维护堆的排序属性。 堆的排序属性如下:在堆中,对于具有父 p 的每个节点 x,p 中的键小于或等于 x 中的键。
具有堆顺序属性的完整二叉树如下图所示:
堆实现
构造一个空的二叉堆
一个空的二叉堆有一个单一的零作为 heapList 的第一个元素,这个零只是放那里,用于以后简单的整数除法。
class BinHeap:
def __init__(self):
self.heapList = [0]
self.currentSize = 0
堆中插入项
将项添加到列表中最简单,最有效的方法是将项附加到列表的末尾。 这样就可以维护完整的树属性。但可能违反堆的顺序属性。可以编写一个方法,通过比较新添加的项与其父项,我们可以重新获得堆的顺序属性。 如果新添加的项小于其父项,则我们可以将项与其父项交换。

#二叉堆中插入元素
def insert(self,k):
self.heapList.append(k)
self.currentSize += 1
self.percUp(self.currentSize)
def percUp(self,i):
while i // 2 > 0:
#子节点与父节点比较,子节点小则与父节点交换位置
if self.heapList[i] < self.heapList[i //2]:
tmp = self.heapList[i //2]
self.heapList[i // 2] = self.heapList[i]
self.heapList[i] = tmp
i = i //2
删除最小值
因为堆属性要求树的根是树中的最小项,所以找到最小项很容易。delMin 的难点在根被删除后恢复堆结构和堆顺序属性。
我们可以分两步恢复我们的堆:
- 我们将通过获取列表中的最后一个项并将其移动到根位置来恢复根项,保持我们的堆结构属性。
- 但是,我们可能已经破坏了我们的二叉堆的堆顺序属性。我们通过将新的根节点沿着树向下推到其正确位置来恢复堆顺序属性。

#返回堆中最小值
def delMin(self):
#堆顶值就是最小值,将其返回
retval = self.heapList[1]
self.heapList[1] = self.heapList[self.currentSize]
self.currentSize -= 1
self.heapList.pop()
self.percDown(1)
return retval
#自顶向下,比较父节点与子节点的大小,保持堆的顺序性
def percDown(self,i):
while (i * 2) <= self.currentSize:
mc = self.minChild(i)
if self.heapList[i] > self.heapList[mc]:
tmp = self.heapList[i]
self.heapList[i] = self.heapList[mc]
self.heapList[mc] = tmp
i = mc
#返回子节点中值较小的节点的索引
def minChild(self,i):
#如果没有右子节点,则直接返回左子节点的索引值
if i * 2 + 1 > self.currentSize:
return i *2
#如果存在右子节点,则取两者中较小的值,返回其索引
else:
if self.heapList[i*2] < self.heapList[i*2+1]:
return i * 2
else:
return i * 2 + 1
从列表构建二叉堆
def buildHeap(self,alist):
i = len(alist) // 2
self.currentSize = len(alist)
self.heapList = [0] + alist[:]
while(i > 0):
self.percDown(i)
i = i - 1

完整代码
# 二叉堆
class BinHeap:
def __int__(self):
self.heapList = [0]
self.currentSize = 0
#二叉堆中插入元素
def insert(self,k):
self.heapList.append(k)
self.currentSize += 1
self.percUp(self.currentSize)
def percUp(self,i):
while i // 2 > 0:
#子节点与父节点比较,子节点小则与父节点交换位置
if self.heapList[i] < self.heapList[i //2]:
tmp = self.heapList[i //2]
self.heapList[i // 2] = self.heapList[i]
self.heapList[i] = tmp
i = i //2
#返回堆中最小值
def delMin(self):
#堆顶值就是最小值,将其返回
retval = self.heapList[1]
self.heapList[1] = self.heapList[self.currentSize]
self.currentSize -= 1
self.heapList.pop()
self.percDown(1)
return retval
#自顶向下,比较父节点与子节点的大小,保持堆的顺序性
def percDown(self,i):
while (i * 2) <= self.currentSize:
mc = self.minChild(i)
if self.heapList[i] > self.heapList[mc]:
tmp = self.heapList[i]
self.heapList[i] = self.heapList[mc]
self.heapList[mc] = tmp
i = mc
#返回子节点中值较小的节点的索引
def minChild(self,i):
#如果没有右子节点,则直接返回左子节点的索引值
if i * 2 + 1 > self.currentSize:
return i *2
#如果存在右子节点,则取两者中较小的值,返回其索引
else:
if self.heapList[i*2] < self.heapList[i*2+1]:
return i * 2
else:
return i * 2 + 1
def buildHeap(self,alist):
i = len(alist) // 2
self.currentSize = len(alist)
self.heapList = [0] + alist[:]
while(i > 0):
self.percDown(i)
i = i - 1
测试:
bh = BinHeap()
bh.buildHeap([9,5,6,2,3])
print(bh.delMin())
print(bh.delMin())
print(bh.delMin())
print(bh.delMin())
print(bh.delMin())
输出:
2
3
5
6
9
时间复杂度为\(O(n)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号