分析树
分析树
数学表达式作为分析树，例如 （（7 + 3）*（5-2））：
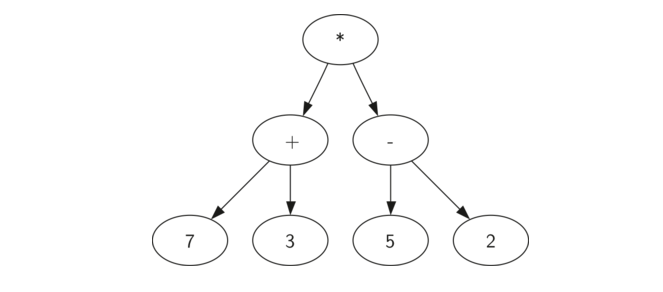
树的层次结构有助于我们了解整个表达式的求值顺序。在我们计算顶层乘法之前，我们必须计算子树中的加法和减法。作为左子树的加法结果为10。减法，即右子树，计算结果为3。
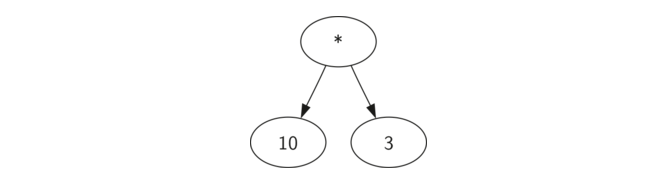
构建分析树的第一步是将表达式字符串拆分成符号列表。 有四种不同的符号要考虑：左括号，右括号，运算符和操作数。
分析树构建规则
我们可以定义四个规则如下：
- 如果当前符号是 '('，添加一个新节点作为当前节点的左子节点，并下降到左子节点。
- 如果当前符号在列表 ['+'，' - '，'/'，'*'] 中，请将当前节点的根值设置为由当前符号表示的运算符。 添加一个新节点作为当前节点的右子节点，并下降到右子节点。
- 如果当前符号是数字，请将当前节点的根值设置为该数字并返回到父节点。
- 如果当前令牌是 ')'，则转到当前节点的父节点。
例如表达式（3+（4 * 5）），把这个表达式解析成下面的字符标记列表 ['('，'3'，'+'，'('，'4'，'*'，'5'，')'，')']，分析树构建过程按照上面的规则可以分解为：
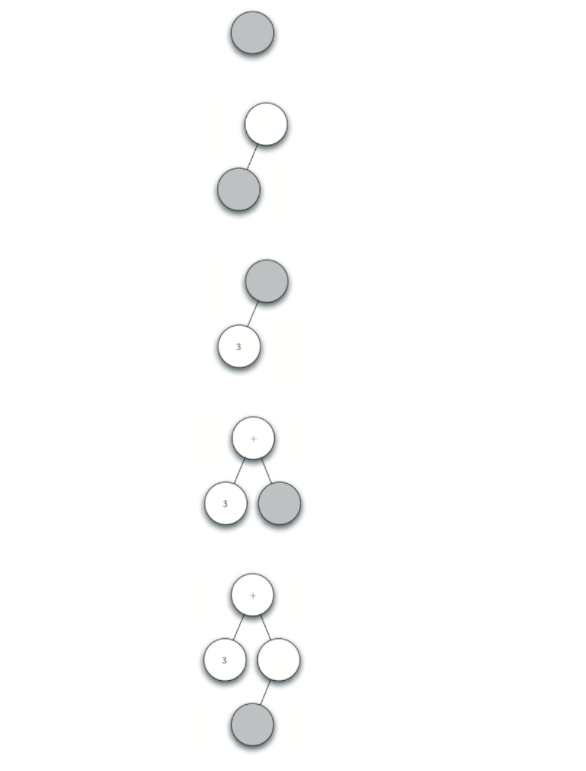
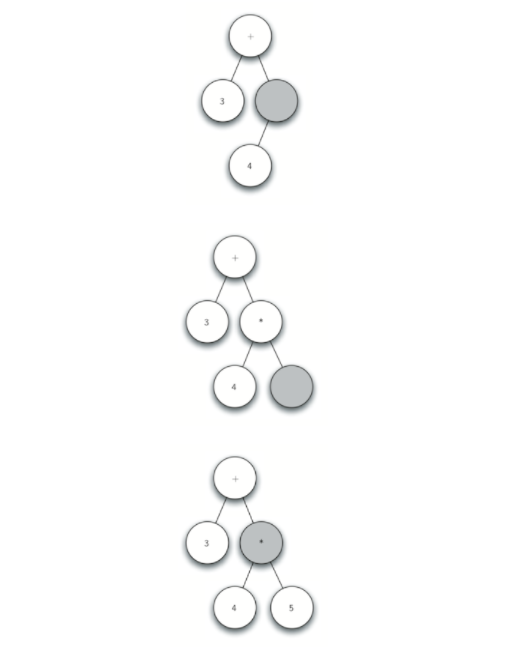
按照上述的方法，我们知道需要记住当前跟根节点的位置，以便返回，我们借助栈来实现，每次向下创建子节点的时候，将父节点入栈，每次返回到父节点的时候，我们从栈中弹出一个元素。
分析树实现
from stack import Stack
from binaryTree import *
def buildParseTree(fpexp):
#分割字符串
fplist = fpexp.split()
#创建一个辅助栈
pSack = Stack()
#创建一个空的根节点并且标记好，以便最终返回
eTree = BinaryTree('')
#将当前的根节点入栈
pSack.push(eTree)
#创建一个根节点的标志
currentTree = eTree
for i in fplist:
#如果当前是左括号，那么新增加一个左子节点，将当前节点移动到左子节点
if i == '(':
currentTree.insertLeft('')
pSack.push(currentTree)
currentTree = currentTree.getLeftChild()
# 如果当前的项是数字，那么就将当前节点设置为这个数字，并且将当前节点移动到父节点
elif i not in ['+','-','*','/',')']:
currentTree.setRootVal(int(i)) #转换成整型
parent = pSack.pop()
currentTree = parent
#如果当前的项是运算符，那么就将当前节点设置成这个运算符，并且新建一个右子节点，当前节点移动到这个新建的右子节点
elif i in ['+','-','*','/']:
currentTree.setRootVal(i)
currentTree.insertRight('')
pSack.push(currentTree)
currentTree = currentTree.getRightChild()
elif i == ')':
currentTree = pSack.pop()
else:
raise ValueError
return eTree
测试：
pt = buildParseTree("( 3 + ( 4 * 5 ) )")
print("前序遍历的结果：")
pt.preorder()
print("中序遍历的结果：")
pt.inorder()
print("后序遍历的结果：")
pt.postorder()
输出：
前序遍历的结果：
+
3
*
4
5
中序遍历的结果：
3
+
4
*
5
后序遍历的结果：
3
4
5
*
+
参考:
