[数据结构与算法] 树状数组

链接：树状数组_哔哩哔哩 （只有五分钟，多看几遍，就会了）

模板题：P3374 【模板】树状数组 1 - 洛谷

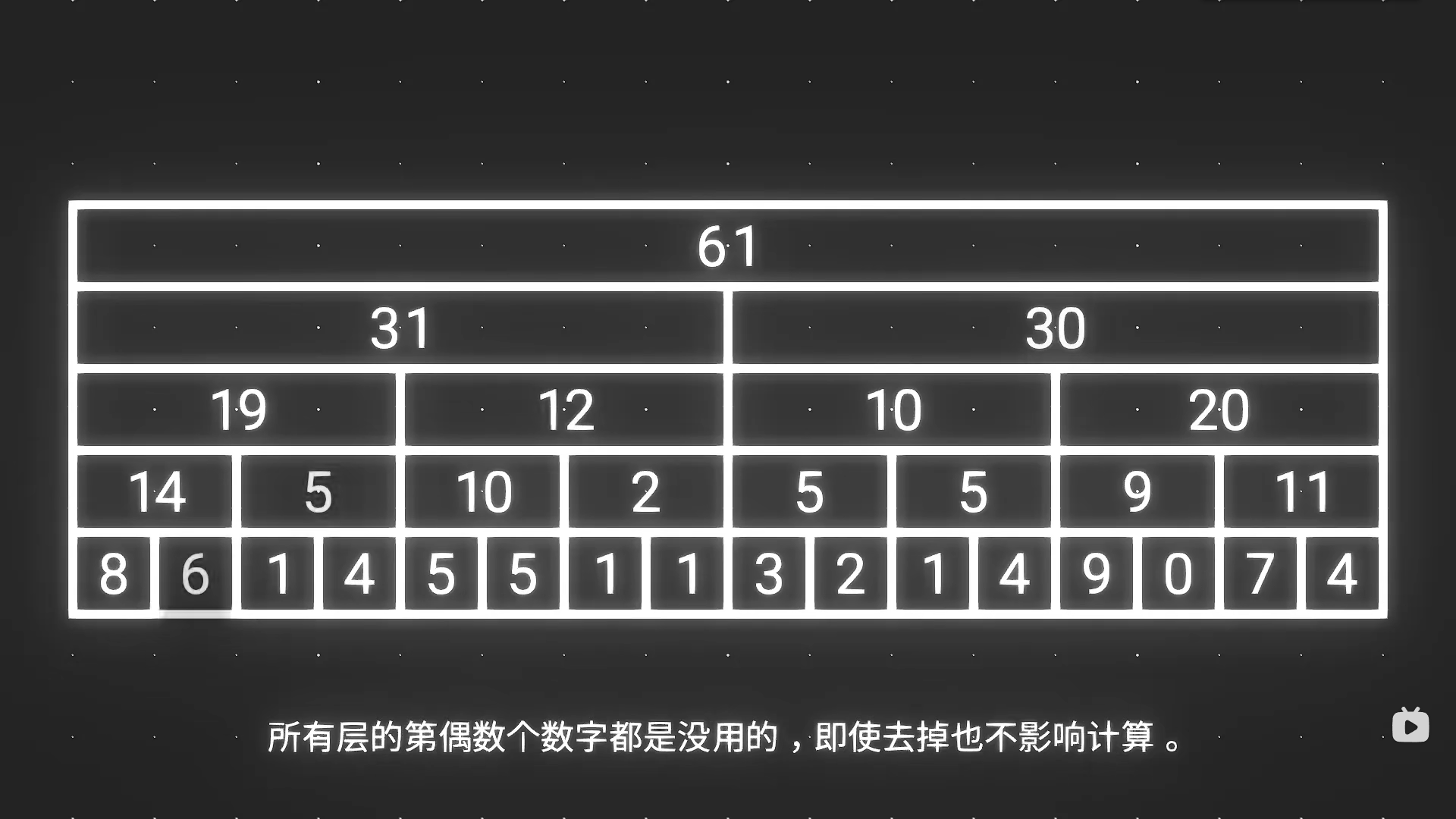
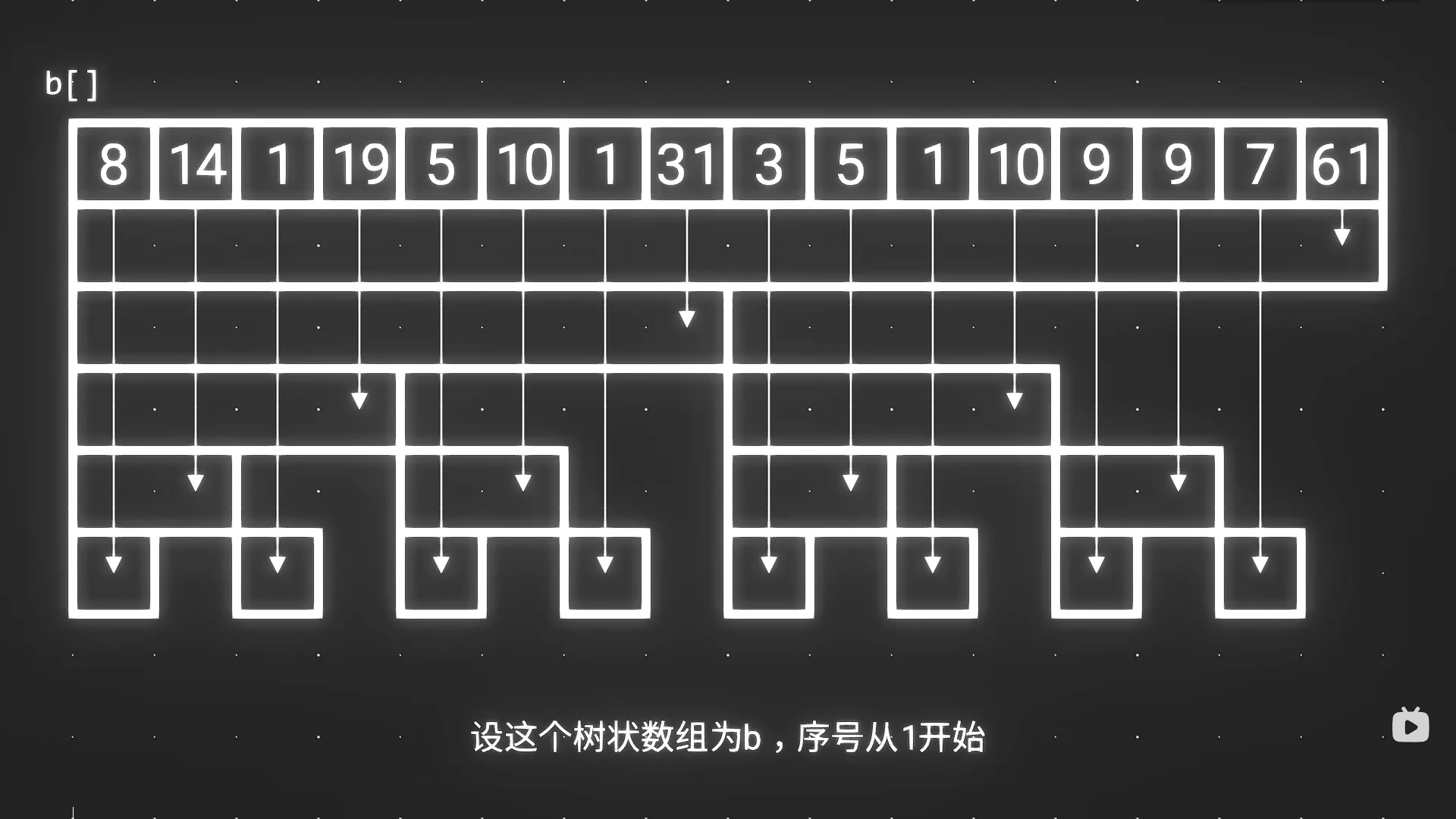
树结构：(上图是完整树结构，下图是树状数组树结构)，代码对这写容易理解。

14.1 作用

• 求前缀和、区间和（跟前缀和的作用一样）；
• 元素修改之后能高效更新：（时间复杂度）
  • 前缀和：$O(log \space n)$；
  • 区间和：$O(log \space n)$；
  • 点更新：$O(log \space n)$；
  • 点查询：$O(log \space n)$；
  • 区间更新：$O(nlog \space n)$；

14.2 性质

• 每层偶数个数字都是没用的，可用于存储上方层的数值（本层序列和下一序列的和）；

• 树状数组中第 pos 个元素所在的序列长度正好为 lowbit(pos)^[1] 且以 pos 结尾的序列，该序列存储的值是 pos 所在的序列的和。因此求 pos 的前缀和的过程就是将 pos 之前的序列值一直累加。根据这个就可以得到 count(int pos) 函数；

• tree[pos] 所在序列的上方的序列，正好就是 tree[pos + lowbit(pos)] ，由于 lowbit(pos) 是 pos 所在序列的长度，因此实际上就是 pos 加上所在序列长度就得到上方序列的值的下标。因此树状数组的更新操作就是更新 pos 所在的序列以及之上的所有序列。由此可得函数 add(int pos, int diff)。

14.2 代码

#include <bits/stdc++.h>
using namespace std;

// 数组下标从1开始，元素初始化为0
vector<int> nums;
vector<int> tree;			// 树状数组，也就是视频中的数组 b

int lowbit(int num) {
    return num & (-num);
}

// 更新值：pos为修改的位置，diff为原本元素需加上的新值
void add(int pos, int diff) {
    int len = nums.size();
    while (pos < len) {
        tree[pos] += diff;
        pos += lowbit(pos);
    }
}

// 求前缀和
long long count(int pos) {
    long long res = 0;
    while (pos) {
        res += tree[pos];
        pos -= lowbit(pos);
    }
    return res;
}

// 求区间和
long long sum(int left, int right) {
    return count(right) - count(left - 1);
}

int main() {
    int n;
    cin >> n;
    nums.resize(n + 1);			// 数组下标从1开始
    tree.resize(n + 1);			// 数组下标从1开始
    for (int i = 1; i <= n; ++i) {	// 注意是i从1到n
        cin >> nums[i];			// 修改的时候可能会需要用nums数组计算差值，然后调用add函数更新，本例中未用到该数组
        add(i, nums[i]);
    }
    for (int i = 1; i <= n; ++i) {	// 输出树状数组
        cout << tree[i] << " ";
    }
    int left, right;
    cout << endl << "输入需要求和的区间：";
    cin >> left >> right;
    cout << sum(left, right) << endl;	// 求区间[left, right]的和
    return 0;
}

注解

---

1. lowbit(int n) 函数就是求出n的最后一个位 1 所代表的数，例如 12 的二进制位 1100 ，则 lowbit(12) 的结果为 4. ↩︎