「HNOI2019」多边形(树形dp)

题目给出的操作和条件都非常抽象，这意味着我们需要极大程度上精简这个问题

环$\rightarrow$序列

首先，我们将环达成$1..n$的序列，每条边就是一个区间，暂且保留所有多边形原本的边

每条边在多边形上都是把区域分成两部分，所以在序列上每条边都是把一个区间$[L,R]$分成$[L,mid],[mid,R]$，直到最后$L+1=R$

\[\ \]

序列$\rightarrow $树

考虑这个分解的过程，事实上就是一个构建二叉树的过程，其中$L+1=R$的节点就是叶子

那么得到一些简单性质$L_{lson}=L_{father},R_{rson}=R_{father},R_{father}>R_{lson},L_{rson}>L_{father}$

根据这四个性质，对于每个$L$，对于每个$R$分别做一下，就能够构造出一棵二叉树了

最后得到的大概是这个样子(对应题目样例1)

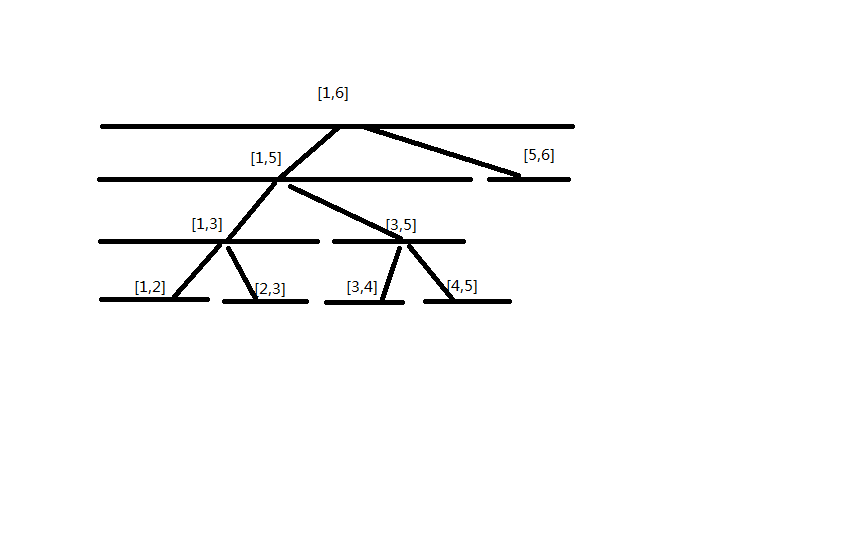
无标题.png

建树代码(这里直接省略了叶子节点)

	W=rd(),n=rd();
	A[++cnt]=(Node){1,n,cnt}; // 加入根
	rep(i,1,n-3) ++cnt,A[cnt].l=rd(),A[cnt].r=rd(),A[cnt].id=cnt; // 加入节点
	rep(i,1,cnt) M[A[i].l][A[i].r]=i;
	sort(A+1,A+cnt+1,cmp1);
	rep(i,1,cnt) {
		int j=i;
		while(j<n && A[j+1].l==A[j].l) ++j;
		rep(k,i,j-1) ls[A[k].id]=A[k+1].id,fa[A[k+1].id]=A[k].id;
		i=j;
	}
	sort(A+1,A+cnt+1,cmp2);
	rep(i,1,cnt) {
		int j=i;
		while(j<n && A[j+1].r==A[j].r) ++j;
		rep(k,i,j-1) rs[A[k].id]=A[k+1].id,fa[A[k+1].id]=A[k].id;
		i=j;
	} // 两次sort确定父子关系
	sort(A+1,A+cnt+1,[&](Node x,Node y){ return x.id<y.id; });
	// 找回原来的顺序

\[\ \]

操作$(a,b,c,d)$

观察上面的这个树

那么一个操作$(a,b,c,d)$可行的条件就是：对于一个非叶子且非根的节点，它是父亲的左儿子

所以可以非常显然地得到，最后得到的所有边就是$[i,i+1]$和$[i,n]$，让一整棵树变成一条右儿子链

\[\ \]

最少操作次数

考虑每一次操作，对于节点$x$，操作它意味着

$x.rson\leftarrow brother$

$father.lson\leftarrow x.lson$

$father.rson\leftarrow x$

把这个节点提上去，自己的左儿子变成父节点的左儿子

可以看到每次操作过后，你的左儿子又需要操作

不用操作的点，只有根节点的右儿子链，因为他们永远不可能成为左儿子

这样我们就知道了最少的操作次数

\[\ \]

最少操作的限制

限制：如果你把一个点$x$操作了，而且$x.father.R\ne n$，那么这一次操作无效，你仍然需要继续被操作

所以每次操作的点，必须满足$x.father.R=n$

\[\ \]

$O(n)$ dp

考虑建出树之后，进行树形dp求得答案

1.点x需要被操作

由于上面的限制，可以发现的是，$x$被操作的时间小于$x.lson,x.rson$，两个儿子之间并没有限制

所以把这个过程转化为合并两边的操作序列，然后在前面接上$x$

2.点x不需要被操作

和上面类似，不接上$x$即可


struct DPNODE{
	int x,y;
	DPNODE(int a=0,int b=1){ x=a,y=b; } 
	friend DPNODE operator + (const DPNODE a,const DPNODE b){
		DPNODE res;
		res.x=a.x+b.x;
		res.y=1ll*a.y*b.y%P*Fac[res.x]%P*Inv[a.x]%P*Inv[b.x]%P;
        // 合并两个序列，组合数
		return res;
	}
};

DPNODE dfs(int p,int k=0){ // k表示当前点选不选
	if(!p) return (DPNODE){0,1};
	DPNODE R=(DPNODE){0,1};
	if(k) R=dfs(rs[p],1)+dfs(ls[p],1),R.x++;
	else R=dfs(rs[p],0)+dfs(ls[p],1); // k下传，只有右儿子链不用被操作
	return R;
}

void Solve() {
	DPNODE res=dfs(1);
	printf("%d %d\n",res.x,res.y);
 	rep(i,1,m){
		int l=rd(),r=rd(),x=M[l][r]; 
		if(A[fa[x]].r==n) {
			DPNODE L=F[x]; L.x--;
			DPNODE t=G[fa[fa[x]]]+L+F[rs[fa[x]]];
			printf("%d %d\n",t.x,t.y);
		} else {
			DPNODE t=F[rs[x]]+F[rs[fa[x]]];
			t.x++;
			t=t+F[ls[x]];
			printf("%d %lld\n",res.x,res.y*qpow(F[fa[x]].y)%P*t.y%P);
		}
	}
}

\[\ \]

动态修改一个点

对于这个点，分成两种情况讨论

$x.father.R\ne n$

意味着改变之后次数不变，唯一变动的就是合并$x.father$的dp值，而向祖先合并的时候，所有的组合数转移都不会发生改变

我们除掉原来$x.father$的$dp$值，乘上新的$dp$值即可

DPNODE t=F[rs[x]]+F[rs[fa[x]]];
t.x++;
t=t+F[ls[x]];// 求出新的dp值
printf("%d %lld\n",res.x,res.y*qpow(F[fa[x]].y,P-2)%P*t.y%P);

$x.father.R=n$

意味着改变这个点，会是操作次数减$1$

这次合并的过程组合数转移会发生变化，但也仅限于$x.father$在根节点的右儿子链上

所以对于每个右儿子链上的点，我们预处理出一个左儿子操作次数减少时的组合数转移$G[x]$，最后补上剩下的部分

namespace pt1{
	DPNODE F[N],G[N];
	DPNODE dfs(int p,int k=0){
		if(!p) return DPNODE();
		DPNODE R;
		if(k){
			DPNODE A=dfs(ls[p],1),B=dfs(rs[p],1);
			R=A+B,R.x++;
		}
		else {
			DPNODE A=dfs(ls[p],1),B=dfs(rs[p],0);
			R=A+B;
			B.x--,B.y=1;
			G[p]=G[fa[p]]+A+B;
		}
		return F[p]=R;
	}
	ll qpow(ll x,ll k=P-2) {
		ll res=1;
		for(;k;k>>=1,x=x*x%P) if(k&1) res=res*x%P;
		return res;
	}

	void Solve() {
		DPNODE res=dfs(1);
		printf("%d %d\n",res.x,res.y);
		rep(i,1,m){
			int l=rd(),r=rd(),x=M[l][r]; 
			if(A[fa[x]].r==n) {
				DPNODE L=F[x]; L.x--;
				DPNODE t=G[fa[fa[x]]]+L+F[rs[fa[x]]];
				printf("%d %d\n",t.x,t.y);
			} else {
				DPNODE t=F[rs[x]]+F[rs[fa[x]]];
				t.x++;
				t=t+F[ls[x]];
				printf("%d %lld\n",res.x,res.y*qpow(F[fa[x]].y)%P*t.y%P);
			}
		}
	}
}

Code总览

#include<bits/stdc++.h>
using namespace std;

#define reg register
typedef long long ll;
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)

#define pb push_back
#define Mod1(x) ((x>=P)&&(x-=P))
#define Mod2(x) ((x<0)&&(x+=P))

template <class T> inline void cmin(T &a,T b){ ((a>b)&&(a=b)); }
template <class T> inline void cmax(T &a,T b){ ((a<b)&&(a=b)); }

char IO;
int rd(){
	int s=0,f=0;
	while(!isdigit(IO=getchar())) if(IO=='-') f=1;
	do s=(s<<1)+(s<<3)+(IO^'0');
	while(isdigit(IO=getchar()));
	return f?-s:s;
}

const int N=1e5+10,P=1e9+7;

int W,n,m;
struct Node{
	int l,r,id;
}A[N];
int cnt,ls[N],rs[N],fa[N];
bool cmp1(Node x,Node y){ return x.l<y.l || (x.l==y.l && x.r>y.r); }
bool cmp2(Node x,Node y){ return x.r<y.r || (x.r==y.r && x.l<y.l); }

int Inv[N],Fac[N];

struct DPNODE{
	int x,y;
	DPNODE(int a=0,int b=1){ x=a,y=b; } 
	friend DPNODE operator + (const DPNODE a,const DPNODE b){
		DPNODE res;
		res.x=a.x+b.x;
		res.y=1ll*a.y*b.y%P*Fac[res.x]%P*Inv[a.x]%P*Inv[b.x]%P;
		return res;
	}
};


map <int,int> M[N];

namespace pt1{
	DPNODE F[N],G[N];
	DPNODE dfs(int p,int k=0){
		if(!p) return DPNODE();
		DPNODE R;
		if(k){
			DPNODE A=dfs(ls[p],1),B=dfs(rs[p],1);
			R=A+B,R.x++;
		}
		else {
			DPNODE A=dfs(ls[p],1),B=dfs(rs[p],0);
			R=A+B;
			B.x--,B.y=1;
			G[p]=G[fa[p]]+A+B;
		}
		return F[p]=R;
	}
	ll qpow(ll x,ll k=P-2) {
		ll res=1;
		for(;k;k>>=1,x=x*x%P) if(k&1) res=res*x%P;
		return res;
	}

	void Solve() {
		DPNODE res=dfs(1);
		printf("%d %d\n",res.x,res.y);
		rep(i,1,m){
			int l=rd(),r=rd(),x=M[l][r]; 
			if(A[fa[x]].r==n) {
				DPNODE L=F[x]; L.x--;
				DPNODE t=G[fa[fa[x]]]+L+F[rs[fa[x]]];
				printf("%d %d\n",t.x,t.y);
			} else {
				DPNODE t=F[rs[x]]+F[rs[fa[x]]];
				t.x++;
				t=t+F[ls[x]];
				printf("%d %lld\n",res.x,res.y*qpow(F[fa[x]].y)%P*t.y%P);
			}
		}
	}
}

namespace pt2{
	int dfs(int p,int k=0){
		if(!p) return 0;
		int cnt=0;
		if(k) {
			++cnt;
			cnt+=dfs(rs[p],1);

			while(ls[p]) {
				p=ls[p];
				++cnt;
				cnt+=dfs(rs[p],1);
			}
		} else {
			cnt+=dfs(rs[p],0);
			while(ls[p]) {
				p=ls[p];
				++cnt;
				cnt+=dfs(rs[p],1);
			}
		}
		return cnt;
	}

	void Solve() {
		int res=dfs(1);
		printf("%d\n",res);
		rep(i,1,m) {
			int l=rd(),r=rd(),x=M[l][r];
			printf("%d\n",res-(A[fa[x]].r==n));
		}
	}
}


namespace pt3{
	DPNODE dfs(int p,int k=0){
		if(!p) return (DPNODE){0,1};
		DPNODE R=(DPNODE){0,1};
		if(k) R=dfs(rs[p],1)+dfs(ls[p],1),R.x++;
		else R=dfs(rs[p],0)+dfs(ls[p],1);
		return R;
	}

	void Solve() {
		DPNODE res=dfs(1);
		printf("%d %d\n",res.x,res.y);
		rep(i,1,m){
			int l=rd(),r=rd(),x=M[l][r];
			l=ls[x],r=rs[x];
			int brother=rs[fa[x]];

			rs[x]=brother,rs[fa[x]]=x;
			ls[x]=r,ls[fa[x]]=l;

			DPNODE res=dfs(1);
			printf("%d %d\n",res.x,res.y);
			
			ls[fa[x]]=x,rs[fa[x]]=brother;
			ls[x]=l,rs[x]=r;
		}
	}
}


int main(){

	Inv[0]=Inv[1]=Fac[0]=Fac[1]=1;
	rep(i,2,N-1) Inv[i]=1ll*(P-P/i)*Inv[P%i]%P,Fac[i]=1ll*Fac[i-1]*i%P;
	rep(i,2,N-1) Inv[i]=1ll*Inv[i]*Inv[i-1]%P;

	W=rd(),n=rd();
	A[++cnt]=(Node){1,n,cnt};
	rep(i,1,n-3) ++cnt,A[cnt].l=rd(),A[cnt].r=rd(),A[cnt].id=cnt;
	rep(i,1,cnt) M[A[i].l][A[i].r]=i;
	sort(A+1,A+cnt+1,cmp1);
	rep(i,1,cnt) {
		int j=i;
		while(j<n && A[j+1].l==A[j].l) ++j;
		rep(k,i,j-1) ls[A[k].id]=A[k+1].id,fa[A[k+1].id]=A[k].id;
		i=j;
	}
	sort(A+1,A+cnt+1,cmp2);
	rep(i,1,cnt) {
		int j=i;
		while(j<n && A[j+1].r==A[j].r) ++j;
		rep(k,i,j-1) rs[A[k].id]=A[k+1].id,fa[A[k+1].id]=A[k].id;
		i=j;
	}
	sort(A+1,A+cnt+1,[&](Node x,Node y){ return x.id<y.id; });
	m=rd();
	if(!W) return pt2::Solve(),0;
	if(n<=11) return pt3::Solve(),0;
	return pt1::Solve(),0;
}

posted @ 2020-05-05 16:09 chasedeath 阅读(254) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

chasedeath

「HNOI2019」多边形(树形dp)

「HNOI2019」多边形(树形dp)

环\(\rightarrow\)序列

序列$\rightarrow $树

操作\((a,b,c,d)\)

最少操作次数

最少操作的限制

\(O(n)\) dp

1.点x需要被操作

2.点x不需要被操作

动态修改一个点

\(x.father.R\ne n\)

\(x.father.R=n\)

Code总览

公告