Splay Tree
\(Splay Tree\)
\(Splay\)是一种非常诡异的数据结构
核心:二叉搜索树
优化:复杂度均摊\(O(nlog n)\)
优化操作:Splay操作
在刚学\(Splay\)时不建议看它的势能分析,因为并没有什么卵用
引入
二叉搜索树(\(BST,Binary Search Tree\)):
核心性质:左儿子小于自己,右儿子大于自己的一棵二叉树
缺陷:对于不同序列树高会呈现$log\ n - n $
\(rotate\)操作
核心:保持BST的大小关系,改变父子关系的一种操作
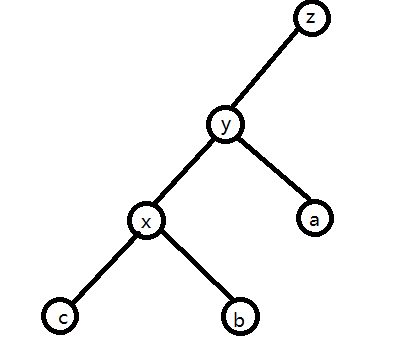
一个正常的BST局部
由父子关系得到 \(c<x<b<y<a<z\)
rotate后
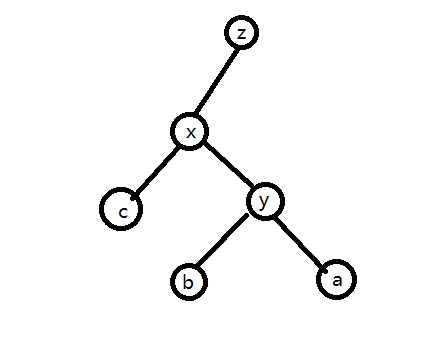
可以看到上面的关系依然成立,并且x变成了y的父亲
这样的rotate操作其实取决于被rotate的节点x是y的左儿子还是右儿子,但是两种情况对称,写起来就是
void rotate(int u){
int f=fa[u],ff=fa[fa[u]],d=son[f][0]==u?0:1,df=son[ff][0]==f?0:1;
son[ff][df]=u;
son[f][d]=son[u][!d];
fa[son[u][!d]]=f;
son[u][!d]=f;
fa[u]=ff,fa[f]=u;
}
\(Splay\)操作
经典的Splay操作有很多分类讨论,这里我们介绍一种精简一点的版本
Splay(u,to),将\(u\)旋转到\(to\)节点的儿子
并且途中经过的链链长减半(特别的,当\(to\)为\(0\)时,即旋转到根)
void Splay(int u,int to){
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(fa[fa[u]]!=to) {
if((son[f][0]==u)^(son[ff][0]==f)) rotate(u);
else rotate(f);
}
rotate(u);
}
if(to==0) rt=u;
}
当\(u\)的祖父不是\(to\)时,考虑两种情况:你与你父亲的作为儿子方向相同和不同(作成图后,可以看到是之字形和一字形)
相同时,如果我们直接多次\(rotate(u)\),会将原来那条\(u\)到\(ff\)的链保留,也就是说,仍然存在存在原来链长,所以我们先\(rotate(f)\),就解决了
另一种就直接两次\(rotate(u)\)即可
\(Splay Tree\)基础操作介绍
事实上\(Splay\)相比起其他平衡树做起一些奇怪的操作要方便的多,反正干什么你都直接\(Splay\)就是了
\(Insert\)操作
插入一个权值为x的点,保证没有重复
void Insert(int x){
int u=rt;
if(!u) {
rt=++cnt,val[rt]=x;
return;
}
while(son[u][x>val[u]]) u=son[u][x>val[u]];
son[u][x>val[u]]=++cnt,val[cnt]=x;
Splay(cnt,0);
}
注意最后的\(Splay\)操作保证了复杂度
Find_Next操作
插叙一个节点\(x\)的前驱和后继
int Find_Next(int x,int d){
Splay(x,0);
int u=son[x][d];
if(!u) return -1;//不存在
while(son[u][!d]) u=son[u][!d];
Splay(u,0);//很关键
return u;
}
\(Delete\)操作
将节点编号为\(x\)的点删除
void Del(int x){
Splay(x,0);
if(!son[x][0]) {
rt=son[x][1];
fa[rt]=0;
return;
}//如果没有前驱,直接删除
int u=son[x][0];
while(son[u][1]) u=son[u][1];//找到x的前驱
//将前驱Splay到x后,前驱一定是左子树中最大的,它没有右儿子,所以直接将右儿子接上去就可以了
Splay(u,x);
son[u][1]=son[x][1];
fa[son[x][1]]=u;
rt=u;
}
如果觉得我的代码有问题,请尽快联系我
\(Splay\)使用的一些注意事项
1.\(Splay\)的本质依然只是一个\(BST\),所以\(BST\)能干的事它都能干
2.\(Splay\)常数大概是11倍左右,但是跑不满(\(LCT\)是跑满的...)
3.\(Splay\)不建议与其他数据结构嵌套
4.100000以上的数据使用\(Splay\)要小心
5.\(Splay\)操作的不同实现可能对常数有着很大影响
学了一些基本操作,我们搞搞模板题
T1 营业额统计
经典裸题,题意求\(a[1]+\sum _{i=2}^{i<=n} min_{j=1}^{j<i}\{ abs(a[i]-a[j]) \}\)
插入,求前驱和后继即可(我为什么不写set...)
注意学习一个新的数据结构时要有耐心,慢慢调...
#include<bits/stdc++.h>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(reg int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(reg int i=a,i##end=b;i>=i##end;--i)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=1e5+10,INF=1e9+10;
int n,m;
int rt,fa[N],son[N][2],sz[N],val[N],c[N],cnt;
void Up(int u){
sz[u]+=sz[son[u][0]]+sz[son[u][1]];
}
void rotate(int u){
int f=fa[u],ff=fa[fa[u]],d=son[f][0]==u?0:1,df=son[ff][0]==f?0:1;
son[ff][df]=u;
son[f][d]=son[u][!d];
fa[son[u][!d]]=f;
son[u][!d]=f;
fa[u]=ff,fa[f]=u;
Up(f),Up(u);
Up(ff);
}
void Splay(int u,int to){
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(fa[fa[u]]!=to) {
if((son[f][0]==u)^(son[ff][0]==f)) rotate(u);
else rotate(f);
}
rotate(u);
}
if(to==0) rt=u;
}
void Find(int x){
int u=rt;
while(son[u][x>val[u]]&&val[u]!=x) u=son[u][x>val[u]];
Splay(u,0);
}
//0 pre 1 nxt
int Find_Next(int x,int k){
Find(x);
if(val[rt]<=x&&!k) return val[rt];
if(val[rt]>=x&&k) return val[rt];
int v=son[rt][k];
if(!v) return INF;
while(son[v][!k]) v=son[v][!k];
return val[v];
}
void Insert(int x){
if(!rt) {
rt=++cnt;
son[cnt][0]=son[cnt][1]=0,c[cnt]=1,sz[cnt]=1;val[cnt]=x;
return;
}
Find(x);
if(val[rt]==x) {
c[rt]++;
return;
}
int u=rt;
while(son[u][x>val[u]]) u=son[u][x>val[u]];
son[u][x>val[u]]=++cnt;
fa[cnt]=u,son[cnt][0]=son[cnt][1]=0,c[cnt]=1,sz[cnt]=1;val[cnt]=x;
Splay(cnt,0);
}
int main(){
ll ans=0;
rep(i,1,n=rd()) {
int x=rd();
if(i==1) ans+=x;
else {
int pre=Find_Next(x,0);
int nxt=Find_Next(x,1);
ans+=min(abs(pre-x),abs(nxt-x));
}
Insert(x);
}
printf("%lld\n",ans);
}
T2 郁闷的出纳员
这题不需要区间操作
插入整体标记,第k大查询
查询第k大操作需要我们存储一个\(size\)值,\(cnt\)表示重复出现的次数
注意在\(Splay\)的时候要\(Up\)
第一次打第k大查询很有可能挂,注意每次\(while\)下去都必须\(Splay\)上来
这个删除操作比较奇怪,建议自己实现一下
void Up(int u){
if(!u) return;
sz[u]=sz[son[u][0]]+sz[son[u][1]];
}
#include<bits/stdc++.h>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(reg int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(reg int i=a,i##end=b;i>=i##end;--i)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=1e5+10,INF=2e9+10,P=1e9+7;
int n,lim,d;
int rt,fa[N],son[N][2],sz[N],val[N],c[N],cnt;
void Up(int u) {
if(!u) return;
sz[u]=c[u]+sz[son[u][0]]+sz[son[u][1]];
}
void rotate(int u){
int f=fa[u],ff=fa[f],d=(son[f][1]==u);
son[ff][son[ff][1]==f]=u;
son[f][d]=son[u][!d];
fa[son[u][!d]]=f;
son[u][!d]=f;
fa[f]=u;
fa[u]=ff;
Up(f),Up(u),Up(ff);
}
void Splay(int u,int to){
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(ff!=to) {
if((son[f][1]==u)^(son[ff][1]==f)) rotate(u);
else rotate(f);
}
rotate(u);
}
if(!to) rt=u;
}
void Insert(int x){
if(!rt) {
rt=++cnt;
son[cnt][0]=son[cnt][1]=0,c[cnt]=1,sz[cnt]=1;val[cnt]=x;
return;
}
int u=rt;
while(son[u][x>val[u]] && val[u]!=x) u=son[u][x>val[u]];
if(val[u]==x) {
c[u]++;
sz[u]++;
Splay(u,0);
return;
}
son[u][x>val[u]]=++cnt;
fa[cnt]=u,son[cnt][0]=son[cnt][1]=0,c[cnt]=1,sz[cnt]=1;val[cnt]=x;
Splay(cnt,0);
}
int ans;
void Del(){
int u=rt;
while(u){
if(son[u][0] && val[u]+d<=lim){
ans+=sz[son[u][0]];
son[u][0]=0;
}
if(val[u]+d<lim) {
ans+=c[u];
if(u==rt){
fa[son[u][1]]=0;
rt=son[u][1];
u=son[u][1];
continue;
} else {
fa[son[u][1]]=fa[u];
son[fa[u]][son[fa[u]][1]==u]=son[u][1];
if(!son[u][1]) {
if(fa[u]) Splay(fa[u],0);
break;
}
u=son[u][1];
continue;
}
}
if(son[u][0]) u=son[u][0];
else {
Splay(u,0);
break;
}
}
}
int Quekth(int k) {
if(sz[rt]<k) return -1;
int u=rt;
while(u) {
if(sz[son[u][1]]>=k) u=son[u][1];
else {
k-=sz[son[u][1]];
if(c[u]>=k) {
Splay(u,0);
return val[u]+d;
}
k-=c[u];
u=son[u][0];
}
}
return -1;
}
char opt[20];
int main(){
n=rd(),lim=rd();
rep(i,1,n) {
scanf("%s",opt);
int x=rd();
if(opt[0]=='I') {
if(x<lim) continue;
x-=d;
Insert(x);
} else if(opt[0]=='A') {
d+=x;
} else if(opt[0]=='S') {
d-=x;
} else if(opt[0]=='F') {
printf("%d\n",Quekth(x));
}
Del();
}
printf("%d\n",ans);
}
T3 宠物收养所
插入,查询前驱后继,删除操作
注意答案要取模
#include<bits/stdc++.h>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(reg int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(reg int i=a,i##end=b;i>=i##end;--i)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=1e5+10,INF=2e9+10,P=1e9+7;
int n,d;
int rt,fa[N],son[N][2],val[N],c[N],cnt;
void rotate(int u){
int f=fa[u],ff=fa[f],d=(son[f][1]==u);
son[ff][son[ff][1]==f]=u;
son[f][d]=son[u][!d];
fa[son[u][!d]]=f;
son[u][!d]=f;
fa[f]=u;
fa[u]=ff;
}
void Splay(int u,int to){
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(ff!=to) {
if((son[f][1]==u)^(son[ff][1]==f)) rotate(u);
else rotate(f);
}
rotate(u);
}
if(!to) rt=u;
}
void Insert(int x){
if(!rt) {
rt=++cnt;
son[cnt][0]=son[cnt][1]=0,c[cnt]=1;val[cnt]=x;
return;
}
int u=rt;
while(son[u][x>val[u]] && val[u]!=x) u=son[u][x>val[u]];
if(val[u]==x) {
c[u]++;
Splay(u,0);
return;
}
son[u][x>val[u]]=++cnt;
fa[cnt]=u,son[cnt][0]=son[cnt][1]=0,c[cnt]=1;val[cnt]=x;
Splay(cnt,0);
}
ll ans;
void Find(int x) {
int u=rt;
while(val[u]!=x && son[u][x>val[u]]) u=son[u][x>val[u]];
Splay(u,0);
}
int Find_Next(int x,int k){
Find(x);
if(val[rt]==x||((val[rt]<x)^k)) return rt;
int u=son[rt][k];
while(u && son[u][!k]) u=son[u][!k];
return u;
}
void Del(int x){
c[x]--;
if(c[x]) return;
int u=son[x][0],f=fa[x];
if(!u) {
fa[son[x][1]]=f;
son[f][son[f][1]==x]=son[x][1];
if(x==rt) rt=son[x][1];
return;
}
while(son[u][1]) u=son[u][1];
Splay(u,x);
son[u][1]=son[x][1];
fa[son[x][1]]=u;
fa[u]=f;
son[f][son[f][1]==x]=u;
if(x==rt) rt=u;
}
int main(){
n=rd();
rep(i,1,n) {
int k=rd(),x=rd();
if(!rt||k==d) {
Insert(x);
d=k;
continue;
}
int pre=Find_Next(x,0),nxt=Find_Next(x,1);
if(!pre || (nxt && val[nxt]-x<x-val[pre])) {
ans+=val[nxt]-x;
Del(nxt);
} else {
ans+=x-val[pre];
Del(pre);
}
}
printf("%lld\n",ans%1000000);
}
写到这里,我们对于\(Splay\)有了一些基础认识,可以来学习一些新的操作了
\(Splay\)区间更新,区间翻转
ll Addmark[N],sum[N];//区间加标记
void Down(int u){
if(!u) return;
Addmark[son[u][0]]+=Addmark[u];
Addmark[son[u][1]]+=Addmark[u];
sum[son[u][0]]+=sz[son[u][0]]*Addmark[u];
sum[son[u][1]]+=sz[son[u][1]]*Addmark[u];
}
我们先来学习经典的\(Down\)操作。。
\(Splay\)上的\(Down\)要稍微注意一下,有两种情况是必须要\(Down\)下去的
1.父子关系发生改变时(即\(rotate\)时)
2.查询节点权值时
再算上\(Up\)操作,我的\(Splay\)函数会变成这样
void rotate(int u) {
int f=fa[u],ff=fa[f],d=(son[f][1]==u),df=(son[ff][1]==f);
Down(ff),Down(f),Down(u);
son[ff][df]=u,fa[u]=ff;
son[f][d]=son[u][!d]; if(son[u][!d]) fa[son[u][!d]]=f;
son[u][!d]=f,fa[f]=u;
Up(f),Up(u),Up(ff);
}
void Splay(int u,int to){
Down(u);
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if((son[f][1]==u)^(son[ff][1]==f)) rotate(u);
else rotate(f);
}
if(!to) rt=u;
}
(但是经过严谨推导后,其实我们可以发现一些\(Up\)和\(Down\)是没有必要的,但是我们先打暴力嘛)
关于如何区间修改
将\(l-1 \ Splay\)到根,再将\(r+1 \ Splay\)到根下面,这样的话,我们要求的区间就会汇集在子树\(son[son[rt][1]][0]\)上
对于边界问题,当然可以打特判,不过建立两个哨兵会方便一些
void Upd(int l,int r,int x){
if(l==1&&r==n) {
sum[rt]+=1ll*x*sz[rt];
t[rt]+=x;
val[rt]+=x;
return;
}
if(l>1) Splay(l-1,0);
if(r<n) {
Splay(r+1,l-1);
sum[son[r+1][0]]+=x*sz[son[r+1][0]];
val[son[r+1][0]]+=x;
t[son[r+1][0]]+=x;
Splay(son[r+1][0],0);
return;
}
sum[son[rt][1]]+=sz[son[rt][1]];
t[son[rt][1]]+=x;
val[son[rt][1]]+=x;
Splay(son[rt][1],0);
}
这个是打了特判的版本
翻转操作也类似,就不再赘述了
来我们做一道\(Splay\)(线段树)裸题
T4 A Simple Problem with Integers
由于这份代码是我第一次打的(太傻帽了),不建议参考,对拍还是可以的
#include<cstdio>
#include<algorithm>
#include<cctype>
#include<iostream>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(reg int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(reg int i=a,i##end=b;i>=i##end;--i)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=1e5+10,INF=2e9+10,P=1e9+7;
int n,m;
int rt,fa[N],son[N][2],sz[N];
ll sum[N],val[N],t[N];
void Show(){
puts("Now Show The Tree");
cout<<"root="<<rt<<endl;
rep(i,1,n) {
if(son[i][0]) cout<<i<<' '<<son[i][0]<<endl;
if(son[i][1]) cout<<i<<' '<<son[i][1]<<endl;
}
rep(i,1,n) cout<<fa[i]<<' '<<val[i]<<' '<<sum[i]<<' '<<t[i]<<' '<<sz[i]<<endl;
}
void Up(int u){
if(!u) return;
sum[u]=val[u]+sum[son[u][1]]+sum[son[u][0]];
sz[u]=sz[son[u][0]]+sz[son[u][1]]+1;
}
void Down(int u){
if(!u||!t[u]) return;
t[son[u][0]]+=t[u];
t[son[u][1]]+=t[u];
sum[son[u][0]]+=t[u]*sz[son[u][0]];
sum[son[u][1]]+=t[u]*sz[son[u][1]];
val[son[u][0]]+=t[u];
val[son[u][1]]+=t[u];
t[u]=0;
}
void rotate(int u) {
int f=fa[u],ff=fa[f],d=(son[f][1]==u),df=(son[ff][1]==f);
son[ff][df]=u,fa[u]=ff;
son[f][d]=son[u][!d]; if(son[u][!d]) fa[son[u][!d]]=f;
son[u][!d]=f,fa[f]=u;
Up(f),Up(u),Up(ff);
}
void Splay(int u,int to){
if(!u) return;
Down(u);
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(ff!=to) {
if((son[f][1]==u)^(son[ff][1]==f)) rotate(f);
else rotate(u);
}
rotate(u);
}
if(!to) rt=u;
}
int Build(int l,int r){
if(l>r) return 0;
int u=(l+r)>>1;
fa[son[u][0]=Build(l,u-1)]=u;
fa[son[u][1]=Build(u+1,r)]=u;
Up(u);
return u;
}
char opt[10];
void DownNode(int rt,int x){
int u=rt;
while(u!=x) {
Down(u);
u=son[u][x>u];
}
}
ll Que(int l,int r){
if(l==1&&r==n) return sum[rt];
if(l>1) {
DownNode(rt,l-1);
Splay(l-1,0);
}
if(r<n) {
DownNode(rt,r+1),Splay(r+1,l-1);
return sum[son[r+1][0]];
}
return sum[son[rt][1]];
}
void Upd(int l,int r,int x){
if(l==1&&r==n) {
sum[rt]+=1ll*x*sz[rt];
t[rt]+=x;
val[rt]+=x;
return;
}
if(l>1) {
DownNode(rt,l-1);
Splay(l-1,0);
}
if(r<n) {
DownNode(rt,r+1),Splay(r+1,l-1);
sum[son[r+1][0]]+=x*sz[son[r+1][0]];
val[son[r+1][0]]+=x;
t[son[r+1][0]]+=x;
Splay(son[r+1][0],0);
return;
}
sum[son[rt][1]]+=sz[son[rt][1]];
t[son[rt][1]]+=x;
val[son[rt][1]]+=x;
Splay(son[rt][1],0);
}
int main(){
n=rd(),m=rd();
rep(i,1,n) val[i]=rd();
rt=Build(1,n);
rep(i,1,m) {
scanf("%s",opt);
int l=rd(),r=rd();
if(opt[0]=='Q') printf("%lld\n",Que(l,r));
else Upd(l,r,rd());
}
}
虽然打得很low但是还是能感觉到两种数据结构的速度差异。。。
其实写到后面也就是一些奇怪的操作的实现罢了,接下来我都是提供一种写法,仅供参考
T5 Robotic Sort
每次找到序列中最小的两个点,然后将一个较小的节点权值赋成无穷大(其实是将上一次完成排序的点删除),将两个点之间的区间翻转
#include<cstdio>
#include<algorithm>
#include<cctype>
#include<iostream>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(reg int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(reg int i=a,i##end=b;i>=i##end;--i)
#define dir(x) (son[fa[x]][1]==x)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=1e5+10,INF=2e9+10,P=1e9+7;
bool be;
int n,m;
int rt,fa[N],son[N][2];
int num[N],t[N];
struct Node{
int x,id;
bool operator < (const Node __) const{
return x<__.x||(id<__.id&&x==__.x);
}
bool operator == (const Node __) const{
return x==__.x&&id==__.id;
}
};
Node s[N],a[N];
int sz[N];
void Up(int u){
if(!u) return;
s[u]=a[u];
sz[u]=1;
if(son[u][0]) s[u]=min(s[u],s[son[u][0]]),sz[u]+=sz[son[u][0]];
if(son[u][1]) s[u]=min(s[u],s[son[u][1]]),sz[u]+=sz[son[u][1]];
}
void Down(int u){
if(!u||!t[u]) return;
t[son[u][0]]^=1,t[son[u][1]]^=1;
swap(son[u][0],son[u][1]);
t[u]=0;
}
void rotate(int u) {
int f=fa[u],ff=fa[f],d=dir(u);
if(ff) son[ff][dir(f)]=u;
fa[u]=ff;
son[f][d]=son[u][!d]; if(son[u][!d]) fa[son[u][!d]]=f;
son[u][!d]=f,fa[f]=u;
Up(f),Up(u),Up(ff);
}
void Splay(int u,int to){
if(!u) return;
Down(u);
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(ff!=to) {
if(dir(u)^dir(f)) rotate(f);
else rotate(u);
}
rotate(u);
}
if(!to) rt=u;
}
int Build(int l,int r){
if(l>r) return 0;
int u=(l+r)>>1;
t[u]=0;
fa[son[u][0]=Build(l,u-1)]=u;
fa[son[u][1]=Build(u+1,r)]=u;
Up(u);
return u;
}
int fir;
int Work(){
int u=rt,res=0,l;
if(fir) {
while(1) {
Down(u);
if(son[u][0] && s[son[u][0]]==s[u]) {
u=son[u][0];
continue;
}
if(a[u]==s[u]) break;
u=son[u][1];
}
s[u]=a[u]=(Node){(int)1e9,u};
Up(u);
Splay(u,0);
l=u;
} else fir=1,l=0;
u=rt;
while(1) {
Down(u);
if(son[u][0] && s[son[u][0]]==s[u]) {
u=son[u][0];
continue;
}
if(a[u]==s[u]) {
res+=sz[son[u][0]];
break;
}
res+=sz[son[u][0]]+1;
u=son[u][1];
}
Splay(u,0);
Down(u);
if(son[u][1]) {
u=son[u][1];
while(1) {
Down(u);
if(son[u][0]) u=son[u][0];
else break;
}
if(l) Splay(l,0);
Splay(u,l);
t[son[u][0]]^=1;
} else {
if(l) {
Splay(l,0);
t[son[rt][1]]^=1;
} else t[rt]^=1;
}
return res+1;
}
bool ed;
int main(){
while(~scanf("%d",&n) && n) {
rep(i,1,n) a[i]=(Node){rd(),i};
fa[rt=Build(1,n)]=0;
fa[0]=0,sz[0]=0;
s[0]=(Node){(int)1e9,0};
fir=0;
rep(i,1,n-1) printf("%d ",Work());
printf("%d\n",n);
}
}
T6 Queue-jumpers
这题涉及到了多种\(Splay\)经典操作
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=2e5+10;
#define dir(x) (son[fa[x]][1]==x)
int n,m,rt;
int h[N],cnt,c;
int L[N],R[N];
int fa[N],son[N][2],sz[N];
void Show(){
rep(i,1,c) {
if(son[i][0]) cout<<i<<' '<<son[i][0]<<" 0"<<endl;
if(son[i][1]) cout<<i<<' '<<son[i][1]<<" 1"<<endl;
}
rep(i,1,c) cout<<fa[i]<<' '<<sz[i]<<endl;
}
void Up(int u) {
if(!u) return;
sz[u]=R[u]-L[u]+1;
if(son[u][0]) sz[u]+=sz[son[u][0]];
if(son[u][1]) sz[u]+=sz[son[u][1]];
}
void rotate(int u) {
int f=fa[u],ff=fa[f],d=dir(u);
if(ff) son[ff][dir(f)]=u; fa[u]=ff;
son[f][d]=son[u][!d]; if(son[u][!d]) fa[son[u][!d]]=f;
son[u][!d]=f,fa[f]=u;
Up(f),Up(u),Up(ff);
}
void Splay(int u,int to){
if(!u) return;
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(ff!=to) {
if(dir(u)^dir(f)) rotate(u);
else rotate(f);
}
rotate(u);
}
if(!to) rt=u;
}
int Build(int l,int r){
if(l>r) return 0;
int u=(l+r)>>1;
fa[son[u][0]=Build(l,u-1)]=u;
fa[son[u][1]=Build(u+1,r)]=u;
Up(u);
return u;
}
int opt[N],optx[N],id[N];
char option[10];
void Top(int x){
Splay(x,0);
if(!son[x][0]) return;
if(!son[x][1]){
swap(son[x][0],son[x][1]);
return;
} else {
int u=son[x][1];
while(son[u][0]) u=son[u][0];
Splay(u,x);
fa[son[x][0]]=son[x][1];
son[son[x][1]][0]=son[x][0];
Up(son[x][1]);
son[x][0]=0;
}
}
int Que(int x){
Splay(x,0);
return sz[son[x][0]]+1;
}
int Rank(int x){
int u=rt;
while(u) {
if(sz[son[u][0]]>=x) {
u=son[u][0];
continue;
}
x-=sz[son[u][0]];
if(R[u]-L[u]+1>=x) {
Splay(u,0);
return L[u]+x-1;
}
x-=R[u]-L[u]+1;
u=son[u][1];
}
return -1;
}
int main(){
rep(kase,1,rd()) {
n=rd(),m=rd();
cnt=0;
rep(i,1,m) {
scanf("%s",option);
optx[i]=rd();
if(option[0]=='T') opt[i]=0,h[++cnt]=optx[i];
else if(option[0]=='Q') opt[i]=1,h[++cnt]=optx[i];
else opt[i]=2;
}
sort(h+1,h+cnt+1);
cnt=unique(h+1,h+cnt+1)-h-1;
int pre=0;
c=0;
rep(i,1,cnt) {
if(h[i]-1>pre) L[++c]=pre+1,R[c]=h[i]-1;
L[++c]=h[i],R[c]=h[i];
id[i]=c;
pre=h[i];
}
if(n>pre) L[++c]=pre+1,R[c]=n;
fa[rt=Build(1,c)]=0;fa[0]=sz[0]=0;
printf("Case %d:\n",kase);
rep(i,1,m) {
if(opt[i]==0) Top(id[lower_bound(h+1,h+cnt+1,optx[i])-h]);
else if(opt[i]==1) printf("%d\n",Que(id[lower_bound(h+1,h+cnt+1,optx[i])-h]));
else printf("%d\n",Rank(optx[i]));
}
}
}
T7 Play with Chain
对于移动链的操作,先把链断开,再找到对应插入位置,再插入
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=3e5+10;
#define dir(x) (son[fa[x]][1]==x)
int n,m,rt;
int fa[N],son[N][2],sz[N],t[N];
void Show(){
puts("Now Show The Splay Tree");
cout<<"rt="<<rt<<endl;
rep(i,1,n) {
if(son[i][0]) cout<<i<<' '<<son[i][0]<<" 0"<<endl;
if(son[i][1]) cout<<i<<' '<<son[i][1]<<" 1"<<endl;
}
rep(i,1,n) cout<<son[i][0]<<' '<<son[i][1]<<' '<<"t="<<t[i]<<' '<<"sz="<<sz[i]<<endl;
}
void Up(int u) {
if(!u) return;
sz[u]=1;
if(son[u][0]) sz[u]+=sz[son[u][0]];
if(son[u][1]) sz[u]+=sz[son[u][1]];
}
void Down(int u){
if(!u||!t[u]) return;
swap(son[u][0],son[u][1]);
t[son[u][0]]^=1;
t[son[u][1]]^=1;
t[u]=0;
}
void rotate(int u){
int f=fa[u],ff=fa[f],d=dir(u);
fa[u]=ff; if(ff) son[ff][dir(f)]=u;
son[f][d]=son[u][!d]; if(son[u][!d]) fa[son[u][!d]]=f;
fa[son[u][!d]=f]=u;
Up(f),Up(u),Up(ff);
}
void Splay(int u,int to){
if(!u) return;
Down(u);
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(ff!=to) {
if(dir(u)^dir(f)) rotate(u);
else rotate(f);
}
rotate(u);
}
if(!to) rt=u;
}
int Find(int x){
int u=rt;
while(1) {
Down(u);
if(sz[son[u][0]]>=x) {
u=son[u][0];
continue;
}
x-=sz[son[u][0]];
if(x==1) break;
x--;
u=son[u][1];
}
return u;
}
void Move(int l,int r,int c){
if(l==1&&r==n) return;
if(l==1) l=0;
else {
l--;
l=Find(l);
Splay(l,0);
}
int tmp;
if(r==n) {
tmp=son[rt][1];
son[rt][1]=0;
Up(rt);
} else {
r++;
r=Find(r);
Splay(r,l);
tmp=son[r][0];
son[r][0]=0;
Up(r),Up(rt);
}
if(c==0) {
Splay(Find(1),0);
fa[son[rt][0]=tmp]=rt;
Up(rt);
return;
}
Splay(Find(c),0);
if(son[rt][1]) {
int u;
Splay(u=Find(c+1),rt);
son[u][0]=tmp;
fa[tmp]=u;
Up(u);
Up(rt);
} else {
son[rt][1]=tmp;
fa[tmp]=rt;
Up(rt);
}
}
void Rev(int l,int r){
if(l==1&&r==n) {
t[rt]^=1;
return;
}
if(l==1) l=0;
else {
l--;
l=Find(l);
Splay(l,0);
}
if(r==n) t[son[rt][1]]^=1;
else {
r++;
r=Find(r);
Splay(r,l);
t[son[r][0]]^=1;
}
}
int printcnt;
void Getline(int x){
Down(x);
if(son[x][0]) Getline(son[x][0]);
printf("%d%c",x,++printcnt==n?'\n':' ');
if(son[x][1]) Getline(son[x][1]);
}
int Build(int l,int r){
if(l>r) return 0;
int u=(l+r)>>1;
t[u]=0;
fa[son[u][0]=Build(l,u-1)]=u;
fa[son[u][1]=Build(u+1,r)]=u;
Up(u);
return u;
}
char opt[10];
int main(){
while(~scanf("%d%d",&n,&m) && ~n ) {
fa[rt=Build(1,n)]=0;
fa[0]=sz[0]=0;
rep(i,1,m) {
scanf("%s",opt);
if(opt[0]=='C') {
int a=rd(),b=rd(),c=rd();
Move(a,b,c);
} else {
int l=rd(),r=rd();
Rev(l,r);
}
}
printcnt=0;
Getline(rt);
}
}
T8 文本编辑器editor0
没错一百万的数据
不过这题数据好像有锅
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=1<<21;
#define dir(x) (son[fa[x]][1]==x)
int n,rt;
int fa[N],son[N][2],sz[N],t[N];
char s[N],val[N];
void Up(int u) {
if(!u) return;
sz[u]=1;
if(son[u][0]) sz[u]+=sz[son[u][0]];
if(son[u][1]) sz[u]+=sz[son[u][1]];
}
void Down(int u){
if(!u||!t[u]) return;
swap(son[u][0],son[u][1]);
t[son[u][0]]^=1;
t[son[u][1]]^=1;
t[u]=0;
}
void Getline(int x){
Down(x);
if(son[x][0]) Getline(son[x][0]);
putchar(val[x]);
if(son[x][1]) Getline(son[x][1]);
}
void Show(){
puts("Now Show The Splay Tree");
rep(i,1,n) {
if(son[i][0]) cout<<i<<' '<<son[i][0]<<" 0"<<endl;
if(son[i][1]) cout<<i<<' '<<son[i][1]<<" 1"<<endl;
}
rep(i,1,n) cout<<fa[i]<<' '<<sz[i]<<' '<<t[i]<<' '<<val[i]<<endl;
}
void rotate(int u){
int f=fa[u],ff=fa[f],d=dir(u);
Down(ff),Down(f),Down(u);
fa[u]=ff; if(ff) son[ff][dir(f)]=u;
son[f][d]=son[u][!d]; if(son[u][!d]) fa[son[u][!d]]=f;
fa[son[u][!d]=f]=u;
Up(f),Up(u),Up(ff);
}
void Splay(int u,int to){
if(!u) return;
Down(u);
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(ff!=to) {
if(dir(u)^dir(f)) rotate(u);
else rotate(f);
}
rotate(u);
}
if(!to) rt=u;
}
char opt[10];
int Build(int l,int r){
if(l>r) return 0;
int u=++n,mid=(l+r)>>1;
val[u]=s[mid];
fa[son[u][0]=Build(l,mid-1)]=u;
fa[son[u][1]=Build(mid+1,r)]=u;
Up(u);
return u;
}
int Find(int x){
int u=rt;
while(1) {
Down(u);
if(sz[son[u][0]]>=x) {
u=son[u][0];
continue;
}
x-=sz[son[u][0]];
if(x==1) break;
x--;
u=son[u][1];
}
return u;
}
int Next(int x,int d){
Splay(x,0);
Down(x);
x=son[x][d];
Down(x);
while(son[x][!d]){
x=son[x][!d];
Down(x);
}
return x;
}
int now;
int main(){
rd();
now=rt=n=1;
while(~scanf("%s",opt)) {
if(opt[0]=='I') {
int c=0,l=rd();
rep(i,1,l) s[++c]=getchar();
int t=Build(1,c);
int nxt=Next(now,1);
if(nxt) {
Splay(nxt,0);
Splay(now,rt);
}
fa[son[now][1]=t]=now;
Up(now),Up(rt);
} else if(opt[0]=='M') now=Find(rd()+1);
else if(opt[0]=='G') {
int nxt=Next(now,1);
putchar(val[nxt]);
if(val[nxt]!='\n') puts("");
} else if(opt[0]=='N') now=Next(now,1);
else if(opt[0]=='P') now=Next(now,0);
else if(opt[0]=='D') {
Splay(now,0);
int l=rd();
if(sz[son[now][1]]==l) {
son[now][1]=0;
Up(now);
continue;
}
int t=Find(sz[son[now][0]]+l+2);
Splay(t,now);
son[t][0]=0;
Up(t),Up(now);
} else {
Splay(now,0);
int l=rd();
if(sz[son[now][1]]==l) {
t[son[now][1]]^=1;
continue;
}
int t=Find(sz[son[now][0]]+l+2);
Splay(t,now);
::t[son[t][0]]^=1;
}
}
}
T9 维修数列
不多说了,注意代码常数,如果你写T了,可以看一下我的实现
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#include<cassert>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=5e5+10,INF=1e9+10;
#define dir(x) (son[fa[x]][1]==x)
int m,rt;
int fa[N],son[N][2];
int Setmark[N],Revmark[N];
int stk[N],top;
struct Node{
ll ls,rs,s,ma;
int sz;
Node operator + (const Node x) const {
Node res;
res.ls=max(ls,s+x.ls);
res.rs=max(x.rs,x.s+rs);
res.s=s+x.s;
res.ma=max(max(ma,x.ma),rs+x.ls);
res.sz=sz+x.sz;
return res;
}
void operator = (const int x) {
s=sz*x;
ls=rs=ma=max(x,sz*x);
}
}s[N],val[N];
void Up(int u){
if(!u) return;
if(son[u][0]) s[u]=s[son[u][0]]+val[u];
else s[u]=val[u];
if(son[u][1]) s[u]=s[u]+s[son[u][1]];
}
void Down(int u){
if(!u) return;
if(Setmark[u]!=INF) {
if(son[u][0]) {
Setmark[son[u][0]]=Setmark[u];
Revmark[son[u][0]]=0;
s[son[u][0]]=Setmark[u];
val[son[u][0]]=Setmark[u];
}
if(son[u][1]) {
Setmark[son[u][1]]=Setmark[u];
Revmark[son[u][0]]=0;
s[son[u][1]]=Setmark[u];
val[son[u][1]]=Setmark[u];
}
Setmark[u]=INF;
}
if(Revmark[u]) {
if(son[u][0]) {
Revmark[son[u][0]]^=1;
swap(s[son[u][0]].ls,s[son[u][0]].rs);
}
if(son[u][1]) {
Revmark[son[u][1]]^=1;
swap(s[son[u][1]].ls,s[son[u][1]].rs);
}
swap(son[u][0],son[u][1]);
Up(u);
Revmark[u]=0;
}
}
void rotate(int u){
int f=fa[u],ff=fa[f],d=dir(u);
Down(ff),Down(f),Down(u);
fa[u]=ff; if(ff) son[ff][dir(f)]=u;
son[f][d]=son[u][!d]; if(son[u][!d]) fa[son[u][!d]]=f;
fa[f]=u,son[u][!d]=f;
Up(f),Up(u),Up(ff);
}
void Splay(int u,int to){
Down(u);
while(fa[u]!=to) {
int f=fa[u],ff=fa[f];
if(ff!=to) {
if(dir(u)^dir(f)) rotate(u);
else rotate(f);
}
rotate(u);
}
if(!to) rt=u;
}
int a[N],tot;
int Build(int l,int r){
if(l>r) return 0;
int mid=(l+r)>>1,u=stk[top--];
val[u].sz=1;val[u]=a[mid];
Setmark[u]=INF;Revmark[u]=0;
fa[son[u][0]=Build(l,mid-1)]=u;
fa[son[u][1]=Build(mid+1,r)]=u;
Up(u);
return u;
}
int Find(int x){
int u=rt;
while(1) {
Down(u);
if(s[son[u][0]].sz>=x) { u=son[u][0]; continue; }
if((x-=s[son[u][0]].sz)==1) break;
x--,u=son[u][1];
}
return u;
}
void Insert(int p){
p++;
Splay(Find(p),0);
Splay(Find(p+1),rt);
fa[son[son[rt][1]][0]=Build(1,tot)]=son[rt][1];
Up(son[rt][1]),Up(rt);
}
queue <int> que;
void Del(int l,int r){
r+=2;
Splay(Find(l),0);
Splay(Find(r),rt);
que.push(son[son[rt][1]][0]);
while(!que.empty()) {
int u=que.front(); que.pop();
stk[++top]=u;
if(son[u][0]) que.push(son[u][0]);
if(son[u][1]) que.push(son[u][1]);
}
son[son[rt][1]][0]=0;
Up(son[rt][1]),Up(rt);
}
void Set(int l,int r,int x){
r+=2;
Splay(Find(l),0);
Splay(Find(r),rt);
int t=son[son[rt][1]][0];
Revmark[t]=0,Setmark[t]=x;
s[t]=x,val[t]=x;
Up(son[rt][1]),Up(rt);
}
void Reverse(int l,int r){
r+=2;
Splay(Find(l),0);
Splay(Find(r),rt);
int t=son[son[rt][1]][0];
if(Setmark[t]!=INF) return;
Revmark[t]^=1;
swap(s[t].ls,s[t].rs);
Up(son[rt][1]),Up(rt);
}
ll GetSum(int l,int r){
r+=2;
Splay(Find(l),0);
Splay(Find(r),rt);
return s[son[son[rt][1]][0]].s;
}
ll GetAns(){
return s[rt].ma;
}
char opt[20];
int main(){
tot=rd(),m=rd();
drep(i,N-1,1) stk[++top]=i;
tot+=2;
rep(i,2,tot-1) a[i]=rd();
a[tot]=a[1]=-INF;
fa[rt=Build(1,tot)]=0;
rep(tttt,1,m) {
scanf("%s",opt);
if(opt[0]=='I') {
int p=rd();
rep(i,1,tot=rd()) a[i]=rd();
Insert(p);
} else if(opt[0]=='D') {
int l=rd(),r=rd()+l-1;
Del(l,r);
} else if(opt[0]=='M'&&opt[2]=='K') {
int l=rd(),r=rd()+l-1;
Set(l,r,rd());
} else if(opt[0]=='R') {
int l=rd(),r=rd()+l-1;
Reverse(l,r);
} else if(opt[0]=='G') {
int l=rd(),r=rd()+l-1;
printf("%lld\n",GetSum(l,r));
} else printf("%lld\n",GetAns());
}
}
T10 Box
毕竟是压轴的题,还是有一定思维难度的
(其实就是一个LCT裸题嘛)
做法是,将每棵树化成括号序列,建立\(Splay\)森林
一个子树就是一段区间,然后就可以直接整个区间移动了
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#include<cassert>
#include<cstring>
using namespace std;
#define reg register
typedef long long ll;
#define rep(i,a,b) for(reg int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(reg int i=a,i##end=b;i>=i##end;--i)
char IO;
int rd(){
int s=0,f=0;
while(!isdigit(IO=getchar())) if(IO=='-') f=1;
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return f?-s:s;
}
const int N=1e5+10,INF=1e9+10;
#define dir(x) (son[fa[x]][1]==x)
bool be;
int n,m;
int fa[N],son[N][2];
struct Edge{
int to,nxt;
}e[N<<1];
int head[N],ecnt,ind[N];
void AddEdge(int u,int v){
e[++ecnt]=(Edge){v,head[u]};
head[u]=ecnt;
ind[v]++;
}
int line[N],lc;
void dfs(int u){
line[++lc]=u;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].to;
dfs(v);
}
line[++lc]=u+n;
}
void rotate(int u){
int f=fa[u],ff=fa[f],d=dir(u);
fa[u]=ff; if(ff) son[ff][dir(f)]=u;
son[f][d]=son[u][!d]; if(son[u][!d]) fa[son[u][!d]]=f;
son[u][!d]=f,fa[f]=u;
}
void Splay(int u,int to){
while(fa[u]!=to && fa[u]) {
int f=fa[u],ff=fa[f];
if(ff!=to) {
if(dir(f)^dir(u)) rotate(u);
else rotate(f);
}
rotate(u);
}
}
int Build(int l,int r){
if(l>r) return 0;
int mid=(l+r)>>1,u=line[mid];
fa[son[u][0]=Build(l,mid-1)]=u;
fa[son[u][1]=Build(mid+1,r)]=u;
return u;
}
int GetRoot(int x){
Splay(x,0);
while(son[x][0]) x=son[x][0];
Splay(x,0);
return x;
}
void Move(int x,int to){
Splay(x,0);
if(son[x][0]) {
int l=son[x][0];
while(son[l][1]) l=son[l][1];
Splay(l,0);
Splay(x+n,l);
int r=x+n;
r=son[r][1];
while(son[r][0]) r=son[r][0];
Splay(r,l);
if(!to) {
fa[son[r][0]]=0;
son[r][0]=0;
return ;
}
x=son[r][0],son[r][0]=0;
fa[x]=0;
Splay(to,0);
if(fa[x]) {
Splay(x,0);
son[r][0]=x;fa[x]=r;
return;
}
int t=son[to][1];
while(son[t][0]) t=son[t][0];
Splay(t,to);
son[t][0]=x;
fa[x]=t;
} else {// A whole tree
if(!to) return;
Splay(to,0);
if(fa[x]) return;
int t=son[to][1];
while(son[t][0]) t=son[t][0];
Splay(t,to);
son[t][0]=x;
fa[x]=t;
}
}
bool ed;
int fir;
char opt[10];
int main(){
//cout<<&ed-&be<<endl;
while(~scanf("%d",&n)) {
if(fir) puts("");
else fir=1;
memset(ind,0,sizeof ind);memset(head,0,sizeof head),ecnt=0;
lc=0;
rep(i,1,n) {
int x=rd();
if(x) AddEdge(x,i);
}
rep(i,1,n) if(!ind[i]) {
int t=lc+1;
dfs(i);
fa[Build(t,lc)]=0;
}
fa[0]=0;
rep(i,1,m=rd()) {
scanf("%s",opt);
if(opt[0]=='Q') printf("%d\n",GetRoot(rd()));
else {
int x=rd(),to=rd();
if(x^to) Move(x,to);
}
}
}
}



