「C++」简单递推：你以为它很简单，其实它并不难

这是一个公式：

\[a_{i-1} + a_{i-4} = a_{i} \]

这个公式初看没有什么特别的，但是再看，就可以发现这是一个递推公式，通过这个公式，我们可以简单的写出求第n项的代码：

#include<bits/stdc++.h>
using namespace std;
long long a[110];
int main() {
    a[1] = 1, a[2] = 2, a[3] = 3, a[4] = 4, a[5] = 5; // 为了递推初始化前面5项
    for(int i = 6; i <= 100; ++ i) {
        a[i] = a[i - 1] + a[i - 4];   
    }
    while(true) {
        int n;
        cin >> n;
        if(n == 0) break;
        else cout << a[n] << "\n";
    }
    return 0;
}

注意，这个代码是求n小于等于100时的情况，n在这个情况下如果很大就会爆int，所以我们的数组要定义成long long。

根据公式来推，这不就是纯纯的小模拟吗？但是如果给它伪装到一个题目里面去，你还能发现这个公式吗？

Q1：繁衍

题目背景

正所谓一生二，二生三，三生万物，你作为造物主创造了一种全新的物种，这种生物为胎生动物，一年生一只，新生的从第五个年头开始，每年年初也生一只。请问第N年该生物数量。

输入格式

多组输入，每组输入占一行，一行一个数字N表示第N年（0<N<=100)，当N=0时表示输入结束不做处理。

输出格式

对于每组数据输出第N年该生物数量，每组输出占一行。

输入输出样例

输入 #1

1
2
3
4
5
6
0

输出 #1

1
2
3
4
5
7

提示

第一年就一个第一年刚被创造没生，第二年生了一个，第三年也生了一个以次类推，一直到第6年，第二年出生的那个已经长了4年第六年是他出生第五年所以生了一个加起来第六年是7个。

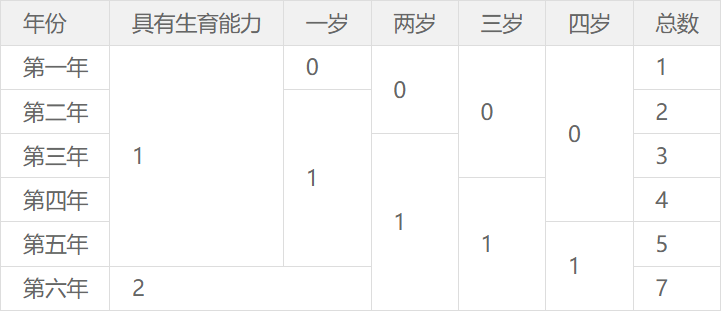
分析

现在就可以告诉你了，这一道题的代码就是上面的代码，公式也是上面的公式，可是问题来了，为什么这道题用的是上面的公式呢？This is a good problem.

表格上面已经给出了a[1]到a[5]的值（a[0]舍弃的情况下），我们可以根据题目的描述和已经给出的条件来推理。

首先，我们已知每一个胎生动物长到5岁时就开始无限生娃（具体无不无限咱也不知道），这里a[i-1]就是去年这种动物的数量，而a[i-4]就是五年前，也就是第i年可以繁殖的生物的数量，将他们相加起来就是简单这种生物第i年的数量。

代码略。

我们来看看下面一道题：

Q2：三步问题

题目描述

小明正在上楼梯，楼梯有n阶台阶，小达一次可以上1阶、2阶或3阶。请你计算小达有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。

输入格式

输入一个正整数n（≤1e6），代表台阶数

输出格式

输出一个整数，为方案数模1000000007的结果

输入输出样例

输入 #1

3

输出 #1

4

输入 #2

5

输出 #2

13

分析

这道题其实是一道斐波那契数列的变式，我们假设目前有6级楼梯，很轻松就能把每一个楼层的方案数量列举出来，也就是：

\[1, 2, 4, 7, 13, 24 \]

根据这个数列，我们可以知道这道题目的递推公式：

\[a_{n-3} + a_{n-2} + a_{n-1} = a_n \]

再根据这个递推公式，我们就可以写出代码（其实做递推的题目最简单的就是如上的步骤，这样就可以很快写出代码）

代码

#include<bits/stdc++.h>
using namespace std;  
const long long MOD = 1000000007; //别忘了取模
class Solution {  
public:  
    long long waysToStep(int n) {
        vector<long long> dp(n + 1, 0);
        dp[0] = 1; 
        for(long long i = 1; i <= n; i++) {
            for(long long j = 1; j <= 3 && i - j >= 0; j++) {
                dp[i] += dp[i - j] % MOD;
            }
        }
    return dp[n];
    }
};
  
int main() {  
    Solution solution;  
    long long n;
    cin >> n;
    long long ans = solution.waysToStep(n);  
    cout << ans % MOD;  
    return 0;  
}

（总感觉这个代码写的复杂了）

OK，这篇博客很短，因为递推这个东西，简单的时候你以为它很简单，其实它并不难。