数论补全计划【蒟蒻数论乱证】& 一些小清新算法

写在前面

\[ \Huge \color {aqua} {Updating！！！} \]

55然而我太逊了所以虎哥讲数论的时候一直把数论的费马小定理什么都都咕着，导致我现在学组合数取模啥都不会，所以就有了这个计划

虎哥写的blog比我写的好多了，而且贼全，我就自己重复证一证加深印象⑧

虎哥的blog✌

奇怪怪我不会LATEX。。。那我就这么着打吧

我就瞎整了奥

\(\text{Update 2022.7.22}\)：会 \(\LaTeX\) 了。。

\(\text{Update 2022.10.13}\)：由于转了 \(\text{markdown}\) 所以页面整个的崩掉了，现已修复 \(\text{markdown}\)，顺便修了一下 \(\LaTeX\)。

---

\(逆元\)

当 \(\gcd(a,b) == 1\) 即 \(a\) 与 \(b\) 互质时，存在乘法逆元：

\[a \times x ≡ 1 \pmod b \]

逆元得先存在奥！\(a\) 和 \(b\) 互质时才有逆元！

---

\(证明\)：

\(\frac{a}{b} \bmod p ≠ \frac{a \bmod p}{b \bmod p} \bmod p\)，这个让人觉得很烦，有一天就有数学家想解决这个问题。

当 \(\frac{a}{b} \bmod p = m\)

假设存在 \((a \times x) \bmod p = m\)

对于第一个柿子，在两边都乘上一个 \(b\)：

\[a \bmod p = ( m \times (b \bmod p) ) \bmod p \]

如果\(a<p\) && \(b<p\)，那就有：

\[a = (m \times b) \bmod p \]

然后再在两边乘上 \(x\)：

\[(a \times x) \bmod p = (m \times b \times x) \bmod p \]

然后一看，这左边的柿子真真的熟悉，然后看最开始咱假设那个，然后就发现了神奇的东西：

\[m = m \times b \times x \bmod p \]

\[a \times x \bmod p = m = m \times b \times x \bmod p \]

把两边的 \(m\) 一消:

\[(b \times x) \bmod p = 1 \]

就称 \(x\) 是 \(b\) 在 \(\bmod\ p\) 意义下滴逆元，\(x\) 记作 \(b^{-1}\)。

“证毕”。

---

嗐 所以咱就看到，想求 \(\frac{a}{b} \bmod p\) 也就是求 \(a \times x \bmod p\)。

然后咋求逆元的话。。。我把虎哥的线性求逆元代码粘过来吧(

%%%虎哥的证明%%%：

虎哥的代码

// 因为 1<i<p，所以 p/i 一定小于 p
ny[1] = 1;
for (int i = 2; i < p; ++i) {
    ny[i] = (long long)(p - p / i) * ny[p % i] % p; // 注意最后的模 p 不要忘记
}

然后我顺便解释一下虎哥证明中那个『\(i \times i^{-1} = 1\)』。(在证明里边乘 \(1\) 不变所以虎哥消了)

---

咱知道那逆元的定义是 \(x\) 是 \(a\) 在 \(\bmod\ p\) 意义下的逆元，记作 \(a^{-1}\)。

那就有：

\[a \times x ≡ 1 \pmod p \]

\[a \times x \bmod p = 1 \]

即$$a \times a^{-1} \bmod p = 1$$

在虎哥的证明里，\(i\) 和 \(r\) 都小于模数 \(p\)，所以：

\[a \times a^{-1}= 1 \]

“证毕”

---

但是我看好多别的相乘并不是 \(1\)，我一个蒟蒻也不明白为什么...

\(Update\)：因为没有取模((

---

刚才说了线性求逆元，这里说一下如何在 \(\mathcal{O(logn})\) 求单个数的逆元。

求逆元的最常用方法是费马小定理求逆元，很好记。但是缺陷是必须保证模数是个质数。

就比如说要求 \(x\) 的在 \(\bmod\ p\) 意义下的逆元，那么就直接求 \(x^{p-2}\) 就好了。

套个快速幂即可。

费马小定理求逆元

#define mod %
#define P ...// 某个质数

long long x;

inline long long ksm(long long A, long long B){
    long long res(1);
    while (B != 0){
        if ((B & 1) == 1) res = res * A mod P;
        A = A * A mod P;
        B >>= 1;
    }
    return res;
}

signed main(){
    cin >> x;
    cout << "x的逆元为：" << ksm(x, P-2) << '\n';
    return 0;
}

---

拓展一下，线性求阶乘逆元，这玩意在组合数那一块挺常用的。(\(p\) 得是质数奥)(逆元得存在奥)

线性求阶乘逆元

#define mod %
#define P ...// 某个质数

long long jc[N], ny[N];// 阶乘、逆元

inline long long ksm(long long A, long long B){
    long long res(1);
    while (B != 0){
        if ((B & 1) == 1) res = res * A mod P;
        A = A * A mod P;
        B >>= 1;
    }
    return res;
}

signed main(){
    jc[0] = 1;
    for (long long i = 1 ; i <= n ; ++ i)
        jc[i] = jc[i-1] * i mod P;
    
    ny[n] = ksm(jc[n], P-2);
    for (long long i = n-1 ; i >= 1 ; -- i)
        ny[i] = ny[i+1] * (i+1) mod P;
    
    // 此时ny[i]即为i!的逆元了

    return 0;
}

考虑一下为啥这样求是对的。可以感性理解一下，认为 \(x^{-1} = \frac{1}{x}\)，那么阶乘逆元就可以这样表示：

\[\frac{1}{x!} = \frac{1}{(x+1)!} \times (x+1) \]

那么也就是\((x!)^{-1} = ((x+1)!)^{-1} * (x+1)\) 了。

---

如果说要求 \(p\) 为合数的情况下 \(x\) 的逆元，其实也不难，用拓展欧几里得算法可以求出来。

---

\(欧拉函数\)

欧拉函数就是从 \(1\) 到 \(n\) 中与 \(n\) 互质的数，有的资料说是 \(1\) 到 \(n-1\) 的，我觉得应该是 \(n\) 与 \(n-1\) 肯定互质吧 \((n ≠ 2)\)?

\(φ(n) = n \times \frac{p_i - 1}{p_i}\)，其中 \(p_i\) 是 \(n\) 的质因数。

这个通项公式完全不会证阿 先记住咕着。。

\(Update\)：然而蒟蒻看了李煜东的蓝书后又会证了，来补一下。

---

设 \(p、q\) 为 \(n\) 的两个质因子。

那么根据 \(p\) 和 \(q\) 能筛出来的与 \(n\) 不互质的数就有 \(\frac{n}{p}+\frac{n}{q}\) 个，那么暂时确定的与 \(n\) 互质的数就有 \(n - \frac{n}{p} - \frac{n}{q}\) 个。

但是对于 \(p \times q\) 这个因子而言相当于他删了两次（要实在理解不了就举 \(n\) 为 \(12\) 手模一下），所以要加回来一次。

所以目前根据 \(p、q\) 确定的 \(1\) 到 \(n\) 中与 \(n\) 互质的数有 \(n - \frac{n}{p} - \frac{n}{q} + \frac{n}{p \times q}\) 个。

然后再推广到 \(n\) 的所有质因子就是上面写的那个公式了。

---

李煜东那本书上证明的挺好的，不过我学不来所以如果我写的实在看不懂就去看李煜东那本书上的吧，简单易懂。。

然后我又把虎哥的性质和证明粘过来力 不过我自己在草纸上证了，但实在懒得打...

\(求欧拉函数\)

这里虎哥给了两个情况，一个是求 \(1 \sim n\) 的，一个是单求 \(n\) 的

两种情况の代码

#include <bits/stdc++.h>
#define N 1000005
using namespace std;
int getphi(int n) {//单独求n的 
	int SQ = int(sqrt(n + 0.5)), ans = n;
	//如果有大于根号n的质因子那只能有一个，这种情况最后特判 
	//举例：99，sqrt(99)约等于10，但是他有一个大于10滴质因子11
	for (int i = 2 ; i <= SQ ; ++ i) {
		if (n % i == 0) {
			ans = (ans * (i-1)) / i;//欧拉函数通项公式
			while (n % i == 0)
				n /= i;//分解质因数 
		}
	}
	if (n >= 2) ans = (ans * (n-1)) / n;//n是那个 > sqrt(n)的质因子 
	return ans;
}
bool not_prime[N];
int phi[N], prime[N], tot;
void getqjphi(int n) {
	phi[1] = 1;
	for (int i = 2 ; i <= n ; ++ i) {
		if (not_prime[i] == false) {
			prime[++ tot] = i;
			phi[i] = i - 1;//性质2，i是质数，φ(p) = p-1 
		}
		for (int j = 1 ; j <= tot ; ++ j) {
			if (i * prime[j] > n)
				break;
			not_prime[i * prime[j]] = true;
			if (i % prime[j] == 0) {//变形1
				phi[i*prime[j]] = prime[j]*phi[i];
				break;
			}
			else //变形2
				phi[i*prime[j]] = (prime[j]-1) * phi[i];
		}
	}
}
void work() {
	
}
signed main() {
	work();
	return 0;
}

实际上只记第一个就可以，在考试的时候如果要求 \(1\) 到 \(n\) 的 \(\varphi\)，那可以先从 \(1 \sim n\) 循环求单个的 \(\varphi\) 值，然后输出打成表再在考试代码里整成数组，我们称之为【打表】（优 良 传 统）

\(Update\)：不要打表，不要打表，不要打表！！！(比赛时打表因为代码太长 \(CE\) 了。。而且交上去的时候没有提示。。。)

\(Update\)：可以打表。(打表拿了最优解的屑 \(\text{char_phi}\) 如是说) 但是欧拉函数还打表就没必要了(

---

\(概率\)

感觉这边好难啊焯

觉得概率期望很难受还是因为基础概念太多而且一下涌出来，很难短时间内记住吧（对我这种蒟蒻来说qAq）

还是大部分概念去虎哥博客看 我在这里写的就算自学概率期望的笔记吧、、

虎哥！！！

注意：一定把 \(\cup\) \(\cap\) \(|\) 什么的基础概念记清。。。这个还是比较重要的说

\(互斥事件\)

比如 {我和 \(\text{dbx}\) 一起吃饭}、{我孤单地吃饭} 两个事件，我不可能又孤单又和 \(\text{dbx}\) 一起吃，这俩事件就是互斥事件

而且阿互斥事件可以有很多个，和对立事件不一样

\(对立事件\)

比如午休 {卷}、{睡大觉}，假设只有这两种情况的话，那这俩就是对立事件

对立事件只能有两个，要么发生事件 \(A\) 要么发生事件 \(B\)，不可能 \(A\) 事件 \(B\) 事件都不发生

(当然无事发生也算一个事件的啦，但是无事发生可能属于事件B也可能属于事件A)

值得一提的是，对立事件属于互斥事件

\(独立事件\)

我们来康康虎哥的解释：

如果事件 \(A\) 是否发生对事件 \(B\) 发生的概率没有影响，同时事件 \(B\) 是否发生对事件 \(A\) 发生的概率也没有影响，则称 \(A\) 与 \(B\) 是相互独立事件}

比如一堆事件的可能性：{中午吃米饭}{今天午休卷数学}{今天下午大课间吃个橘子}{...}

中午吃米饭和我午休卷哪一科有什么关系吗？？没关系吧？？我午休卷个数学不会对下午大课间吃个橘子有影响吧？？

嗯　所以这俩是独立事件

具体而言，判断事件 \(A\) 与事件 \(B\) 是独立事件的条件就是 \(P(A \cap B) = P(A) \times P(B)\)

\(条件概率\)

\(P(A|B)\) 指的是 \(B\) 发生的情况下 \(A\) 发生的概率

这个东西对本蒟蒻来说还是挺难理解的，这玩意最本质的变化实际上就是样本空间的缩小

\(一堆公式\)

这一堆公式都挺好理解的，，但是问题就在于很可能用的时候想不起来，所以敲一遍加深印象

• 若 \(A\) 与 \(B\) 是互斥事件：\(P(A∪B) = P(A) + P(B)\)

• 若 \(A\) 与 \(B\) 是对立事件：\(P(A∩B) = 0,P(A∪B) = P(A) + P(B) = 1\)

• 互斥事件的可加性：\(P(A1∪A2∪A3∪...∪An) = P(A1) + P(A2) + ... + P(An)\)

• 独立事件的可乘性：\(P(A∩B) = P(A) × P(B)\) 这个就是生物计算遗传概率那个

• ⭐\(P(A|B) = P(A∩B) ÷ P(B)\)

于是就有了拓展公式们：

乘法公式：\(P(AB) = P(B|A) \cdot P(A) = P(A|B) \cdot P(B)\)

全概率公式：\(∀i, j, A_i \cap A_j = ∅\)，且 \(\sum_{i=1}^{n} { A_i } = 1\)，则有 \(P(B) = \sum_{i=1}^{n} { P(A_i) \cdot P(B|A_i) }\)

贝叶斯定理：啥我不会

---

瞎证明一下：

设\(Bi\)都是互斥事件

\(A = A∩Ω = A∩B_1 + A∩B_2 + ... + A∩B_n\)

即 \(A ⇔ A∩Ω ⇔ ΣA∩B_i\)

\(A∩B_i\) 显然和 \(A∩B_j\) 是互斥的阿，然后就想到了加法原理

\(P(A) = P(A∩Ω) = \sum P(A∩B_i)\)

\(P(A∩B_i)\) 可以用乘法公式，\(P(A∩B_i) = P(A|B_i) \times P(B_i)\)

所以就得到了\(P(A) = \sum P(A|B_i) × P(B_i)\)

"证毕"

贝叶斯公式 \(P(A|B) = \frac{ P(B|A) \times P(A) } { P(B) }\)

虎哥写的那个柿子：\(P(B_i|A) = \frac { P(B_i)P(A|B_i) } { \sum _ {j=1} ^ {n} { P(B_j)P(A|B_j) } }\)

虎哥写的那个式子我看不懂。。。

这啥 看不懂阿？？

度娘也这么说，但我真看不懂。。。

算了，先直接开期望吧

\(古典概型\)

三个特征：

• 试验的样本空间有限

• 实验中每个结果出现的可能性相同

• 这些随机现象所发生的事件是互斥的(扔骰子要么正要么反)

\(离散型随机变量\)

一听这名感觉挺 \(\text{upper-class}\)，，，实际上就是普通的变量吧？

有以下限制条件：

• 一定区间内变量的取值是有限个的

• 或者数值可以一一列举出来

\(\text{OI}\) 上求的期望大多是离散型随机变量的数学期望吧

---

\(期望\)

数学期望，可以理解为某件事情大量发生后的平均结果

怎么求呢？？？一个极其朴素的想法是大模拟好多好多次然后取平均值

当然了，这样会 \(\text{TLE}\) 加 \(\text{RE}\) 没准还 \(\text{MLE}\)，肯定不是这样啦

\(\text{so}\) 公式来力:

对一个离散随机变量 \(X\)，他的输出结果为 \(x_i\)；对于每个 \(x_i\) 对应的概率为 \(p_i\)，则他的数学期望：

\[E(x) = \sum_{i=1}^{n} X_i \cdot p_i \]

而且期望具有线性性：\(E(X+Y) = E(X)+E(Y)\)

还有可积性：\(E(X×Y) = E(X) \cdot E(Y)\)

这意味着啥？\(\text{dp}\) 阿！

是的，期望这边大多就是 \(\text{dp}\)

唔还有一件事，期望要倒叙推，概率要正序推，关于为什么，看这一段文字(\(\text{Ayaka}\) 教我的)

qwq

    // 然后听说要倒序
    // ？为什么
    // 然后kkkzuto跟我说 概率要正推 期望要逆推 他说他也不知道为什么，记住就行了
    // ？这什么定理？这啥啊？？
    // 然后我一脸为难地看着kkkzuto 他也一脸为难地看着whpq 然后whpq跟我说:
    /*
           ⚪
    ⚪     ⚪
           ⚪
           ⚪
    从一个往四个推，概率可以按比例分开，所以顺着推好推
    ⚪
    ⚪        ⚪
    ⚪
    ⚪
    从四个往一个推，也就是期望的累加，得把这四个情况都得到了才能往那一个推，比较麻烦
    这么着看还不明显，把一大堆递推树画出来就会发现难处了
    比如：
    ⚪
    ⚪      ⚪
    ⚪      
    ⚪              ⚪
    ⚪      ⚪
    ⚪
    ⚪      ⚪                  
    ⚪
    ⚪              ⚪        ⚪
    ⚪
    ⚪      ⚪
    ⚪
    ⚪      ⚪
    ⚪              ⚪
    ⚪      ⚪
    ⚪
    */

---

\(凸包\)

最近比赛有点多，我先改题

先咕掉

---

\(随机化\)

四种算法。都好屌的样子。然而没有多少人讲随机化，再加上机房的网只开一部分，导致我的资料十分有限。。

\(\text{Update}\)：我到现在都不会那四种算法，甚至不知道那是什么。

---

\(随机数的生成\)

我先不说那四种算法，说一下随机数

是时候扔掉 rand() 啦！之前搞一道题结果 rand() 循环了应该不到 \(\text{1e6}\) 次吧，\(\text{1000ms}\) 直接 \(\text{T}\) 掉

所以 mt19937 来了。

我直接引用 \(\text{OI-wiki}\)

mt19937
是一个随机数生成器类，效用同 rand()，随机数的范围同 unsigned int 类型的取值范围。
其优点是随机数质量高（一个表现为，出现循环的周期更长；其他方面也都至少不逊于 rand()），且速度比 rand() 快很多。使用时需要 #include<random>。
mt19937 基于 \(32\) 位梅森缠绕器，由松本与西村设计于 \(1998\) 年，使用时用其定义一个随机数生成器即可：std::mt19937 myrand(seed)，seed 可不填，不填 seed 则会使用默认随机种子。
mt19937 重载了 operator ()，需要生成随机数时调用 myrand() 即可返回一个随机数。
另一个类似的生成器是 mt19937_64，基于 \(64\) 位梅森缠绕器，由松本与西村设计于 \(2000\) 年，使用方式同 mt19937，但随机数范围扩大到了 unsigned long long 类型的取值范围。

好巨的样子。我只提取一下俺觉得比较有用的东西吧

• 比 \(rand()\) 的质量高

• 出现循环的周期更长

• 快！！！！！哦吼！！！

• 可以填一个 seed (伏笔

所以代码

mt19937

#include <iostream>
#include <random>
main(){
    std::mt19937 myrand(time(0));
    std::cout << myrand() << '\n';
    return 0;
}

还有比较重要的一点，注意这个是在 \(\text{C++11}\) 及以上才有的

\(\text{Update 2022.8.3}\)：
今天实测了了一下，可是 rand 竟然更快？？？？
不清楚为啥
不过殷教一直用这个，觉得问问殷教的意见

\(\text{Update}\)：殷教听了之后愣了一会，然后说这玩意随机数质量高

\(\text{random_device}\ 获取随机数种子\)

这个东西还行，不过有点小问题

还是直接上 \(\text{OI-wiki}\)

random_device 是一个基于硬件的均匀分布随机数生成器，在熵池耗尽 前可以高速生成随机数。该类在 \(\text{C++11}\) 定义，需要 random 头文件。由于熵池耗尽后性能急剧下降，所以建议用此方法生成 mt19937 等伪随机数的种子，而不是直接生成。

还记得熵吗？就是化学选择性必修一学的那个东西，好像是表示某一个东西的混乱度的。觉得这个就和随机数有点挂钩钩了

所以乖乖用 random_device 生成随机数种子罢

那么代码

qwq

#include <iostream>
#include <random>
signed main(){
    std::random_device rd;
    std::mt19937 char_phi(rd());
    std::cout << char_phi() << '\n';
    return 0;
}

感觉很玄学，我也不是专门研究这个语言的，但是为什么可以搞得跟宏定义一样。。

( 注：我看到百度文库的代码写的是 std::mt19937 gen(rd()) 这样子，然而我这么着写竟然也能编译运行成功，可能本来就能罢

\(Update\)：\(\text{joke3579}\) 说这玩意是一个类(好像是)，随便取名就行。

---

\(模拟退火算法\)

这听着就很美妙。然后我直接贴贴自为风月马前卒大佬的图

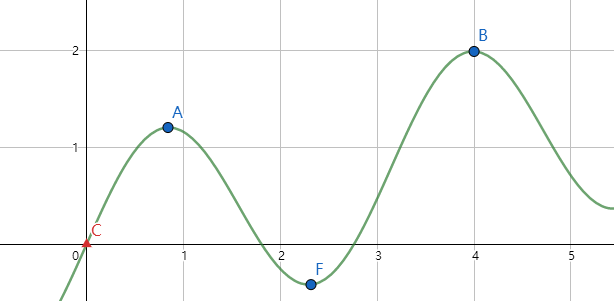
模拟退火是爬山算法的改进版，比如爬山算法可能只会找到局部最优解 \(\text{A}\) 致 \(\text{WA}\)

然而模拟退火有几率从 \(\text{A}\) 点跳出去从而找到全局最优解

贴贴 \(\text{rvalue}\) 大佬的动图

---

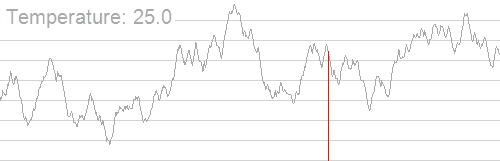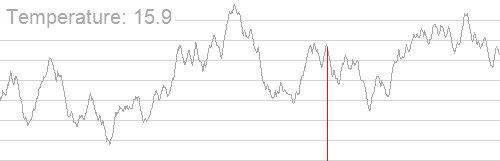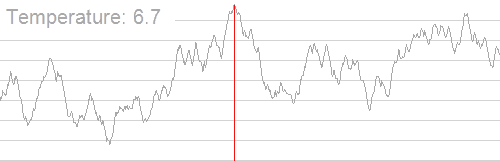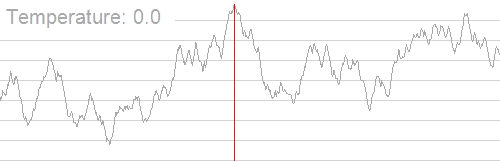
\(摩尔投票法\)

今天考了一个神题，我真服了，空间限制 \(\text{2MB}\)，时限 \(\text{500ms}\)
实际上就是一个摩尔投票的板子。不过我不会摩尔投票。。
空间不够开，那我就不开那么大，我直接开成大约 \(n\) 范围的 \(\frac{ 1 }{ 8 }\)
然后对输入数据进行以八分之一的概率随机选择，然后统计
卡着时间....\(30\)
\(\text{nmd}\) 主要是他加 \(\text{subtask}\)！！！

咳，说正题，摩尔投票，首先这个东西适用范围是 必须众数出现的次数 \(> \frac {n}{2}\)（注意要严格大于）

然后搞一个计数器 cnt，一个记录众数的 final_ans

首先如果 cnt == 0 那么就使 cnt = 1，并把当前数的值赋予 final_ans

然后继续往后扫，如果碰到了同样的数就 cnt ++，否则 cnt --。特殊地，cnt 减为 \(0\) 时应重新计数

最后 final_ans 就是那位众数

整个示例代码

code

int n, cnt, final_ans;
void work(){
    cin >> n;
    for(re i = 1, rs ; i <= n ; ++ i){
        cin >> rs;
        if(cnt == 0)
            cnt = 1, final_ans = rs;
        else {
            if(rs != final_ans)
                cnt --;
            else 
                cnt ++;
        }
    }
    cout << final_ans << '\n';
}

---

因为我太逊了，所以别的先咕着🕊