CS3402 Relational Design
Relational Design
Motivation
Student(StudentID, StudentName, CourseID, CourseName, Grade)
Design “anomalies”
-
Redundancy: StudentID => StudentName (captured multiple times)
-
Update anomaly: (Update facts in some places but not all)
-
Database Systems / DB Systems / DBS
-
Bob Lee / Robert Lee
-
- Deletion anomaly: (Inadvertently delete info)
- Deleting Alex also deletes CS4480 Data-Intensive Computing
Student(StudentID, StudentName, CourseID, CourseName, Grade) Better Design
-
Student(StudentID, StudentName)
-
Course(CourseID, CourseName)
-
Take(CourseID, Grade)
Functional Dependency
Examples:
- StudentID uniquely determines StudentName○ StudentID → Student Name
- CourseID uniquely determines CourseName○ CourseID → CourseName
Be careful: A → B does NOT imply B → A
Inference Rules for FDs
-
Given a set of FDs F, we can infer additional FDs that hold whenever the FDs in F hold
-
Armstrong's inference rules:
-
IR1: (Reflexive) If Y is a subset of X, then X → Y
-
IR2: (Augmentation) If X → Y, then XZ → YZ
-
IR3: (Transitive) If X → Y and Y → Z, then X → Z
-
-
IR1, IR2, IR3 form a sound and complete set of inference rules
-
Sound: These rules are true
-
Complete: All the other rules that are true can be deduced from these rules
-
- Additional Inference Rules
- Decomposition: If X →YZ, then X → Y and X → Z
- Union: if X → Y and X → Z, then X → YZ
- Pseudotransitivity: If X → Y and WY → Z, then WX → Z
-
Closure of a set F of FDs is the set F+ of all FDs that can be inferred from F
-
Closure of a set of attributes X with respect to F is the set X+ of all attributes that are functionally determined by X
-
X+ can be calculated by repeatedly applying IR1, IR2, IR3 using the FDs in F
Equivalence of Sets of FDs
-
Two sets of FDs F and G are equivalent if:
-
Every FD in F can be inferred from G, and
-
Every FD in G can be inferred from F
-
Hence, F and G are equivalent if F+ =G+
-
- There is a method for checking equivalence of sets of FDs
- Example:
-
-
F: A→BC
-
G: A→B, A→C
-
Normalization Theory
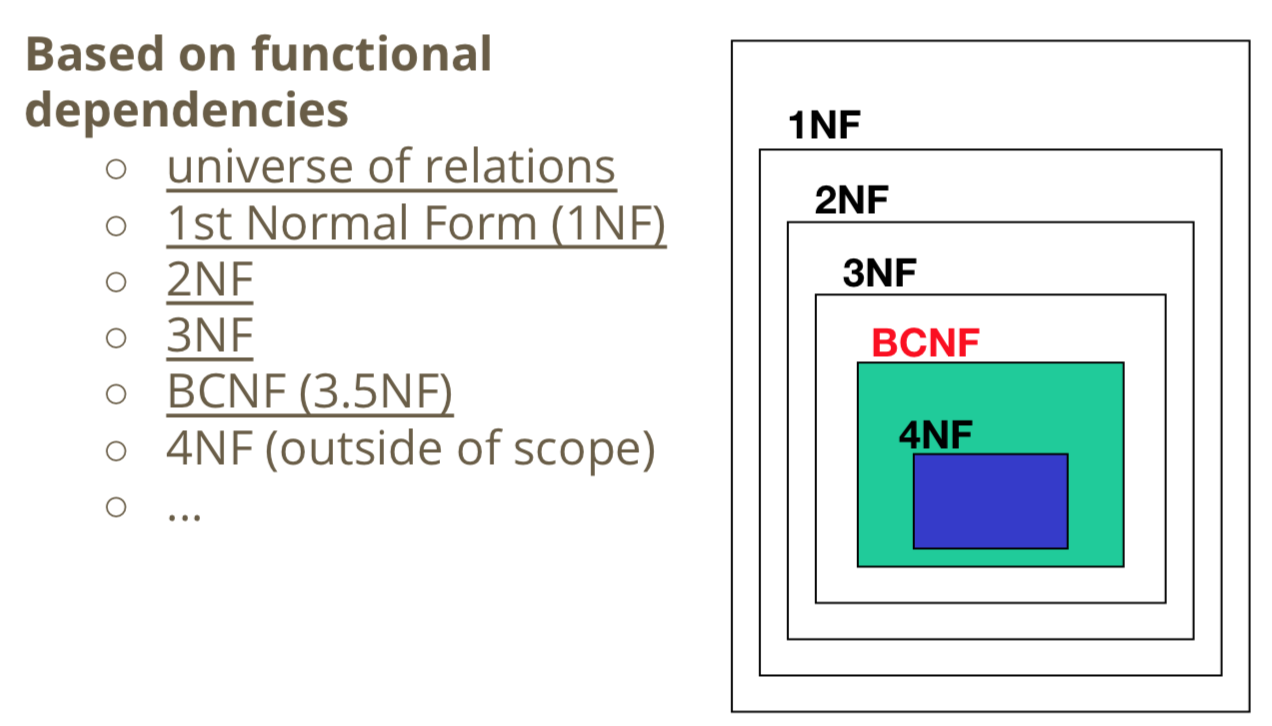
Desired Schema
-
Non-additive or lossless join: Extremely important
-
Preservation of the functional dependencies.
- Sometimes can be sacrificed
- Lossless join
- No spurious tuples (tuples that should not exist) should be generated by doing a natural-join of any relations
Relational DB Design
1NF
 PK is S#,P#
PK is S#,P#Problems with 1NF
- Insert Anomalies
- Inability to represent certain information: Eg, cannot enter “Supplier and City” information until Supplier supplies at least one part
- Delete Anomalies
- Deleting the “only tuple” for a supplier will destroy all the information about that supplier
- Update Anomalies
- “S# and City” could be redundantly represented for each P#, which may cause potential inconsistency when updating a tuple
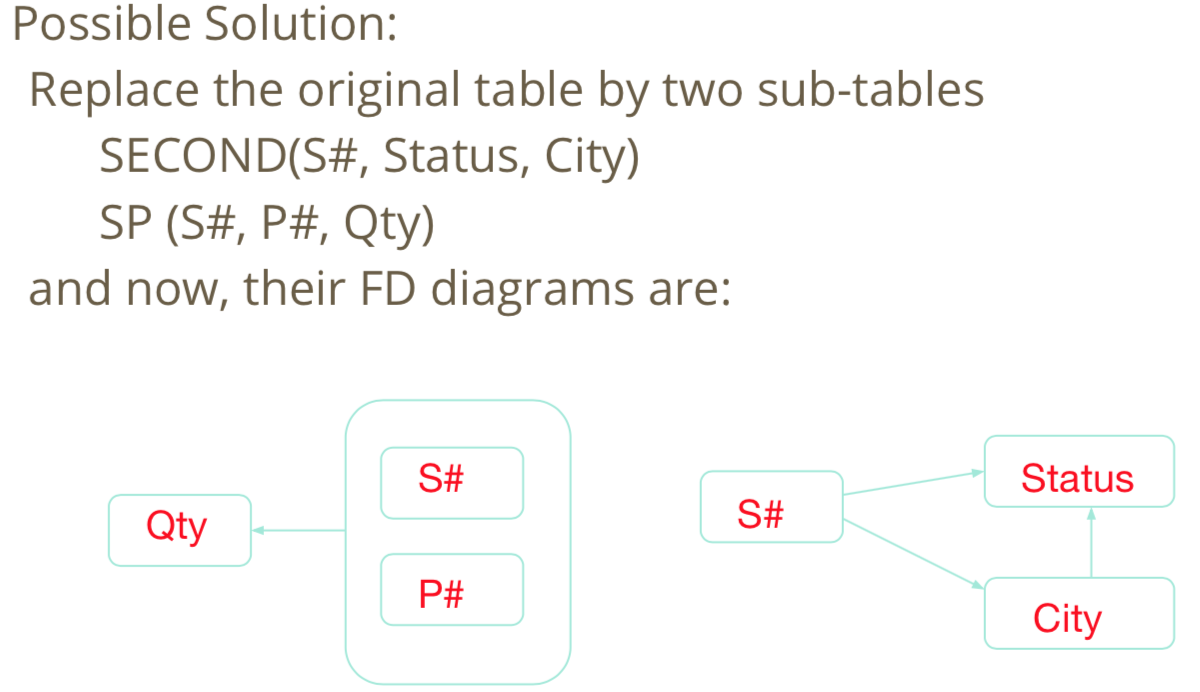
2NF


3NF

Normal Forms Defined Informally
- 1st normal form
- Each attribute is atomic
- 2nd normal form: removing partial dependencies
- Every non-prime attribute of the table is dependent on the whole of every candidate key
- 3rd normal form: removing transitive dependencies
- All the attributes in a table are determined only by the candidate keysof that table and not by any non-prime attributes
non-prime attribute: attribute that’s not part of a candidate key
BCNF
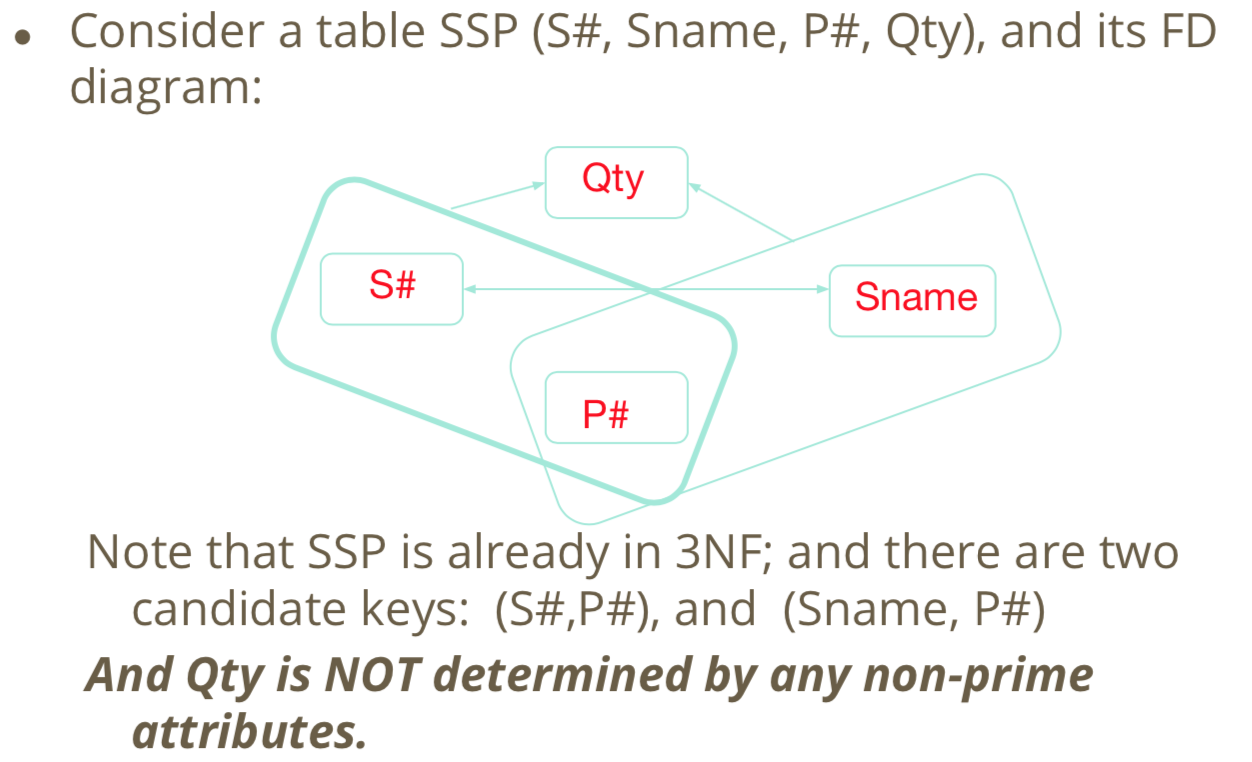



Example
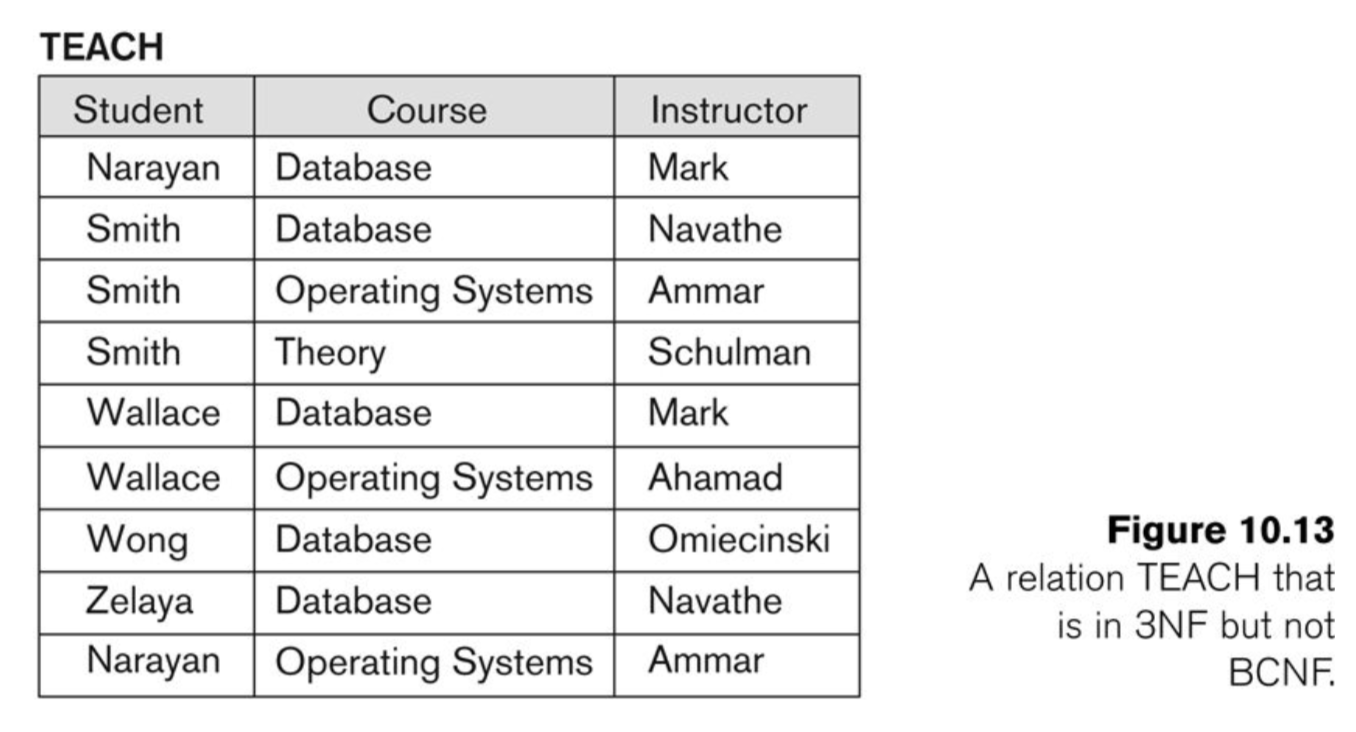


ER模型与关系模型
- 都是对数据的一种模型
- ER模型有很多的概念
实体Entities,关系relations,属性attributes等等
很好的满足了应用的需求
不适合计算机处理的需求
- 关系模型
只有一个概念:关系relation
物理世界是由一些表的集合组成的
很好地满足了计算机对数据的处理需求



数据建模完成之后, 可以把ER图转换成数据中的表 (关系建模)
1.实体的名字转换为表的名字
2.实体的属性转换为表中的列
3.具有唯一特点的属性设置为表中的主键
4.根据实体之间的关系设置为表中某列为外键列(主外键关联)
注意:第四步主要是:实体关系--->表关系
ER模型到关系表的映射
http://www.cnblogs.com/muchen/p/5265305.html
函数依赖(functional dependency)
函数依赖,是指关系中每行记录的某一列(或几列)的值唯一决定该条记录另一列的值。总的来说,有以下几种函数依赖:
1. 平凡函数依赖(trivial functional dependency)
是指一个或多个属性确定它自己,或者它的子集. 这种依赖在规范化中不会被用到.
2. 增广函数依赖(augmented functional dependency)
是指某个依赖式为真,则依赖式左侧,或者两侧同时增加某语句形成的一种依赖关系. 这种依赖在规范化中不会被用到。
3. 等价函数依赖(equivalent functional dependency)
这种依赖关系是一对对的。比如若A->B和B->A都为真,那么A能推出来的,B同样也能推出来,因此A->B和B->A就被称作等价函数依赖。这种依赖只需保留一组依赖关系即可,但它不属于规范化的范畴。
4. 部分函数依赖(partial functional dependency)
是指关系的一列函数依赖于组合主码的一部分。显然这种依赖只有组合主码才存在。这种依赖关系属于规范化范畴。
5. 完全函数依赖(full key functional dependency)
是指复合主码函数确定关系中的其他列,并且复合主码的任意部分不能单独确定其他列。这个概念和上面的部分函数依赖显然是对立的。这种依赖关系属于规范化范畴。
6. 传递函数依赖(transitive functional dependency)
是指非码列函数确定关系中的其他非码列。这种依赖关系属于规范化范畴。
这六种函数依赖中只有后面三种和规范化设计有关。前面三种则因为对改进冗余信息并没有帮助,不纳入规范化过程中。
设计关系数据库时,遵从不同的规范要求,才能设计出合理的关系型数据库,这些不同的规范要求被称为不同的范式,各种范式呈递次规范,越高的范式数据库冗余越小。一个关系是否满足某种范式通常要看它是否不包含某个函数依赖。
目前关系数据库有六种范式:
第一范式(1NF)
第二范式(2NF)
第三范式(3NF)
巴斯-科德范式(BCNF)
第四范式(4NF)
第五范式(5NF,又称完美范式)
注:满足最低要求的范式是第一范式(1NF)。在第一范式的基础上进一步满足更多规范要求的称为第二范式(2NF),其余范式以次类推。一般说来,数据库只需满足第三范式(3NF)就行了
第一范式:
一个表中, 每个列里面的值是不能再分割的. 即一个表中每一行都是唯一, 并且任何行都没有包含多个值的列,则它满足1NF.
例如:我们设计的表中有一个列是:爱好
这个列的值可能会是这样:足球篮球乒乓球
但是这值是可以再分割的:足球、篮球、乒乓球
所以这种设计是不满足第一范式
第二范式:
第二范式是在满足第一范式的基础上
表中的非主键列都必须依赖于主键列(不包含部分函数依赖)
例如:
订单表: 订单编号 是主键
订单编号 订单名称 订单日期 订单中产品的生产地
这几个非主键列中,产品生产地是不依赖于订单编号的,所以这种设计是不满足第二范式
第三范式:
第三范式是在满足第二范式的基础上
表中的非主键列都必须直接依赖于主键列, 而不能间接的依赖. (不包含传递函数依赖)
(不能产生依赖传递)
例如:
订单表: 订单编号 是主键
订单编号 订单名称 顾客编号 顾客姓名
顾客编号依赖于订单编号,顾客姓名依赖于顾客编号,从而顾客姓名间接的依赖于订单编号,那么这里产生了依赖传递,所以这个设计是不满足第三范式的
第一范式 1NF 属性不可再分割,符合原子性。 没什么好解释的,地球人都明白 第二范式 2NF 在1NF的基础上: 不允许出现有field部分依赖于主键(或者说依赖于主键的一部分) 官方说法:数据库表中不存在非关键字段对任一候选关键字段的部分函数依赖(部分函数依赖指的是存在组合关键字中的某些字段决定非关键字段的情况),也即所有非关键字段都完全依赖于整组候选关键字。 Allen解释一下:比如一张表是(A, B, C, D),其中(A, B)是主键,如果存在B->C就违反了2NF,因为C只需要主键的一部分就可以被决定了 第三范式 3NF 在2NF的基础上: 不允许出现可传递的依赖关系(transitive dependencies) 官方说法:在第二范式的基础上,数据表中如果不存在非关键字段对关键字段的传递函数依赖则符合第三范式。所谓传递函数依赖,指的是如果存在"A → B → C"的决定关系,则C传递函数依赖于A 很容易理解,Kiza同学说这是人类的常识。 Boyce-Codd范式 BCNF 在3NF的基础上: 不允许出现有主键的一部分被主键另一部分或者其他部分决定 另一种说法:Left side of every non-trivial FD must contains a key 每个非平凡FD的左边必须有一个主键 BCNF,表中的每个决定因子是候选键。如果只有一个候选键,则3NF和BCNF相同 网友们通常喜欢用的一个例子: 假设仓库管理关系表为StorehouseManage(仓库ID, 存储物品ID, 管理员ID, 数量),且有一个管理员只在一个仓库工作;一个仓库可以存储多种物品。这个数据库表中存在如下决定关系: (仓库ID, 存储物品ID) →(管理员ID, 数量) (管理员ID, 存储物品ID) → (仓库ID, 数量) 所以,(仓库ID, 存储物品ID)和(管理员ID, 存储物品ID)都是StorehouseManage的候选关键字,表中的唯一非关键字段为数量,它是符合第三范式的。但是,由于存在如下决定关系: (仓库ID) → (管理员ID) (管理员ID) → (仓库ID) 也就是说,(仓库ID, 存储物品ID)这个主键中的仓库ID可以被管理员ID决定,同样(管理员ID, 存储物品ID)中管理员ID也可以被仓库ID决定,所以此表应该拆分。 3NF->BCNF的步骤: 1. 一个表,从所给的FD中,找出一个FD左边没有key的 2. 给这个FD的右边补全属性(field)。 3. 此时得到两个表,一个是第2步中得到的FD中的表,另一个是第2步中FD的所有左边 及 其他所有没有在这个FD中出现的属性组成的表 4. 投影总的FD分别到两个表 如果仍然有表violation,继续分解 例如: 表(Name, Location, Application, Provider, FavAppl) FD: Name->Location, Name->FavAppl, Application->Provider Key: Name, Application 1. Name->Location的左边没有key。 2. 将其补充。Name->Location, Name->FavAppl,因此得到表(Name, Location, FavAppl) 3. 一个表是(Name, Location, FavAppl)。另一个表,”第2步中FD的所有左边“是指Name,“其他所有没有在这个FD中出现的属性”是指Application和 Provider。因此第二个表是(Name, Application, Provider) 4. 第二个表中,Application->Provider的左边没有key,继续分解第二个表 最终结果,原表分为了(Name, Location, Provider),(Application, Provider),(Application, Name) 总结: 1NF | 消除非主属性对码的部分依赖 2NF | 消除非主属性对码的传递依赖 3NF | 消除主属性对码的部分和传递依赖 BCNF
链接:https://www.zhihu.com/question/24696366/answer/29189700
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
国内绝大多数院校用的王珊的《数据库系统概论》这本教材,某些方面并没有给出很详细很明确的解释,与实际应用联系不那么紧密,你有这样的疑问也是挺正常的。我教《数据库原理》这门课有几年了,有很多学生提出了和你一样的问题,试着给你解释一下吧。(基本来自于我上课的内容,某些地方为了不过于啰嗦,放弃了一定的严谨,主要是在“关系”和“表”上)
首先要明白”范式(NF)”是什么意思。按照教材中的定义,范式是“符合某一种级别的关系模式的集合,表示一个关系内部各属性之间的联系的合理化程度”。很晦涩吧?实际上你可以把它粗略地理解为一张数据表的表结构所符合的某种设计标准的级别。就像家里装修买建材,最环保的是E0级,其次是E1级,还有E2级等等。数据库范式也分为1NF,2NF,3NF,BCNF,4NF,5NF。一般在我们设计关系型数据库的时候,最多考虑到BCNF就够。符合高一级范式的设计,必定符合低一级范式,例如符合2NF的关系模式,必定符合1NF。
接下来就对每一级范式进行一下解释,首先是第一范式(1NF)。
符合1NF的关系(你可以理解为数据表。“关系模式”和“关系”的区别,类似于面向对象程序设计中”类“与”对象“的区别。”关系“是”关系模式“的一个实例,你可以把”关系”理解为一张带数据的表,而“关系模式”是这张数据表的表结构。1NF的定义为:符合1NF的关系中的每个属性都不可再分。表1所示的情况,就不符合1NF的要求。
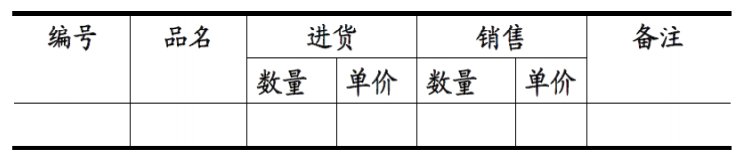
表1
实际上,1NF是所有关系型数据库的最基本要求,你在关系型数据库管理系统(RDBMS),例如SQL Server,Oracle,MySQL中创建数据表的时候,如果数据表的设计不符合这个最基本的要求,那么操作一定是不能成功的。也就是说,只要在RDBMS中已经存在的数据表,一定是符合1NF的。如果我们要在RDBMS中表现表中的数据,就得设计为表2的形式:

表2
但是仅仅符合1NF的设计,仍然会存在数据冗余过大,插入异常,删除异常,修改异常的问题,例如对于表3中的设计:
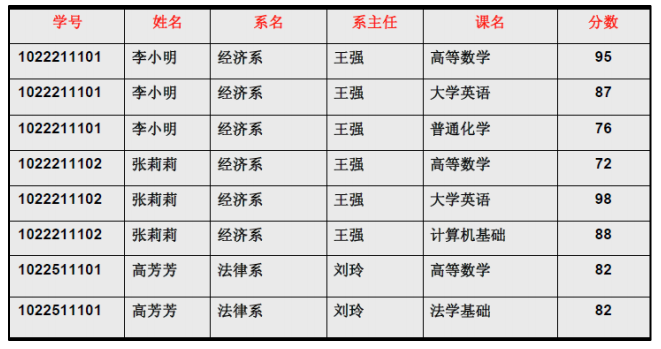
表3
- 每一名学生的学号、姓名、系名、系主任这些数据重复多次。每个系与对应的系主任的数据也重复多次——数据冗余过大
- 假如学校新建了一个系,但是暂时还没有招收任何学生(比如3月份就新建了,但要等到8月份才招生),那么是无法将系名与系主任的数据单独地添加到数据表中去的 (注1)——插入异常
注1:根据三种关系完整性约束中实体完整性的要求,关系中的码(注2)所包含的任意一个属性都不能为空,所有属性的组合也不能重复。为了满足此要求,图中的表,只能将学号与课名的组合作为码,否则就无法唯一地区分每一条记录。
注2:码:关系中的某个属性或者某几个属性的组合,用于区分每个元组(可以把“元组”理解为一张表中的每条记录,也就是每一行)。 - 假如将某个系中所有学生相关的记录都删除,那么所有系与系主任的数据也就随之消失了(一个系所有学生都没有了,并不表示这个系就没有了)。——删除异常
- 假如李小明转系到法律系,那么为了保证数据库中数据的一致性,需要修改三条记录中系与系主任的数据。——修改异常。
正因为仅符合1NF的数据库设计存在着这样那样的问题,我们需要提高设计标准,去掉导致上述四种问题的因素,使其符合更高一级的范式(2NF),这就是所谓的“规范化”。
第二范式(2NF)在关系理论中的严格定义我这里就不多介绍了(因为涉及到的铺垫比较多),只需要了解2NF对1NF进行了哪些改进即可。其改进是,2NF在1NF的基础之上,消除了非主属性对于码的部分函数依赖。接下来对这句话中涉及到的四个概念——“函数依赖”、“码”、“非主属性”、与“部分函数依赖”进行一下解释。
函数依赖
我们可以这么理解(但并不是特别严格的定义):若在一张表中,在属性(或属性组)X的值确定的情况下,必定能确定属性Y的值,那么就可以说Y函数依赖于X,写作 X → Y。也就是说,在数据表中,不存在任意两条记录,它们在X属性(或属性组)上的值相同,而在Y属性上的值不同。这也就是“函数依赖”名字的由来,类似于函数关系 y = f(x),在x的值确定的情况下,y的值一定是确定的。
例如,对于表3中的数据,找不到任何一条记录,它们的学号相同而对应的姓名不同。所以我们可以说姓名函数依赖于学号,写作 学号 → 姓名。但是反过来,因为可能出现同名的学生,所以有可能不同的两条学生记录,它们在姓名上的值相同,但对应的学号不同,所以我们不能说学号函数依赖于姓名。表中其他的函数依赖关系还有如:
- 系名 → 系主任
- 学号 → 系主任
- (学号,课名) → 分数
但以下函数依赖关系则不成立:
- 学号 → 课名
- 学号 → 分数
- 课名 → 系主任
- (学号,课名) → 姓名
从“函数依赖”这个概念展开,还会有三个概念:
完全函数依赖
在一张表中,若 X → Y,且对于 X 的任何一个真子集(假如属性组 X 包含超过一个属性的话),X ' → Y 不成立,那么我们称 Y 对于 X 完全函数依赖,记作 X F→ Y。(那个F应该写在箭头的正上方,没办法打出来……,正确的写法如图1)
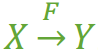
图1
例如:
- 学号 F→ 姓名
- (学号,课名) F→ 分数 (注:因为同一个的学号对应的分数不确定,同一个课名对应的分数也不确定)
部分函数依赖
假如 Y 函数依赖于 X,但同时 Y 并不完全函数依赖于 X,那么我们就称 Y 部分函数依赖于 X,记作 X P→ Y,如图2。
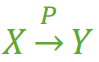
图2
例如:
- (学号,课名) P→ 姓名
传递函数依赖
假如 Z 函数依赖于 Y,且 Y 函数依赖于 X (感谢
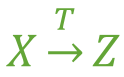
图3
码
设 K 为某表中的一个属性或属性组,若除 K 之外的所有属性都完全函数依赖于 K(这个“完全”不要漏了),那么我们称 K 为候选码,简称为码。在实际中我们通常可以理解为:假如当 K 确定的情况下,该表除 K 之外的所有属性的值也就随之确定,那么 K 就是码。一张表中可以有超过一个码。(实际应用中为了方便,通常选择其中的一个码作为主码)
例如:
对于表3,(学号、课名)这个属性组就是码。该表中有且仅有这一个码。(假设所有课没有重名的情况)
非主属性
包含在任何一个码中的属性成为主属性。
例如:
对于表3,主属性就有两个,学号与 课名。
终于可以回过来看2NF了。首先,我们需要判断,表3是否符合2NF的要求?根据2NF的定义,判断的依据实际上就是看数据表中是否存在非主属性对于码的部分函数依赖。若存在,则数据表最高只符合1NF的要求,若不存在,则符合2NF的要求。判断的方法是:
第一步:找出数据表中所有的码。
第二步:根据第一步所得到的码,找出所有的主属性。
第三步:数据表中,除去所有的主属性,剩下的就都是非主属性了。
第四步:查看是否存在非主属性对码的部分函数依赖。
对于表3,根据前面所说的四步,我们可以这么做:
第一步:
- 查看所有每一单个属性,当它的值确定了,是否剩下的所有属性值都能确定。
- 查看所有包含有两个属性的属性组,当它的值确定了,是否剩下的所有属性值都能确定。
- ……
- 查看所有包含了六个属性,也就是所有属性的属性组,当它的值确定了,是否剩下的所有属性值都能确定。
看起来很麻烦是吧,但是这里有一个诀窍,就是假如A是码,那么所有包含了A的属性组,如(A,B)、(A,C)、(A,B,C)等等,都不是码了(因为作为码的要求里有一个“完全函数依赖”)。
图4表示了表中所有的函数依赖关系:
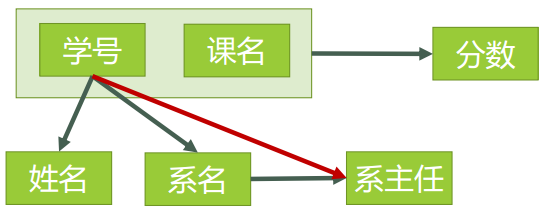
图4
这一步完成以后,可以得到,表3的码只有一个,就是(学号、课名)。
第二步:
主属性有两个:学号 与课名
第三步:
非主属性有四个:姓名、系名、系主任、分数
第四步:
对于(学号,课名) → 姓名,有 学号 → 姓名,存在非主属性 姓名 对码(学号,课名)的部分函数依赖。
对于(学号,课名) → 系名,有 学号 → 系名,存在非主属性 系名 对码(学号,课名)的部分函数依赖。
对于(学号,课名) → 系主任,有 学号 → 系主任,存在非主属性 对码(学号,课名)的部分函数依赖。
所以表3存在非主属性对于码的部分函数依赖,最高只符合1NF的要求,不符合2NF的要求。
为了让表3符合2NF的要求,我们必须消除这些部分函数依赖,只有一个办法,就是将大数据表拆分成两个或者更多个更小的数据表,在拆分的过程中,要达到更高一级范式的要求,这个过程叫做”模式分解“。模式分解的方法不是唯一的,以下是其中一种方法:
选课(学号,课名,分数)
学生(学号,姓名,系名,系主任)
我们先来判断以下,选课表与学生表,是否符合了2NF的要求?
对于选课表,其码是(学号,课名),主属性是学号和课名,非主属性是分数,学号确定,并不能唯一确定分数,课名确定,也不能唯一确定分数,所以不存在非主属性分数对于码 (学号,课名)的部分函数依赖,所以此表符合2NF的要求。
对于学生表,其码是学号,主属性是学号,非主属性是姓名、系名和系主任,因为码只有一个属性,所以不可能存在非主属性对于码 的部分函数依赖,所以此表符合2NF的要求。
图5表示了模式分解以后的新的函数依赖关系
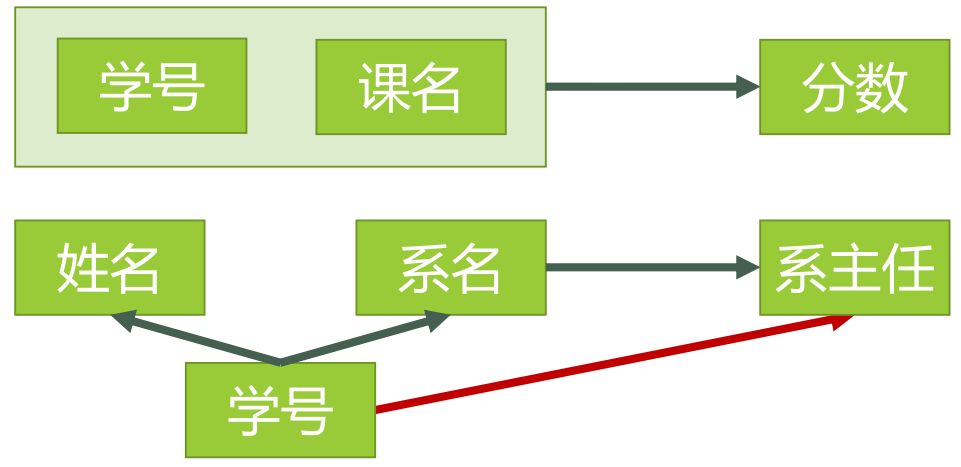
图5
表4表示了模式分解以后新的数据
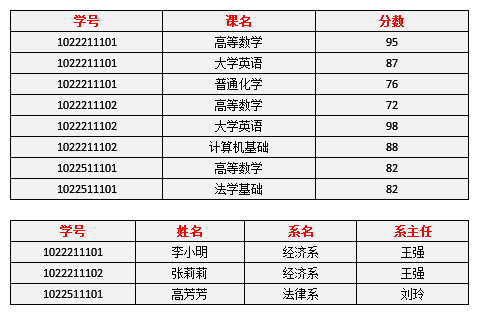
表4
(这里还涉及到一个如何进行模式分解才是正确的知识点,先不介绍了)
现在我们来看一下,进行同样的操作,是否还存在着之前的那些问题?
- 李小明转系到法律系
只需要修改一次李小明对应的系的值即可。——有改进 - 数据冗余是否减少了?
学生的姓名、系名与系主任,不再像之前一样重复那么多次了。——有改进 - 删除某个系中所有的学生记录
该系的信息仍然全部丢失。——无改进 - 插入一个尚无学生的新系的信息。
因为学生表的码是学号,不能为空,所以此操作不被允许。——无改进
所以说,仅仅符合2NF的要求,很多情况下还是不够的,而出现问题的原因,在于仍然存在非主属性系主任对于码学号的传递函数依赖。为了能进一步解决这些问题,我们还需要将符合2NF要求的数据表改进为符合3NF的要求。
第三范式(3NF)3NF在2NF的基础之上,消除了非主属性对于码的传递函数依赖。也就是说, 如果存在非主属性对于码的传递函数依赖,则不符合3NF的要求。
接下来我们看看表4中的设计,是否符合3NF的要求。
对于选课表,主码为(学号,课名),主属性为学号和课名,非主属性只有一个,为分数,不可能存在传递函数依赖,所以选课表的设计,符合3NF的要求。
对于学生表,主码为学号,主属性为学号,非主属性为姓名、系名和系主任。因为 学号 → 系名,同时 系名 → 系主任,所以存在非主属性系主任对于码学号的传递函数依赖,所以学生表的设计,不符合3NF的要求。。
为了让数据表设计达到3NF,我们必须进一步进行模式分解为以下形式:
选课(学号,课名,分数)
学生(学号,姓名,系名)
系(系名,系主任)
对于选课表,符合3NF的要求,之前已经分析过了。
对于学生表,码为学号,主属性为学号,非主属性为系名,不可能存在非主属性对于码的传递函数依赖,所以符合3NF的要求。
对于系表,码为系名,主属性为系名,非主属性为系主任,不可能存在非主属性对于码的传递函数依赖(至少要有三个属性才可能存在传递函数依赖关系),所以符合3NF的要求。。
新的函数依赖关系如图6
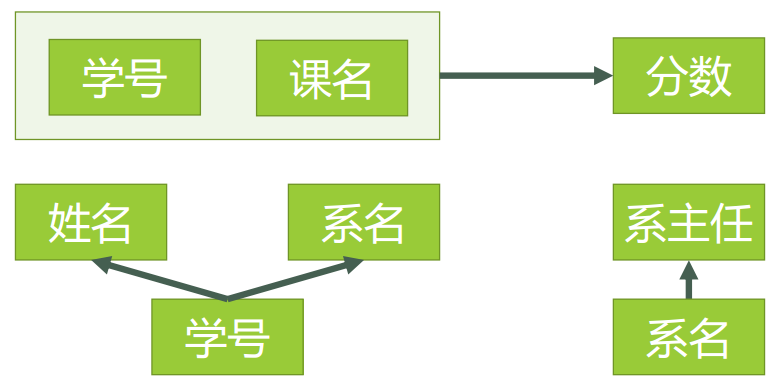
图6
新的数据表如表5
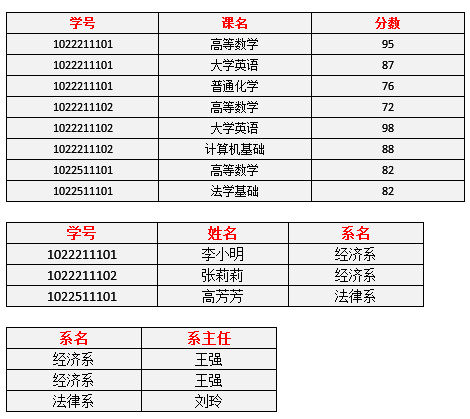
表5
现在我们来看一下,进行同样的操作,是否还存在着之前的那些问题?
- 删除某个系中所有的学生记录
该系的信息不会丢失。——有改进 - 插入一个尚无学生的新系的信息。
因为系表与学生表目前是独立的两张表,所以不影响。——有改进 - 数据冗余更加少了。——有改进
结论
由此可见,符合3NF要求的数据库设计,基本上解决了数据冗余过大,插入异常,修改异常,删除异常的问题。当然,在实际中,往往为了性能上或者应对扩展的需要,经常 做到2NF或者1NF,但是作为数据库设计人员,至少应该知道,3NF的要求是怎样的。
==============时隔半年,终于决定把这个坑填上,来晚了 ===========
BCNF范式
要了解 BCNF 范式,那么先看这样一个问题:
若:
- 某公司有若干个仓库;
- 每个仓库只能有一名管理员,一名管理员只能在一个仓库中工作;
- 一个仓库中可以存放多种物品,一种物品也可以存放在不同的仓库中。每种物品在每个仓库中都有对应的数量。
那么关系模式 仓库(仓库名,管理员,物品名,数量) 属于哪一级范式?
答:已知函数依赖集:仓库名 → 管理员,管理员 → 仓库名,(仓库名,物品名)→ 数量
码:(管理员,物品名),(仓库名,物品名)
主属性:仓库名、管理员、物品名
非主属性:数量
∵ 不存在非主属性对码的部分函数依赖和传递函数依赖。∴ 此关系模式属于3NF。
基于此关系模式的关系(具体的数据)可能如图所示:
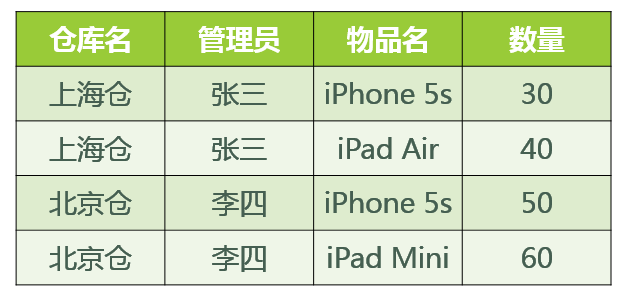
好,既然此关系模式已经属于了 3NF,那么这个关系模式是否存在问题呢?我们来看以下几种操作:
- 先新增加一个仓库,但尚未存放任何物品,是否可以为该仓库指派管理员?——不可以,因为物品名也是主属性,根据实体完整性的要求,主属性不能为空。
- 某仓库被清空后,需要删除所有与这个仓库相关的物品存放记录,会带来什么问题?——仓库本身与管理员的信息也被随之删除了。
- 如果某仓库更换了管理员,会带来什么问题?——这个仓库有几条物品存放记录,就要修改多少次管理员信息。
从这里我们可以得出结论,在某些特殊情况下,即使关系模式符合 3NF 的要求,仍然存在着插入异常,修改异常与删除异常的问题,仍然不是 ”好“ 的设计。
造成此问题的原因:存在着主属性对于码的部分函数依赖与传递函数依赖。(在此例中就是存在主属性【仓库名】对于码【(管理员,物品名)】的部分函数依赖。
解决办法就是要在 3NF 的基础上消除主属性对于码的部分与传递函数依赖。
仓库(仓库名,管理员)
库存(仓库名,物品名,数量)
这样,之前的插入异常,修改异常与删除异常的问题就被解决了。
以上就是关于 BCNF 的解释。
最近身体不太舒服,写不动了。有空再放几个典型习题及其解答吧。
===============================
问题1:
李德竹:老师您好,我看了您关于数据库范式的回答,有一点不太理解,就是关于码的定义,如果除K之外的所有属性都完全函数依赖于K时才能称K为码,那么在判断2NF时又怎么会存在非主属性对码的部分函数依赖这种情况?希望老师有时间能指点一下,谢谢
我 :在“码”的定义中,除 K 之外的所有属性应该看成是一个集合 U(也就是一个整体),也就是说,只有 K 能够完全函数决定 U 中的每一个属性,那么 K 才是码。如果 K 只是能够完全函数决定 U 中的一部分属性,而不能完全函数决定另外一部分属性,那么 K 不是码。
比如有关系模式 R (Sno, Sname, Cno, Cname, Sdept, Sloc, Grade),其中函数依赖集为 F= {
Sno → Sname, Sno → Sdept, Sdept → Sloc,Sno → Sloc, Cno → Cname, (Sno, Cno) → Grade }
那么 R 中的码只能是 (Sno, Cno),Sno 或 Cno 并不能完全函数决定除 Sno / Cno 之外的所有其他属性(其实就是不能决定 Grade ),所以单独的 Sno 与 Cno 并不能作为码。
所以可得到主属性:Sno, Cno
非主属性:Sname, Cname, Sdept, Sloc, Grade
R 中存在非主属性 Cname 对于码 (Sno, Cno) 的部分函数依赖 (Cno → Cname) 。(还有很多别的例子就不一一列举了)。所以 R 不符合 2NF 的要求


 浙公网安备 33010602011771号
浙公网安备 33010602011771号