CS3334 Lecture 3
Arrays, Linked Lists, Stacks & Queues
Introduction
How to store and organize data in a computer so that the data can be managed efficiently.
-Representation of data
-Algorithms (methods) for managing data (usually include search, insert, delete, and update)
Efficiency is important
Focus on main memory data storage; data storage in secondary storage (e.g., hard disks and databases) is usually called indexing structures
Array
Array is a data structure that arranges items at equally spaced addresses in computer memory
int foo[7]
Unsorted Arrays
Pros:
- Array elements can be accessed by specifying the array name followed by the index in square brackets. Eg foo[2] is 8
- Efficient for insertion by appending a new element.
Cons:
- Have to scan through the whole array to determine for sure if an item is not there
Sorted Arrays
Pros:
- Efficient for searching
Cons:
- Have to move all items behind the point of insertion to make room for the new one
Linked Lists
A linked list is a data structure that allows both efficient searching and insertion/deletion.
A collection of items linked in a sequence:
![]()
Pros:
-
Easy to insert/delete items in the middle, provided we know where to insert/delete (a sorted linked list can easily be maintained.)
Cons:
-
Difficult to access the i-th item, given an arbitrary i
Linked Lists: Node
struct Node { Node(): next(NULL) {} Node(int newData): data(newData), next(NULL) {} Item data; // Item is a generic data type Node* next; };

Linked Lists: Traversing (non-circular)
// Suppose head points to the 1st node of a list Node* p = head; while (p!=0) { // process p->data p = p->next; }
Linked Lists: Insert a Node
// To insert a node after the node pointed to by p. // newData is a variable of type Item 1. Node *temp = new Node(newData); 2. temp->next = p->next; 3. p->next = temp;
1. 2.
2. 3.
3.
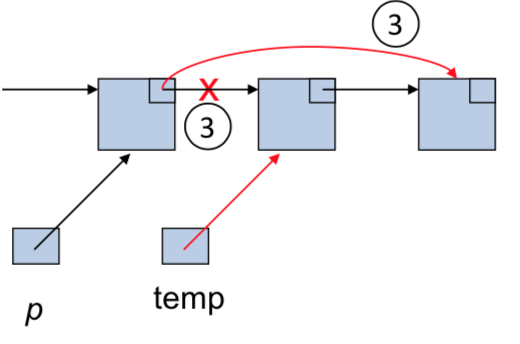
Linked Lists: Delete a Node
// To delete a node after the node pointed to by p // var. retData to retrieve content of deleted node 1. Node *temp = p->next; 2. retData = temp->data; 3. p->next = temp->next; 4. delete temp;
1. 3.
3.
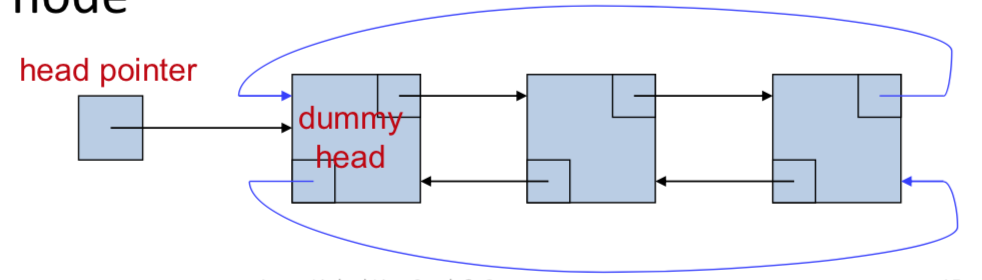
Variations of Linked Lists
- Singly- / doubly-linked
- With / without dummy head node
- Circular / non-circular
E.g., a circular doubly-linked list with a dummy head node
E.g., a non-circular doubly-linked list without a dummy head node

E.g., a non-circular singly-linked list without a dummy head node

Stacks
A stack is a sequence of elements in which update can only happen at one end of the sequence, called the top.
Operations supported:
– push(x): add an element x to the top
– pop(x): remove the top element and return it in x, i.e., first-in-last-out (FILO)
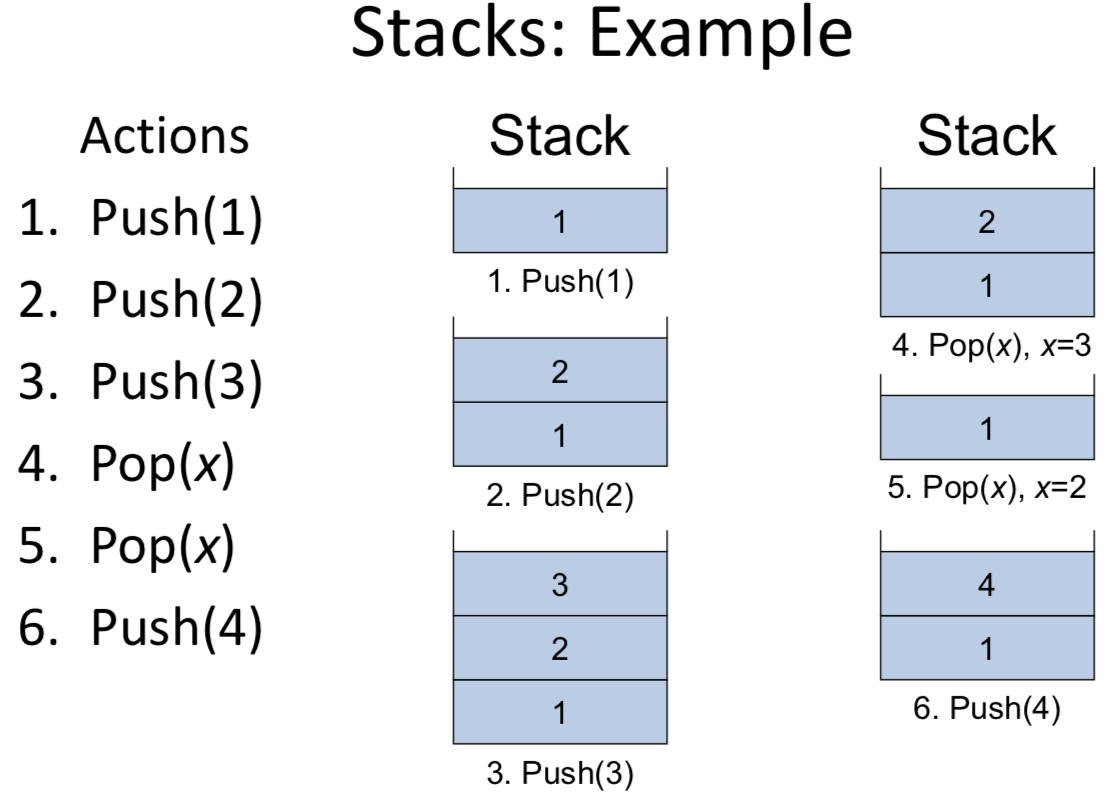
Array implementation of stack:
– Maintain size, i.e., the number of elements in stack
– Elements stored in A[0..size-1]
- The oldest one at A[0] is called bottom of stack
- The newest one at A[size-1] is called top of stack
– push(x):
- Store x at A[size]; then increase size by 1
– pop(x):
- If size = 0, return “Empty Stack”, otherwise decrease size by 1 and store A[size] in x
The method of choosing the size of array A[] (As we insert more and more, eventually the array will be full) - A dynamic array
- Maintain capacity of A[]
- Double capacity when capacity=size (i.e. full)
- Half capacity when size≤capacity/4
Stacks: C++ Code
class Stack { public: Stack(int initCap=100); Stack(const Stack& rhs); ~Stack();
void push(Item x);
void pop(Item& x); private: void realloc(int newCap); Item* array; int size; int cap; };
void Stack::push(Item x) { if (size==cap) realloc(2*cap); array[size++]=x; } // An internal func. to support resizing of array void Stack::realloc(int newCap) { if (newCap < size) return; Item *oldarray = array; //oldarray is “point to” array array = new Item[newCap]; //create new space for array //with a size of newCap for (int i=0; i<size; i++) array[i] = oldarray[i]; cap = newCap; delete [] oldarray;
}
void Stack::pop(Item& x) { if (size==0) x=EmptyStack; // assume EmptyStack is a special value else { x=array[--size]; if (size <= cap/4) realloc(cap/2); } }
Stack: Time complexity
-
Let n = current number of elements in the stack; n changes as pushes/pops are performed
-
Excluding the time for expanding/shrinking the array, push() and pop() need O(1) time in the worst case
-
Array expanding/shrinking is costly (O(n) time) but is needed once after at least n/2 operations
- E.g., initial cap is 4, after 5 push operations
- size = n = 5, cap = 8, n/2 = 2.5
- Need ≥ 4 more push operations to trigger array expanding
- Need ≥ 3 more pop operations to trigger array shrinking
Stacks: Space Complexity
-
When there are n elements in a stack, the largest required capacity of the stack is 4n. E.g., when size=n=2, the largest required capacity cap=8 (just before shrinking).
-
Space allocated for array A[0..cap-1] is: ≤ max{100, 4n}
Therefore, the space complexity is S(n) = O(n).
Linked list implementation of stack:
- May use a circular doubly-linked list
- push(x): call insertFront(x)
- pop(x): if stack not empty, call deleteFront(x)
Conclusion:
Both array and linked-list implementations are efficient:
- Excluding array expansion/shrinking, all operations take O(1) time in the worst case
Queues
A queue is a list of elements in which insertion can only be done at one end and deletion at the other.
Operations supported:
– EnQueue(x): insert element x at the end
– DeQueue(x): delete the front element and return it in x, i.e., first-in-first-out (FIFO)
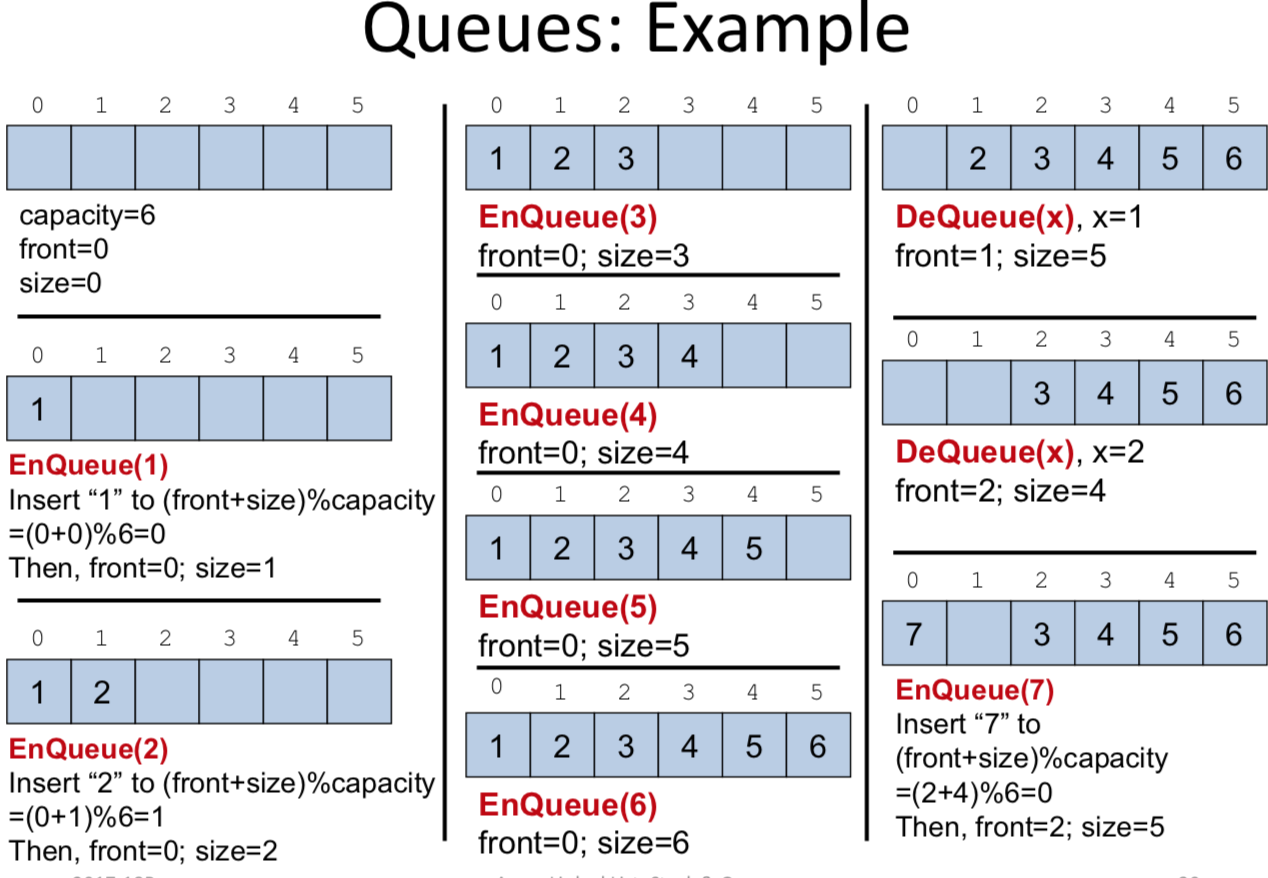
Circular array implementation of queue:
- Maintain 2 variables: front and size
- Elements stored in A[front..front+size-1], the oldest element at A[front], the newest element at A[front+size-1]
- Wrap around the array, if necessary, using “%capacity”. (front+size)%capacity
- EnQueue(x):
- Store x at A[(front+size)%capacity] and increase size by 1
- DeQueue(x):
-
If queue is not empty, copy A[front] to x, increase front by 1 and decrease size by 1
-
- Whenever front becomes ≥ capacityof A[], subtract front by capacity, i.e., front=front-capacity.
Linked list implementation of queue:
- May use a circular doubly-linked list
- EnQueue(x): call insertBack(x)
- DeQueue(x): if queue is not empty, call deleteFront(x)



