洛谷 2540 斗地主增强版
Description
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中,牌的大小关系根据牌的数码表示如下:3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王,而花色并不对牌的大小产生影响。每一局游戏中,一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌,首先打光自己的手牌一方取得游戏的胜利。
现在,牛牛只想知道,对于自己的若干组手牌,分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
需要注意的是,本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。
具体规则如下:
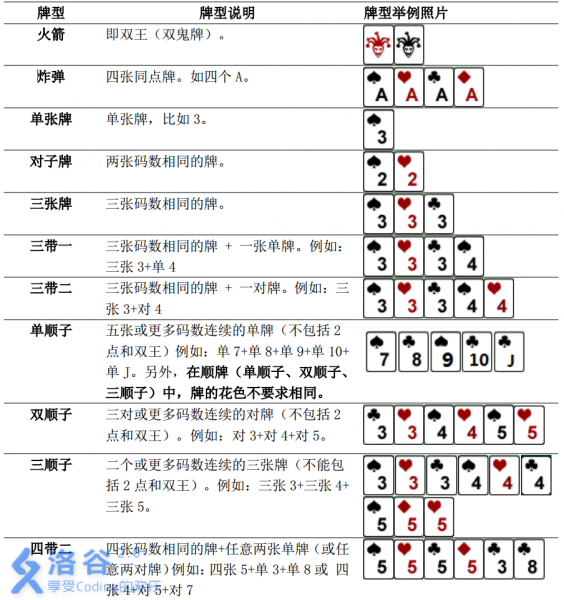
在此题中认为两个王不能组成对子牌
Input
第一行包含用空格隔开的2个正整数T和n,表示手牌的组数以及每组手牌的张数。
接下来T组数据,每组数据n行,每行一个非负整数对aibi表示一张牌,其中ai示牌的数码,bi表示牌的花色,中间用空格隔开。特别的,我们用1来表示数码A,11表示数码J,12表示数码Q,13表示数码K;黑桃、红心、梅花、方片分别用1-4来表示;小王的表示方法为01,大王的表示方法为02。
Output
共T行,每行一个整数,表示打光第i手牌的最少次数。
Sample
1 8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1
3
1 17
12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2
6
Hints
样例1说明
共有1组手牌,包含8张牌:方片7,方片8,黑桃9,方片10,黑桃J,黑桃5,方片A以及黑桃A。可以通过打单顺子(方片7,方片8,黑桃9,方片10,黑桃J),单张牌(黑桃5)以及对子牌(黑桃A以及方片A)在3次内打光。
对于前20个测试点, 我们约定手牌组数T与张数n的规模如下:
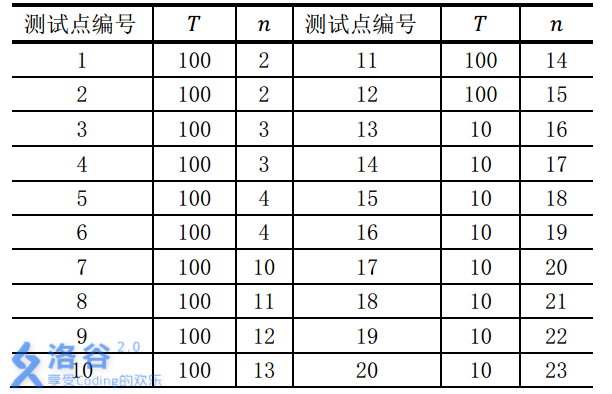
数据不保证所有的手牌都是随机生成的。
好像很早就听说这道神奇的题了,我以为这是一道像模拟的搜索题,就开始傻傻地模拟,但是难过地发现样例就超时了
T了很久,去看了题解,题解是搜索+贪心,打了一会儿,De了很久的bug,终于过了,写题解的时候想不通那个贪心,想了很久,后来终于发现那个贪心有bug
出完顺子以后,不能直接得出答案,因为有些4,3什么的可以拆一下,但是不同情况下的拆法不一样
好像写了4,5个版本,写得要疯掉了●︿●
我发现了自己为什么要T,其实是搜索的时候重复了,确定出牌方法以后,顺序就没有影响了,所以每次枚举的时候不需要把所有出牌方法都搜一遍
Solution
搜索的时候状态不能重复,要按照某一个顺序
✿按照牌的大小顺序搜索
枚举当前这种类型牌以什么形式出
如果是顺子,那么以当前牌为起点,往后找是否能构成顺子
三带二...什么的,可以先不枚举带的那张(对)牌,先记录一下,单牌,对子,三张牌,四张牌各出了多少次,到最后再处理,这样就可以只枚举一种牌一次出几张(优化一下,变成把一个数拆分成什么,因为2总是优于2个1,所以不考虑把2拆成1)
(为4分配2,1,为3分配...什么的,处理的时候,优先为4找两单,两双,一双(相当于两单),然后为3找一单,一双,在答案里减去)
(注意一种牌可能会分几次被出出去,所以如果一次出牌后,还没有出完,下一次要继续搜索这一种牌)
✿按照出牌的顺序出
我没有用这种方法写过,看到有大佬写了,跑得有点慢
每次枚举一种类型的时候,如果互不相关的话,只搜一个(因为答案跟出牌顺序无关),举个栗子,枚举顺子的话,只找到第一个最长的顺子,然后枚举长度,保证与这个顺子相关的顺子都考虑到了,而无关的顺子不需要管,下一次也可以被枚举到
枚举其它牌的方法同上,一个剪枝,如果剩下的单牌,对子什么的可以被出过的三张牌,四张牌带走,就不用往下搜了,直接更新答案
注意细节
比如,大王小王特殊处理
不要把四带两对看成四带一对了
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<queue>
#define inf 100000001
using namespace std;
int pai[21],use[6],res=inf;
int read()
{
int ans=0,f=1;char ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
while(isdigit(ch)) {ans=ans*10+ch-'0';ch=getchar();}
return ans*f;
}
void search(int th,int v)
{
if(th>14)
{
int ne=v,a=use[1],b=use[2],c=use[3],d=use[4];
if(a==2&&b==1&&c==1&&d==1)
{
int debug=1;
}
if(d>=(a>>1))
ne-=(a>>1)<<1,d-=(a>>1),a&=1;
else
ne-=d<<1,a-=d<<1,d=0;
if(d>=(b>>1))
ne-=(b>>1)<<1,d-=(b>>1),b&=1;
else
ne-=d<<1,b-=d<<1,d=0;
if(d>=b)
ne-=b,d-=b,b=0;
if(c>=a)
ne-=a,c-=a,a=0;
else
ne-=c,a-=c,c=0;
if(c>=b)
ne-=b,c-=b,b=0;
else
ne-=c,b-=c,c=0;
res=ne<res? ne:res;
return;
}
if(!pai[th])
{
search(th+1,v);
return;
}
int now=-1;
if(th>=3) //顺子
{
for(int i=th;i<=14;i++)
{
if(pai[i]<3) break;
now=i;
pai[i]-=3;
if(i-th+1>=2)
search(th,v+1);
}
for(int i=th;i<=now;i++)
pai[i]+=3;
now=-1; //////////
for(int i=th;i<=14;i++)
{
if(pai[i]<2) break;
now=i;
pai[i]-=2;
if(i-th+1>=3)
search(th,v+1);
}
for(int i=th;i<=now;i++)
pai[i]+=2;
now=-1;
for(int i=th;i<=14;i++)
{
if(!pai[i]) break;
now=i;
pai[i]--;
if(i-th+1>=5)
search(th,v+1);
}
for(int i=th;i<=now;i++)
pai[i]++;
}
if(pai[th]==4)
{
pai[th]-=4;
use[4]++;search(th+1,v+1);use[4]--;
use[3]++;use[1]++;search(th+1,v+2);use[3]--;use[1]--;
use[2]+=2;search(th+1,v+2);use[2]-=2;
pai[th]+=4;
}
else if(pai[th]==3)
{
pai[th]-=3;
use[3]++;search(th+1,v+1);use[3]--;
use[2]++;use[1]++;search(th+1,v+2);use[2]--;use[1]--; //相当于出了两次,v要+2
pai[th]+=3;
}
else if(pai[th]==2)
{
pai[th]-=2;
use[2]++;search(th+1,v+1);use[2]--;
pai[th]+=2;
}
else if(pai[th]==1)
{
pai[th]--;
use[1]++;search(th+1,v+1);use[1]--;
pai[th]++;
}
}
int main()
{
// freopen("testdata21.in","r",stdin);
// freopen("wo.out","w",stdout);
int t,n,num,co;
t=read();n=read();
for(int j=1;j<=t;j++)
{
if(j==13)
{
int debug=1;
}
res=inf;
memset(pai,0,sizeof(pai)); //傻傻忘清零
memset(use,0,sizeof(use)); //
for(int i=1;i<=n;i++)
{
num=read();co=read();
if(num==1)
pai[14]++;
else if(num==0)
pai[co-1]++;
else
pai[num]++;
}
if(pai[0]&&pai[1])
{
pai[0]--,pai[1]--,search(2,1); //不能放在
pai[0]++,pai[1]++,search(0,0); //
}
else
search(0,0);
printf("%d\n",res);
}
return 0;
}
/*
1 10
1 1
1 1
1 1
1 1
3 1
3 1
3 1
5 1
5 1
7 1
*/


