Roaring bitmaps算法

Roaring bitmaps

最近看一篇文章，里面涉及到使用roaring bitmaps来推送用户广告并通过计算交集来降低用户广告推送次数。本文给出roaring bitmaps的原理和基本用法，后续给出原文的内容。

本文来自：A primer on Roaring bitmaps: what they are and how they work

目录

我从这篇解决大规模留存分析的文章中了解到了Roaring bitmaps，使用Roaring bitmaps而非传统的bitmaps可以将应用使用的内存从~125G下降到300M，节省了99.8%的内存资源。

但这是如何做到的？

下面是两篇与Roaring bitmaps相关的论文：

  1. This one proposes the data structure.
  2. This one introduces a critical optimization.

本文介绍了什么是bitmaps及其用途，什么是Roaring bitmaps以及它是如何解决传统bitmaps中存在的问题的，并一步步揭示Roaring bitmaps的顶层机构及其工作方式。

bitmaps采用了许多算法、技术和启发式方法，这里不作详细介绍，这些细节对理解Roaring bitmaps的基本内部结构和操作并不重要。

什么是bitmaps，bitmaps解决什么问题

Bitmaps 是一个bits位数组，用于存储整数集。

当集合中添加了一个整数N之后，会将第N个bit位设置为1，如下图所示：

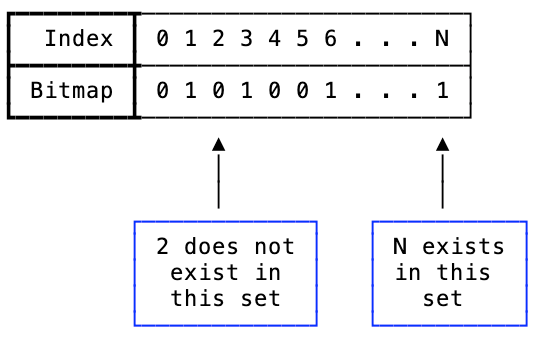
image

图1：bitmaps的运作展示

通过这种存储整数的方式，可以非常快速地使用CPU的位与和位或命令分别计算集合的交集和并集。

事实证明，对于很多查询和数据库应用来说，快速计算集合的交集和并集至关重要。查询和数据库索引中存在各种操作，这些操作可以归结为需要快速计算出交集或并集的两组整数集。

以反向查询索引为例：

  • 假设你已经为数十亿个文档设置了索引，且每个文档都有一个整数id
  • index maps terms表示包含特定词语的一组文档。如pigeon存在于id为{2, 345, 2034, ...}的一组文档中。
  • 使用集合操作来查询多个terms。如为了计算出 carrier AND pigeon，你需要找出包含carrier的文档集合和包含pigeon的文档集合的交集。
  • 使用位操作可以很快地进行集合操作。对于上述例子，只需要执行位与操作就可以找出表示文档id的bit位。

但bitmaps在大规模整数集合场景下的压缩效果不佳。

什么是Roaring bitmaps

roaringbitmap.org中有如下介绍：

Roaring bitmaps是一种压缩的bitmaps，它比bitmaps快百倍。

Roaring bitmaps是一种优化的bitmaps，它和传统的bitmaps一样，都为整数提供了一种集合数据结构。可以插入整数，校验整数的存在性，以及获取两个整数集合的交集和并集等。

相比传统的bitmaps，Roaring bitmaps提供了更好的压缩效果。更重要的是，采用这种方式并不会对性能造成显著的影响。

roaringbitmap.org 中列举了使用Roaring bitmaps 的OLAP数据库和查询系统。

Roaring bitmaps解决了哪些传统bitmaps无法解决的问题?

对于一个稀疏集合，传统的bitmaps的压缩效果较差。

假设一个传统bitmaps为空，添加一个整数8,000,000，此时：

  • 首先分配1,000,000 字节的空间
  • 然后将第8,000,000个bit位设置为1，如下图所示：
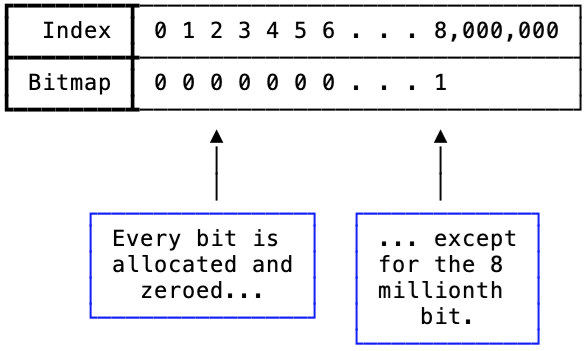
image

图2：如果在一个空的bitmaps中直接分配第800万个bit位，会发生什么。

这种方式会出现如下问题:

  • bitmaps中只设置了一个整数
  • 而一个整数最多需要4个字节
  • 但传统的bitmaps却使用了1M字节的内存，比所需的内存多了6个数量级。

Roaring bitmaps可以在解决该问题的同时保证集合操作的快速性。

先前的很多研究也试图解决bitmaps压缩性较差的问题，并取得了令人印象深刻的结果，但代价是集合操作的性能。

Roaring bitmap是如何工作的

Roaring bitmap使用了多种方式来改善传统bitmaps的性能。

Part 1: Roaring bitmaps 的内存布局

所有32位整数都被划分为连续的块(chunk)。

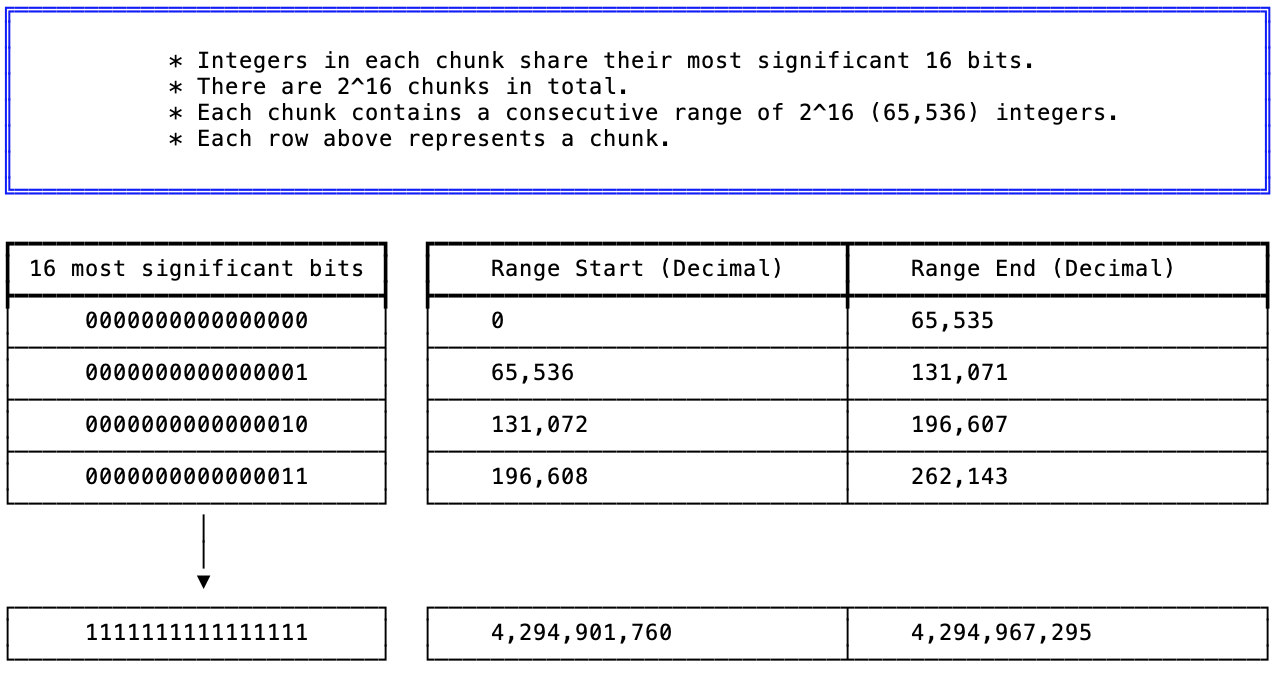
image

图3：如何在Roaring bitmap中将32位的整数空间划分为chunk

Roaring bitmaps最多可以支持2^16个chunks，每个chunk共享相同的16个最高有效位(Msb)，

如上图所示，Roaring bitmaps使用的分区方案可以确保一个整数始终属于2^16(或65536)个连续整数所在的某个chunk。

注意：此外还有64位的Roaring bitmaps实现，本文不对此做深入讨论。

chunks是Roaring bitmaps中对整数的逻辑划分。属于一个chunk的所有整数在物理上都保存在相同的container中。

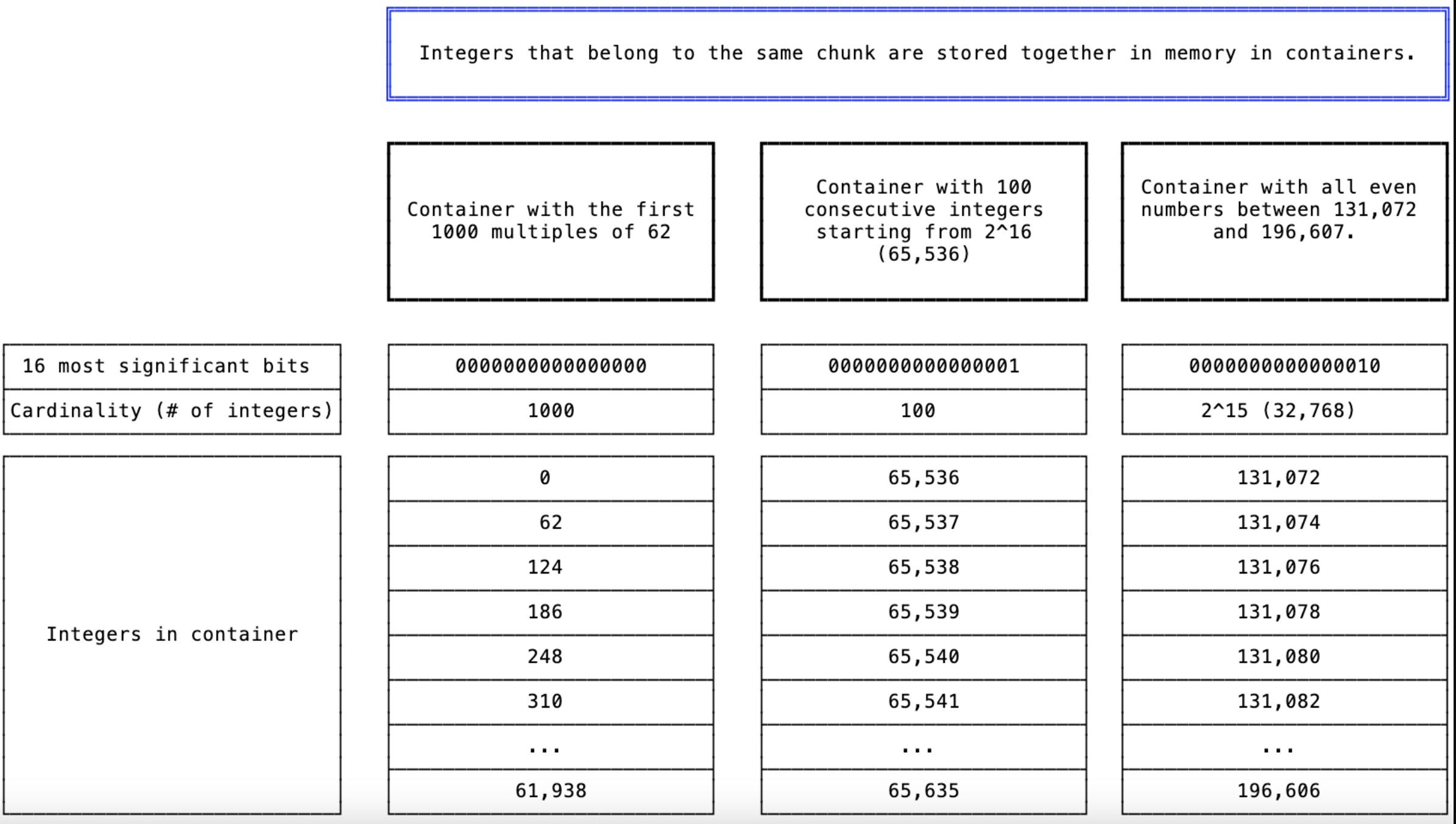
image

图4：来自第一篇Roaring bitmap 论文中的3个containers的例子。

cardinality表示元素个数。

上图展示了3个不同的chunks，对应的3个不同的containers。一个chunk能且只能对应Roaring bitmap中的一个container。

如果将62的倍数的前1000个元素插入到Roaring位图中，那么它们将最终位于图4最左边的容器中。这个容器的cardinality为1000。如果后续插入了整数63，则会落入相同的container中，容器的cardinality将是1001。

后续可以看到，container的cardinality决定了它在内存中的表达方式。

稀疏containers：包含<=4096个整数，它们存储为有序的压缩数组。

图4中最左和中间的两个containers(cardinalities为1000和100)是稀疏的，因此它们将被存储为16位整数的有序压缩数组。

通过压缩，可以将32位稀疏压缩为16位整数，见下图：

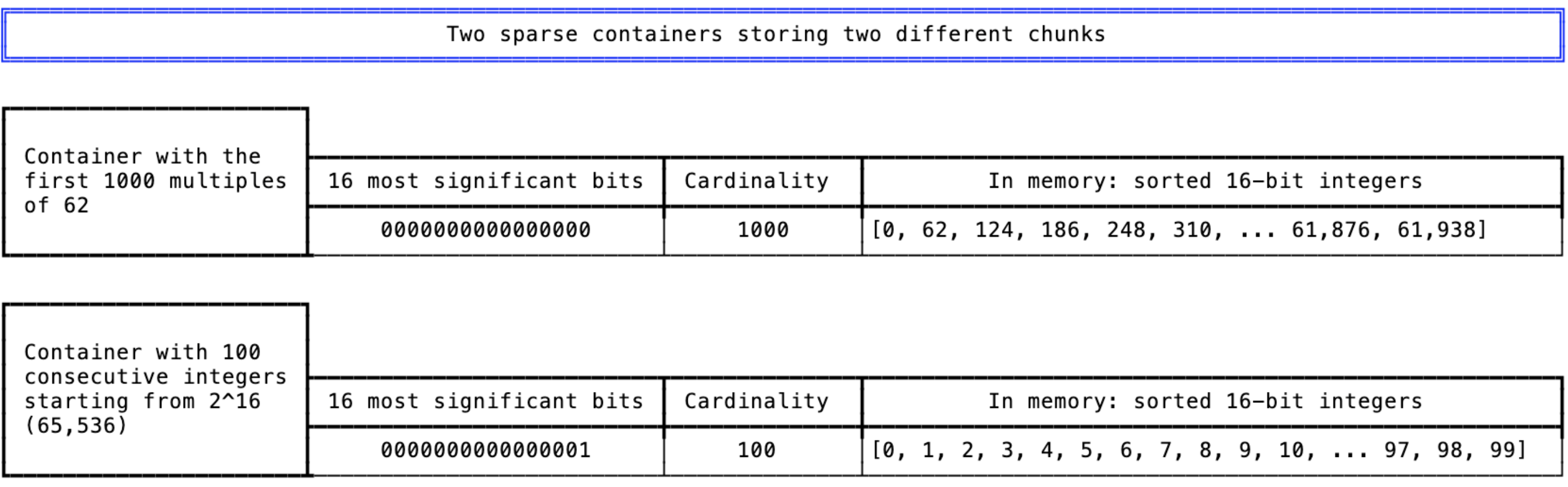
image

图5：图2中的两个稀疏Roaring bitmap container，以及它们如何在内存中存储的示例。

每个container最多可以保存2^16个不同的整数。为了从稀疏container中获取原始的32位整数，可以将16位整数和container的高16位组合起来获取原始整数。

这些数组是动态分配的，因此一个稀疏container中的内存会随着整数的累计而增加。

密集容器：包含>4096个整数，它们被存储为bitmaps。

图4中最右边的container为密集型container(cardinality 为2^15)，因此它会被存储为传统的bitmaps。

image

密集containers为bitmaps，包含2^16位(8KB)的bitmaps，直接分配存储。bitmaps中的第N个bit位对应chunk中的第N个整数。

一级索引指向所有容器，索引存储为有序数组。

一级索引中存储了Roaring bitmap中每个container的高16位，以及指向对应container的指针。

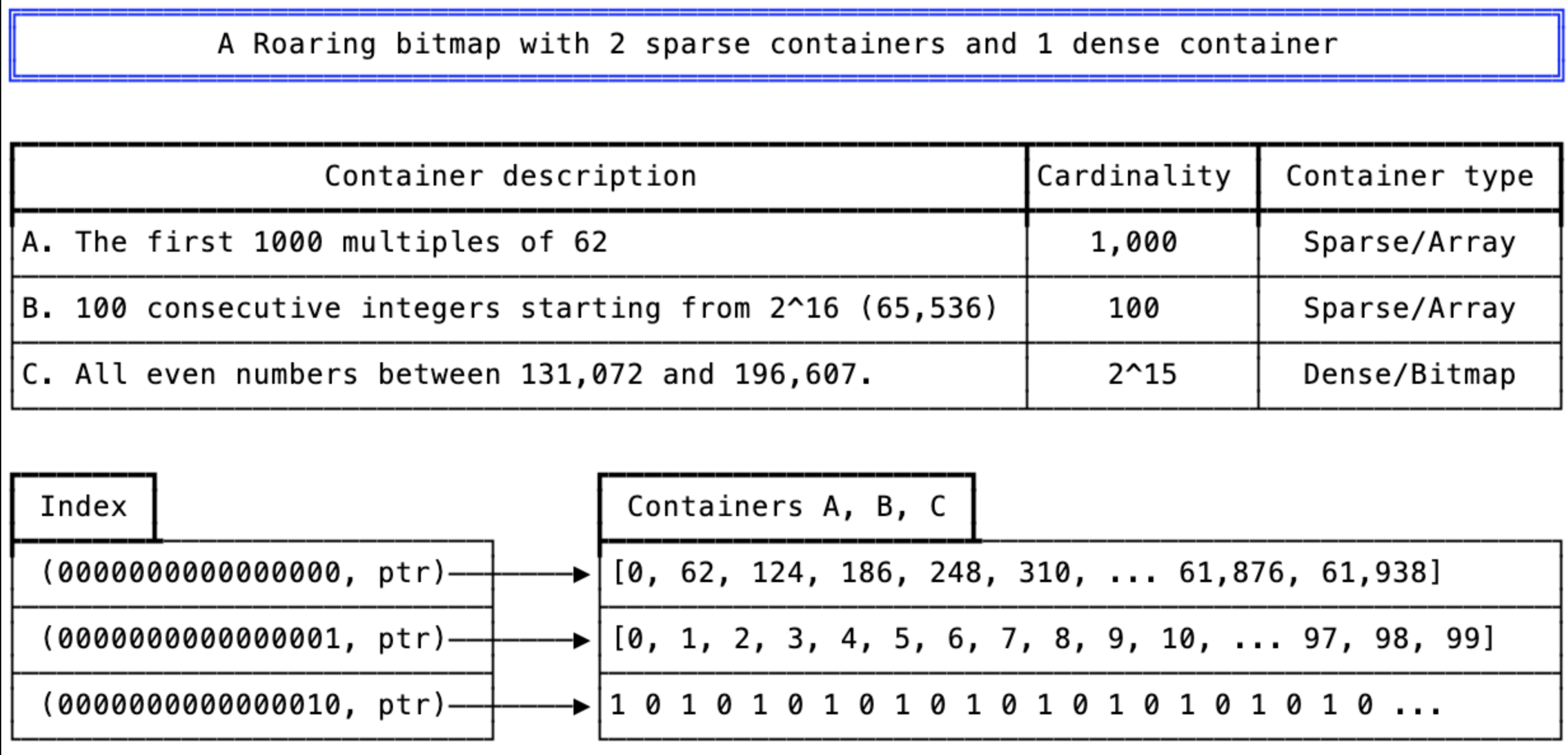
image

图7：一级索引中指向图2、3和4中描述的containern的指针

索引存储为有序数组，并随着Roaring bitmap中containers的增加而动态增长。

Part 2: Roaring bitmaps中的集合操作

整数的插入会因container类型而异，可能会导致container的类型发生变化。

为了插入整数N，首先获取N的高16位(N/2^16)，并在Roaring bitmap中找到N对应的container。

Array container和bitmap container的插入操作不同：

  • Bitmap container：将第N % 2^16个bit位设置为1。注意bitmap是直接分配的。
  • Array container：在有序数组的第N % 2^16个位置插入N。注意数组是动态分配的，随数据的增加而增加。

插入操作可能会改变container的类型，例如一个Array container中有4096个整数，则插入操作会将其转换为一个bitmap container，然后将第N % 2^16个bit位设置为1。

如果一个container不存在，则会首先创建一个新的Array container，然后将其加入Roaring bitmap的一级索引中，最后将N添加到Array container中。

校验数值的存在性会随container类型而异

为了校验是否存在整数N，首先获取N的高16位(N % 2^16)，然后用它在Roaring bitmap中找到对应的container。

如果container不存在，则N也不存在。

Array container和bitmap container的存在性校验方式不同：

  • Bitmap container：校验第N % 2^16个bit位是否为1
  • Array container：使用二分法在有序数组中找到第N % 2^16个位置的值

计算两个Roaring bitmaps的交集。算法会因container类型而异，且container类型也可能发生变化。

为了计算Roaring bitmaps A和B的交集，只需要计算A和B中匹配的containers的交集即可。匹配的container为两个Roaring bitmaps中高16位相同的container，即相同的chunk。

交集运算会随container的类型而异，分为：

  • Bitmap / Bitmap: 计算两个Bitmaps的位与即可。如果cardinality<=4096，则将结果保存在Array container中，否则保存在bitmap container中。
  • Bitmap / Array: 遍历数组，然后在bitmap中校验每个16位整数的存在性。如果整数存在，则将其添加到一个Array container中。注意Bitmap和array container的交集总是会创建出一个array container。
  • Array / Array: 两个array containers的交集总是会生成一个新的array container。交集的运算性能会随着cardinality变化(此篇论文的第5页底部有描述)，可以是简单的合并(和merge sort的方式相同)或快速交集(参见该论文)。

如果一个Roaring bitmap中的某个container没有对应的container，则不会出现在结果中，即交集为空。

Roaring bitmap 的并集。算法会随container类型而异，container类型也可能变化

为了计算Roaring bitmaps A和B的并集。需要计算A和B中匹配containers的并集。

并集运算可能会因container类型而异，有如下几种：

  • Bitmap / Bitmap: 计算两个bitmaps的位或。两个bitmap container的并集总是会创建另一个bitmap container。
  • Bitmap / Array: 复制bitmap，并在该bitmap中为array container中的所有整数设置bit位。bitmap和array container的并集总是会创建另一个bitmap container。
  • Array / Array: 如果两个array container的cardinalities总数<=4096，则生成的container会是一个array container。这种情况下，会将两个arrays中的所有整数添加到一个新的array container中。否则会假设生成的container是一个bitmap：创建一个新的bitmap container，然后在该bitmap中为两个array containers中的整数设置bit位。如果生成的container的cardinality<=4096，则将该bitmap container转换为一个array container。

最后，将A和B中没有匹配container的所有containers添加到结果中。

Part 3：第三种也是最后一种container类型——"run" container——如何优化大量连续的整数

part 1和2中涵盖了Roaring bitmaps的大分部内部结构和操作。最后讨论一下Roaring bitmaps的第二篇论文中的一个重要优化。

run container为使用两个16位整数表示的连续整数：run开始和run长度。

第二篇论文的第3页有如下表述：

新容器在概念上很简单：给定一个run(例如[10,1000])，我们存储起点(10)及其长度减1(990)。然后将起点和长度成对打包，开始值和长度值都为16位整数。

这种技术称为run-length编码。Run-length可以有效压缩bitmaps，但在很多场景下，却降低了set操作的性能。

当客户端调用runOptimize函数时，run container是显式形成的，而在某些情况下，当向Roaring bitmap中添加了大范围数值时，则是隐式形成的。

与稀疏和密集container不同，run container通常不会自动形成。

  1. 客户端可以调用runOptimize来优化Roaring bitmap中的大量连续整数，这种情况下，run container可能会替代现有的array 或 bitmap container。
  2. Roaring bitmap提供了一个添加连续数值的操作，这种情况下，可能会形成run container。

该篇论文没有具体规定如何以及合时会发生第二种场景。可能场景是，为一个还没有container的chunk添加了一段连续的值，那么此时创建一个run container(而不是array或bitmap container)可能更有意义。

runOptimize仅在run container小于要替换的container时才会创建该container。

runOptimize首先会计算一个container中的连续值的数量。然后再决定是否需要创建一个run container：run container必须要小于等同的array或bitmap container。

在第2篇论文的第6,7页描述了一种用于计算连续值数量的算法：

run container的添加为所有集合操作引入了新的算法。

Roaring bitmaps论文中并没有描述run container的插入和校验整数存在性的算法：这些操作相对简单。

但是，添加run container需要为如下组合实现高性能并集和交集算法：

  • Run / Run
  • Run / Array
  • Run / Bitmap

这里不再作深入讨论，这些算法也不会太复杂(参见该论文的第10页)。

Roaring bitmaps使用了多种算法和技术，与其他bitmaps实现相比，可以实现更好的压缩效果和更快的性能。

Roaring bitmaps的实现很有挑战性，但它的表现却很好，尤其是在OLAP工作负载中使用时。创建者设法根除常见的多种场景中存在的低效率问题——稀疏数据、密集数据、大量连续的数据——并且同时解决了所有这些问题。

第3篇论文描述了创建者使用C语言编写的一个实现，该实现利用了他们使用SIMD(单指令多数据)指令设计的矢量化算法。这里提供了该实现、CRoaring以及其他多种语言的实现。它们被用于主流的柱状数据库和搜索应用程序，并得到了积极的维护、改进和优化。

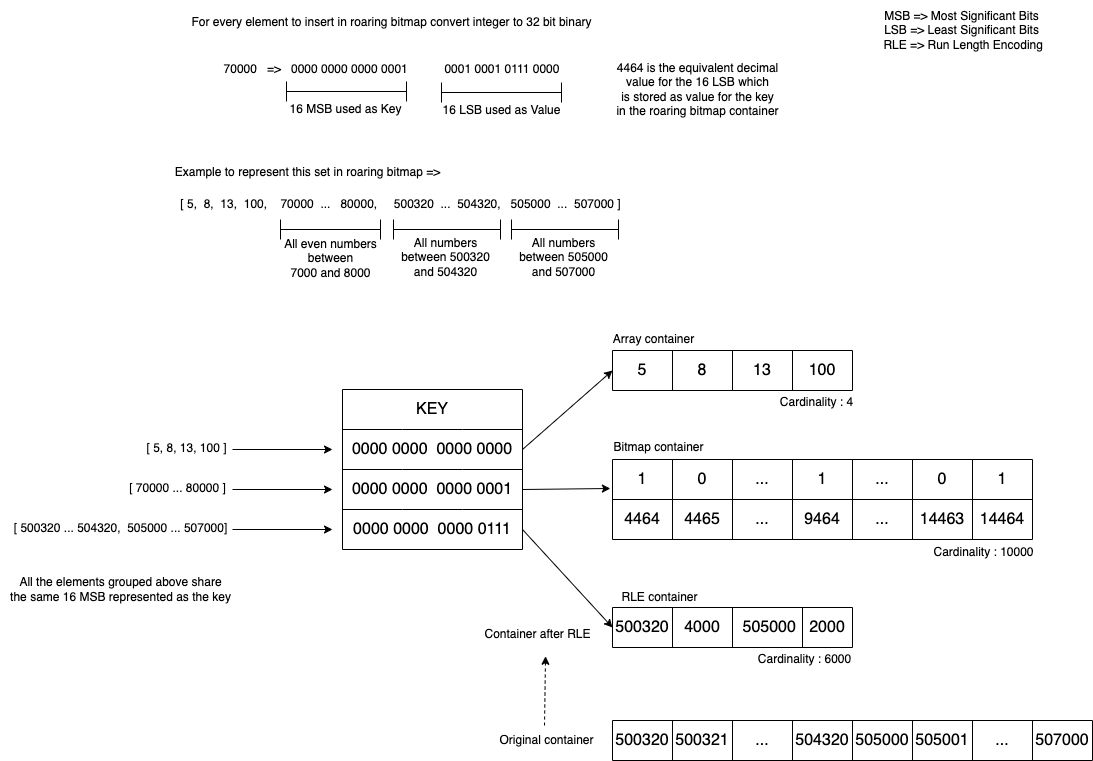
下面这张图给出了3种container的用法(RLE(Run-Length Encoding)即run container)

image

Golang的roaring bitmaps

Roaring bitmaps可以实现整数集合的交集和并集运算，并在保证数据压缩效果的同时同时保证了运算的高效性。

这里给出了golang版本的实现。分为32位和64位两种。需要注意的是bitmaps并不是goroutines安全的。下面32位的Roaring bitmaps为例看下bitmap container和array container是如何添加数据的。

在上文中有讲，当container为bitmaps类型时，会直接分配存储，从下面bitmap container的初始化中可以看到，其初始化会直接分配65535 bit位的存储空间。当bitmap存储满后，会被压缩为run container。

func newBitmapContainer() *bitmapContainer {
	p := new(bitmapContainer)
	size := (1 << 16) / 64
	p.bitmap = make([]uint64, size, size)
	return p
}

而array container中主要用于存储稀疏数值。下面是在array container中添加数值的函数。可以看到array container并不是预先分配的，它随添加的数值的增加而增加。


func (ac *arrayContainer) iaddReturnMinimized(x uint16) container {
	// Special case adding to the end of the container.
	l := len(ac.content)
  // arrayDefaultMaxSize为4096。下面表示如果当前container中的数值总数没有超过最大值，
  // 且要添加的值x大于有序数组的最后一个时，只需要将x追加到有序数组的最后一个即可
	if l > 0 && l < arrayDefaultMaxSize && ac.content[l-1] < x {
		ac.content = append(ac.content, x)
		return ac
	}

  // 使用二分法找到x或插入x的位置
	loc := binarySearch(ac.content, x)

  // 如果loc<0表示没有在container中找到x，如果当前container中的数值总数为arrayDefaultMaxSize，
  // 则需要转换为bitmap container，然后再添加x。
  // 否则根据找到的位置loc，再在array container中插入x
	if loc < 0 {
		if len(ac.content) >= arrayDefaultMaxSize {
			a := ac.toBitmapContainer()
			a.iadd(x)
			return a
		}
		s := ac.content
		i := -loc - 1
		s = append(s, 0)
		copy(s[i+1:], s[i:])
		s[i] = x
		ac.content = s
	}
	return ac
}
posted @ 2023-12-25 19:42  charlieroro  阅读(641)  评论(0)  编辑  收藏  举报