PRelu和一些激活函数
PRelu可以参考这篇文章:
https://www.cnblogs.com/catpainter/p/8406285.html
PReLU全名Parametric Rectified Linear Unit. PReLU-nets在ImageNet 2012分类数据集top-5上取得了4.94%的错误率,首次超越了人工分类的错误率(5.1%)。PReLU增加的计算量和过拟合的风险几乎为零。考虑了非线性因素的健壮初始化方法使得该方法可以训练很深很深的修正模型(rectified model)来研究更深更大的网络结构。
ReLU和PReLU图像:

PReLU的数学表达式(i代表不同的通道,即每一个通道都有参数不相同的PReLU函数):
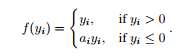
ai被初始化为0.25。
神经网络为什么需要非线性激活函数?
非线性函数是指的一阶导数不为常数的函数
线性函数的组合还是线性函数,所以网络再深,最后输出的还是线性函数。所以用非线性激活函数,神经网络理论上可以逼近任意函数。
激活函数在神经网络中的应用,除了引入非线性表达能力,其在提高模型鲁棒性、缓解梯度消失问题、将特征输入映射到新的特征空间以及加速模型收敛等方面都有不同程度的改善作用
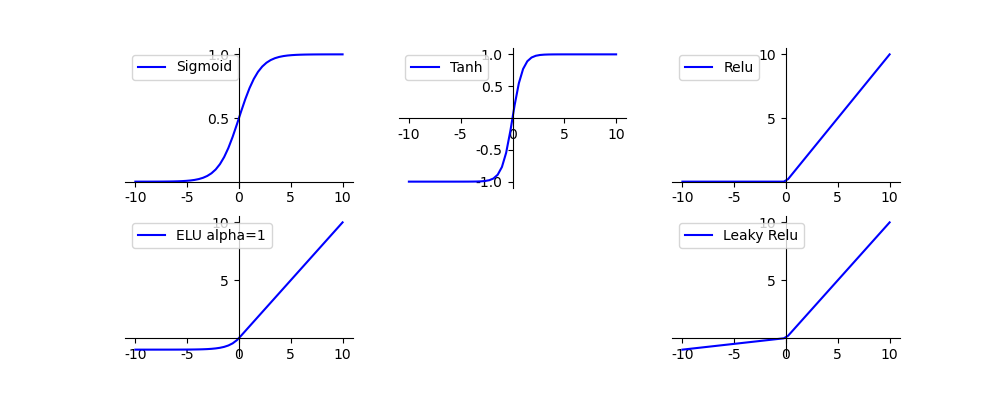
常见的激活函数主要包括如下几种:sigmoid函数、tanh函数、Relu函数、Leaky Relu函数、ELU函数。
以下参考这篇文章:
https://www.cnblogs.com/Joejwu/p/Joejwu_blog210618.html
《常用激活函数:Sigmoid、Tanh、Relu、Leaky Relu、ELU优缺点总结》
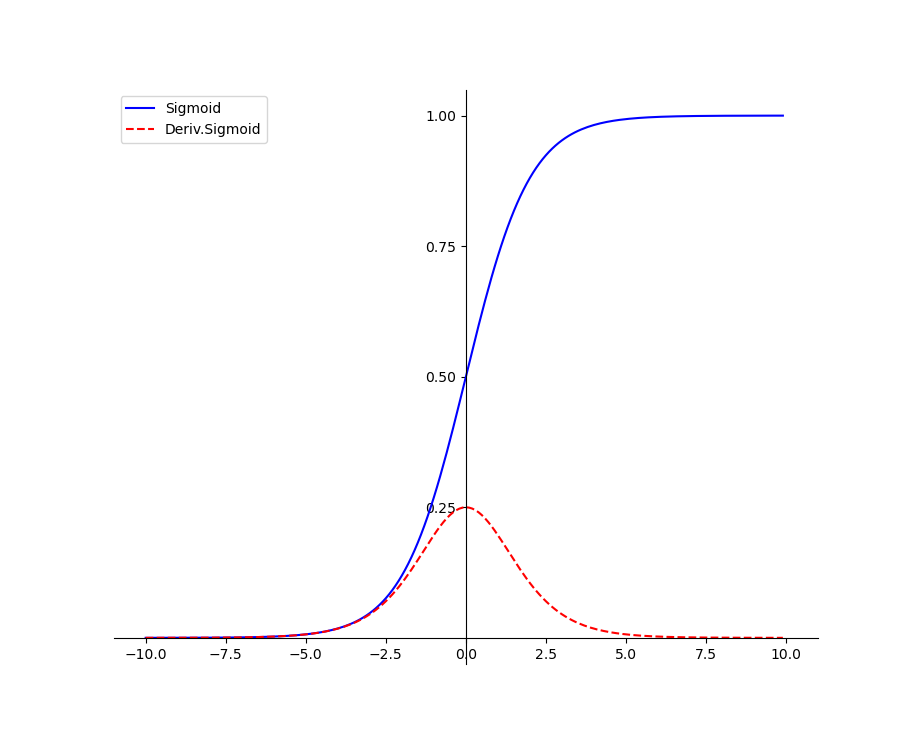
Sigmoid函数
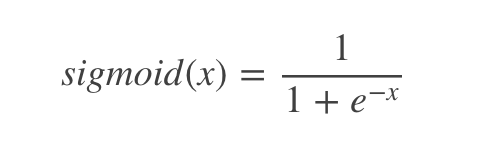
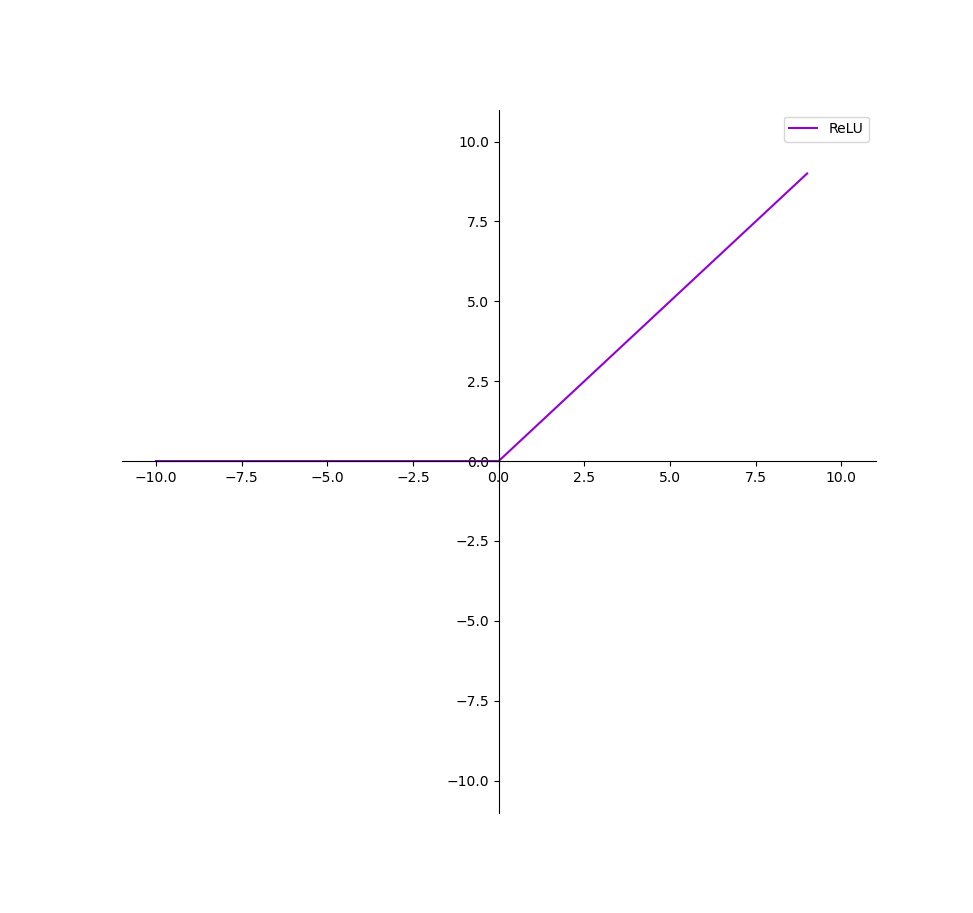
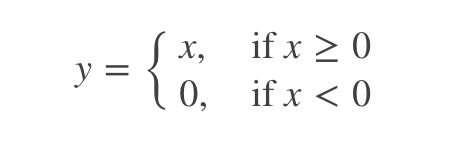
上图即为Relu函数的曲线图,可见在输入为负值时,输出均为0值,在输入大于0的区间,输出y=x,可见该函数并非全区间可导的函数;其优缺点总结如下:
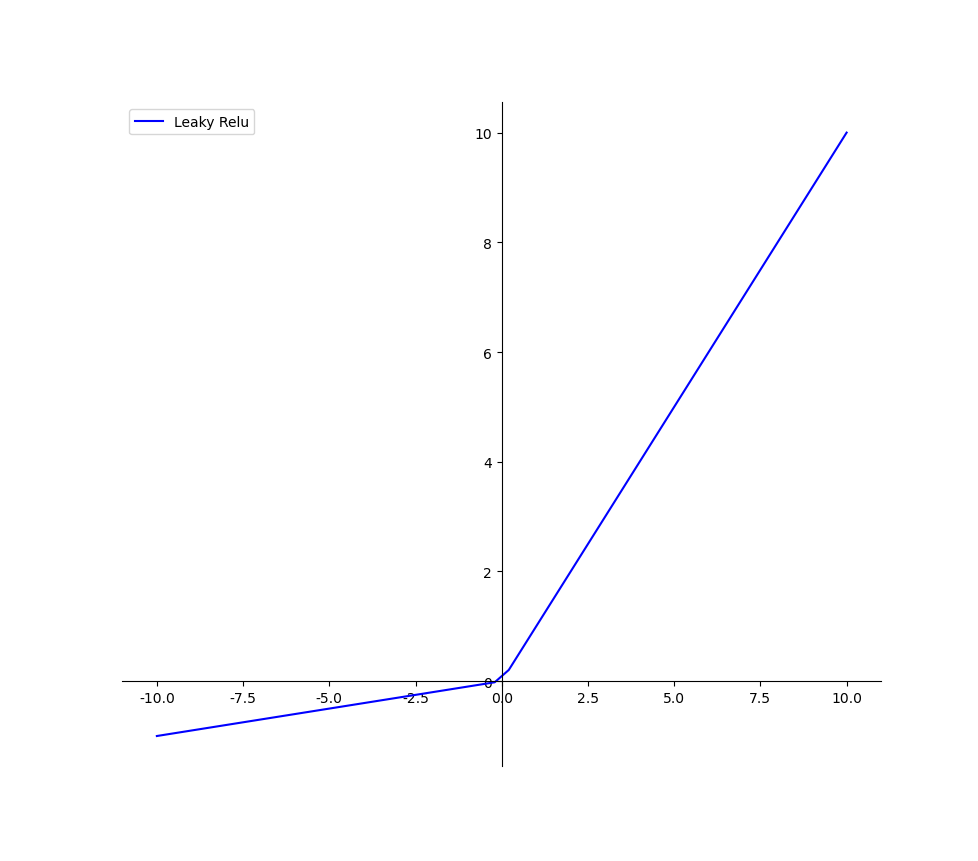
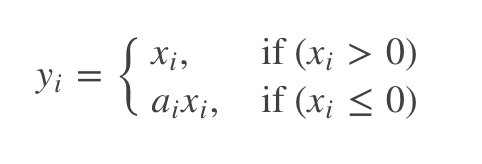 (a固定的话就是LRelu,不固定的话就是PRelu)
(a固定的话就是LRelu,不固定的话就是PRelu)
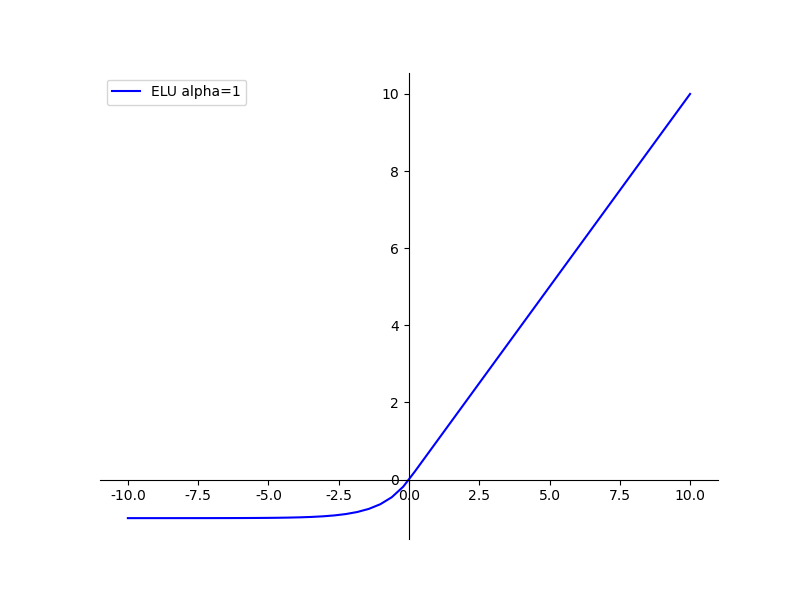
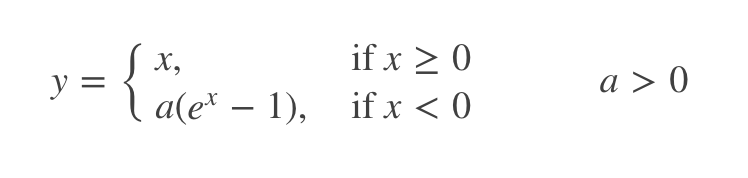
图中所示即为ELU函数,其也是Relu函数的一种变体,x大于0时,y=x,x小于等于0时,y=α(exp(x)-1),可看作介于Relu与Leaky Relu之间的函数;其优缺点总结如下:
以下参考这篇文章:
https://www.cnblogs.com/makefile/p/activation-function.html
Maxout

优点:
- Maxout的拟合能力非常强,可以拟合任意的凸函数。
- Maxout具有ReLU的所有优点,线性、不饱和性。
- 同时没有ReLU的一些缺点。如:神经元的死亡。
缺点:
从上面的激活函数公式中可以看出,每个神经元中有两组(w,b)参数,那么参数量就增加了一倍,这就导致了整体参数的数量激增。
与常规激活函数不同的是,它是一个可学习的分段线性函数.
然而任何一个凸函数,都可以由线性分段函数进行逼近近似。其实我们可以把以前所学到的激活函数:ReLU、abs激活函数,看成是分成两段的线性函数,如下示意图所示:

实验结果表明Maxout与Dropout组合使用可以发挥比较好的效果。
前边的两种ReLU便是两种Maxout,函数图像为两条直线的拼接。
梯度消失/爆炸原因及解决办法
原因,浅层的梯度计算需要后面各层的权重及激活函数导数的乘积,因此可能出现前层比后层的学习率小(vanishing gradient)或大(exploding)的问题,所以具有不稳定性.
怎么解决,需要考虑几个方面:
- 权重初始化
使用合适的方式初始化权重, 如ReLU使用MSRA的初始化方式, tanh使用xavier初始化方式. - 激活函数选择
激活函数要选择ReLU等梯度累乘稳定的. - 学习率
一种训练优化方式是对输入做白化操作(包括正规化和去相关), 目的是可以选择更大的学习率. 现代深度学习网络中常使用Batch Normalization(包括正规化步骤,但不含去相关). (All you need is a good init. If you can't find the good init, use Batch Normalization.)
梯度爆炸
由于sigmoid,ReLU等函数的梯度都在[0,1]以内,所以不会引发梯度爆炸问题。 而梯度爆炸需要采用梯度裁剪、BN、设置较小学习率等方式解决。
激活函数选择
- 首先尝试ReLU,速度快,但要注意训练的状态.
- 如果ReLU效果欠佳,尝试Leaky ReLU或Maxout等变种。
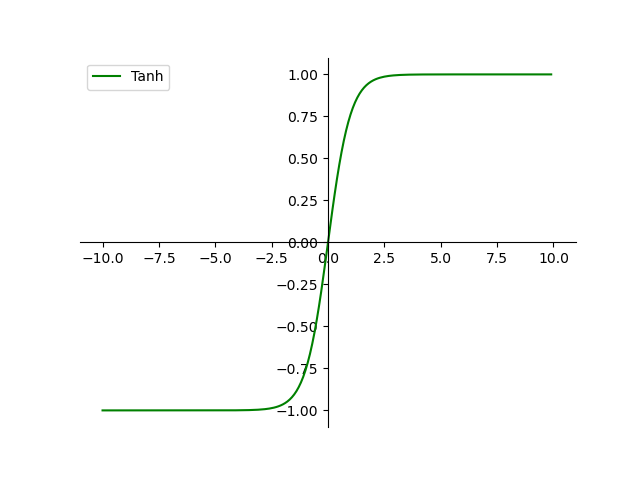
- 尝试tanh正切函数(以零点为中心,零点处梯度为1)
- sigmoid/tanh在RNN(LSTM、注意力机制等)结构中有所应用,作为门控或者概率值.
- 在浅层神经网络中,如不超过4层的,可选择使用多种激励函数,没有太大的影响。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号