优化算法的一些摘要

参考这篇文章：

https://zhuanlan.zhihu.com/p/32230623

 

深度学习优化算法经历了 SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam 这样的发展历程。

我们换一个思路，用一个框架来梳理所有的优化算法，做一个更加高屋建瓴的对比。

 

 

SGD

SGD没有动量的概念，也就是说

代入步骤3，可以看到下降梯度就是最简单的

SGD最大的缺点是下降速度慢，而且可能会在沟壑的两边持续震荡，停留在一个局部最优点。

 

 

SGD with Momentum

t时刻的下降方向，不仅由当前点的梯度方向决定，而且由此前累积的下降方向决定。  的经验值为0.9，这就意味着下降方向主要是此前累积的下降方向，并略微偏向当前时刻的下降方向。想象高速公路上汽车转弯，在高速向前的同时略微偏向，急转弯可是要出事的。

 

SGD with Nesterov Acceleration

SGD 还有一个问题是困在局部最优的沟壑里面震荡。

NAG全称Nesterov Accelerated Gradient

NAG在步骤1，不计算当前位置的梯度方向，而是计算如果按照累积动量走了一步，那个时候的下降方向。

 

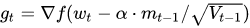
然后用下一个点的梯度方向，与历史累积动量相结合，计算步骤2中当前时刻的累积动量。

 

AdaGrad

此前我们都没有用到二阶动量。二阶动量的出现，才意味着“自适应学习率”优化算法时代的到来。

SGD及其变种以同样的学习率更新每个参数，但深度神经网络往往包含大量的参数。

 

对于经常更新的参数，我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；对于偶尔更新的参数，我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。

 

那就是二阶动量——该维度上，迄今为止所有梯度值的平方和：

我们再回顾一下步骤3中的下降梯度：

可以看出，此时实质上的学习率由  变成了  。 一般为了避免分母为0，会在分母上加一个小的平滑项。因此 是恒大于0的，而且参数更新越频繁，二阶动量越大，学习率就越小。

 

但也存在一些问题：因为 是单调递增的，会使得学习率单调递减至0，可能会使得训练过程提前结束，即便后续还有数据也无法学到必要的知识。

 

AdaDelta / RMSProp

 

由于AdaGrad单调递减的学习率变化过于激进，我们考虑一个改变二阶动量计算方法的策略：不累积全部历史梯度，而只关注过去一段时间窗口的下降梯度。这也就是AdaDelta名称中Delta的来历。

 

这就避免了二阶动量持续累积、导致训练过程提前结束的问题了。

 

Adam

SGD-M在SGD基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来，就是Adam了——Adaptive + Momentum。

SGD的一阶动量：

加上AdaDelta的二阶动量：

 

优化算法里最常见的两个超参数  就都在这里了，前者控制一阶动量，后者控制二阶动量。

 

Nadam

最后是Nadam。我们说Adam是集大成者，但它居然遗漏了Nesterov，这还能忍？必须给它加上。

这就是Nesterov + Adam = Nadam了。

 

而Adam和Nadam的问题，可以看后面这篇文章：

https://zhuanlan.zhihu.com/p/32262540