【排序算法】堆排序的推导及实现
HeapSort 是一种基本算法,其精确的性能特征已被证明难以分析。很容易证明,在最坏的情况下,当对 N 个不同元素的随机文件进行排序时,算法在算法过程中移动的键数为
NlgN + O(N),并且长期以来人们一直猜测平均性能为相同。尽管该算法是被广泛使用的经典方法,但仍未发现一般情况甚至最佳情况的具体结果。
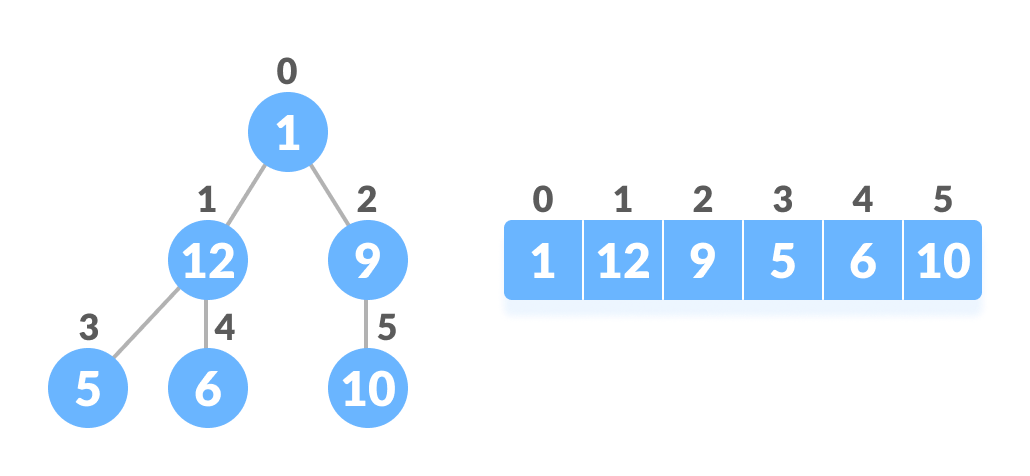
数组索引和树元素之间的关系
完全二叉树具有一个特殊的属性,我们可以用来查找任何节点的子节点和父节点。
如果数组中任何元素的索引为 i,索引中的元素 2i+1 将成为左叶子节点,2i+2 索引中的元素将成为右叶子节点。了解数组索引到树位置的这种映射关系,对于堆数据结构如何工作及如何实现堆排序至关重要。
什么是堆数据结构?
堆是一种特殊的基于树的数据结构。在其他一些场合中,“堆”是指能够分配可变大小的结点的一段较大的内存。示例中堆用于表示数值,但实际上堆中的元素可以是任何数据类型。如果满足以下条件,则可以说二叉树遵循堆数据结构:
- 它是一个完全二叉树;
- 树中的所有节点都遵循其大于子节点的属性,即每个结点的值都大于或等于其左右叶子结点的值,这样的堆称为最大堆。相反,如果所有节点都小于其子节点,则称为最小堆。
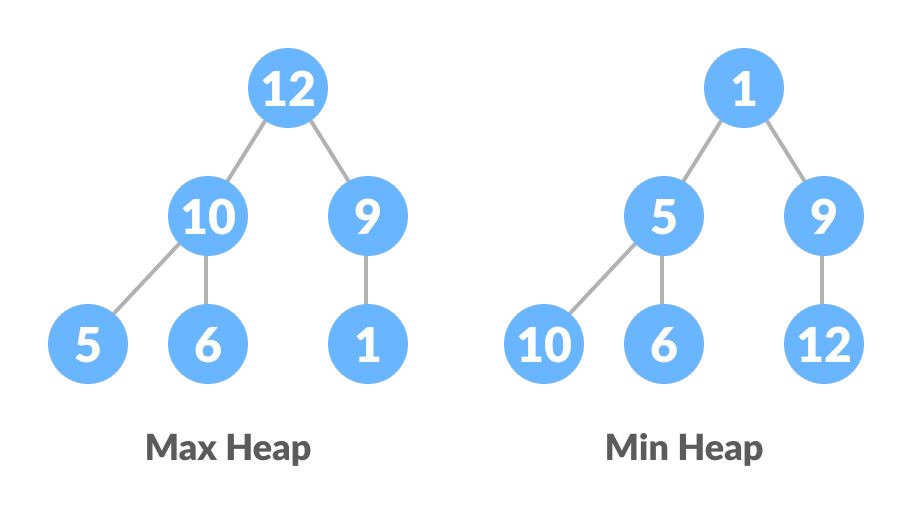
由于形状性质是通过表示方法来保证的,我们约定“堆”这个词意味着任何节点的值都大于或等于其夫结点的值。更准确的说:大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
非叶子节点推导
- 从二叉树由下而上看,除了根节点每个节点都有一个入度,所以一个 n 个节点二叉树的度
n-1; - 设 n 个节点中有 x 个非叶子节点和 y 个叶子节点,
x+y =n,从上往下看,所有的非叶子节点都有两个出度,叶子节点没有,则2x = n-1 = x+y-1 => x=y-1; - 从上面公式可知非叶子节点比叶子节点少一个,而 int 型在在进行除法时会自动去除小数点,所以
arr.leng /2就类似于(n-1)/2。因为是数组下标,都需要减一,所以int i = arr.length/2 -1;
二叉树到堆的实现
从完全二叉树开始,我们可以通过在堆的所有非叶节点上运行一个定义为 heapify 的函数,将其修改为最大堆。从最简单的一颗树来看:
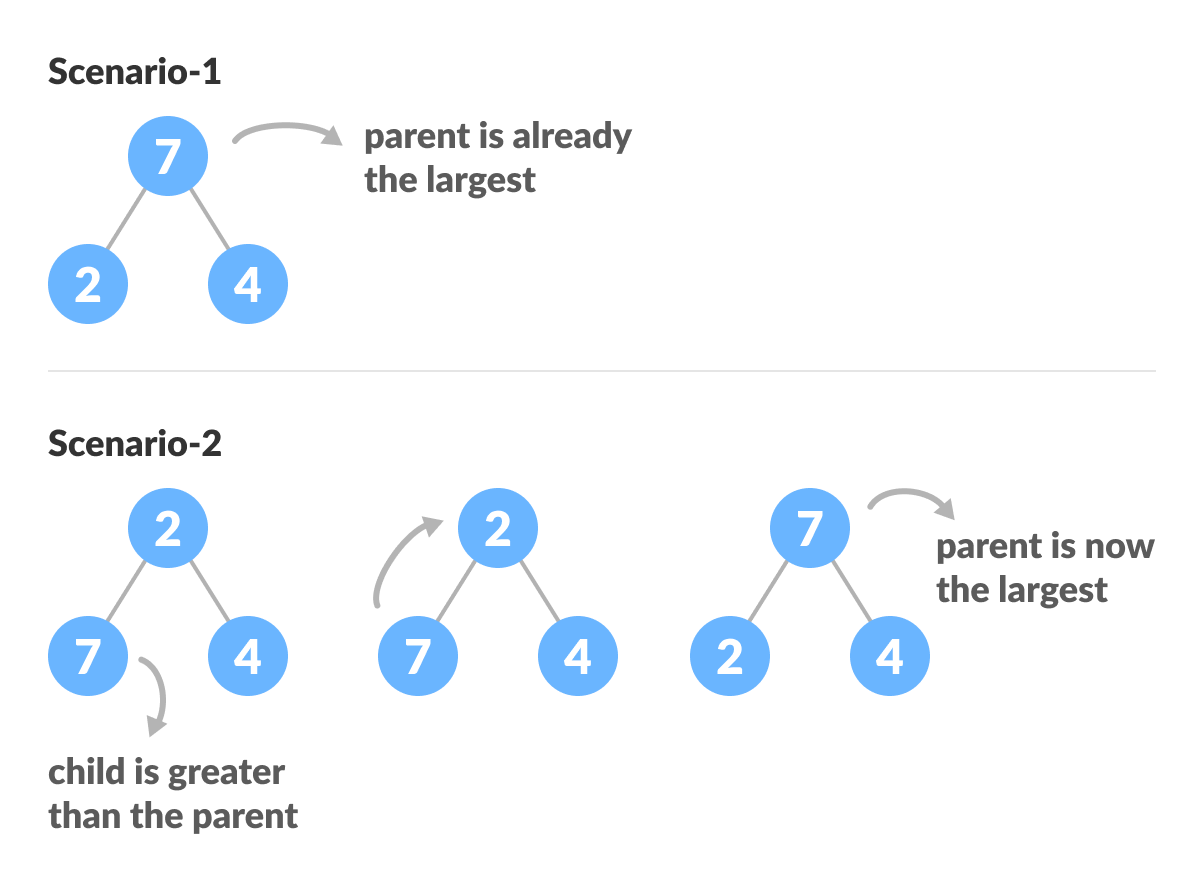
上面的示例显示了两种情况:一种是根是最大的元素,而我们不需要做任何事情。另一个根中有一个较大的元素,我们需要交换以维护 max-heap 属性。我们考虑另一个场景,其中完全二叉树存在多个级别。顶部元素不是大顶堆,但是所有子树都是大顶堆。为了保持整个树的 max-heap 属性,我们需要将子树对应的节点下沉直到它到达正确的位置。
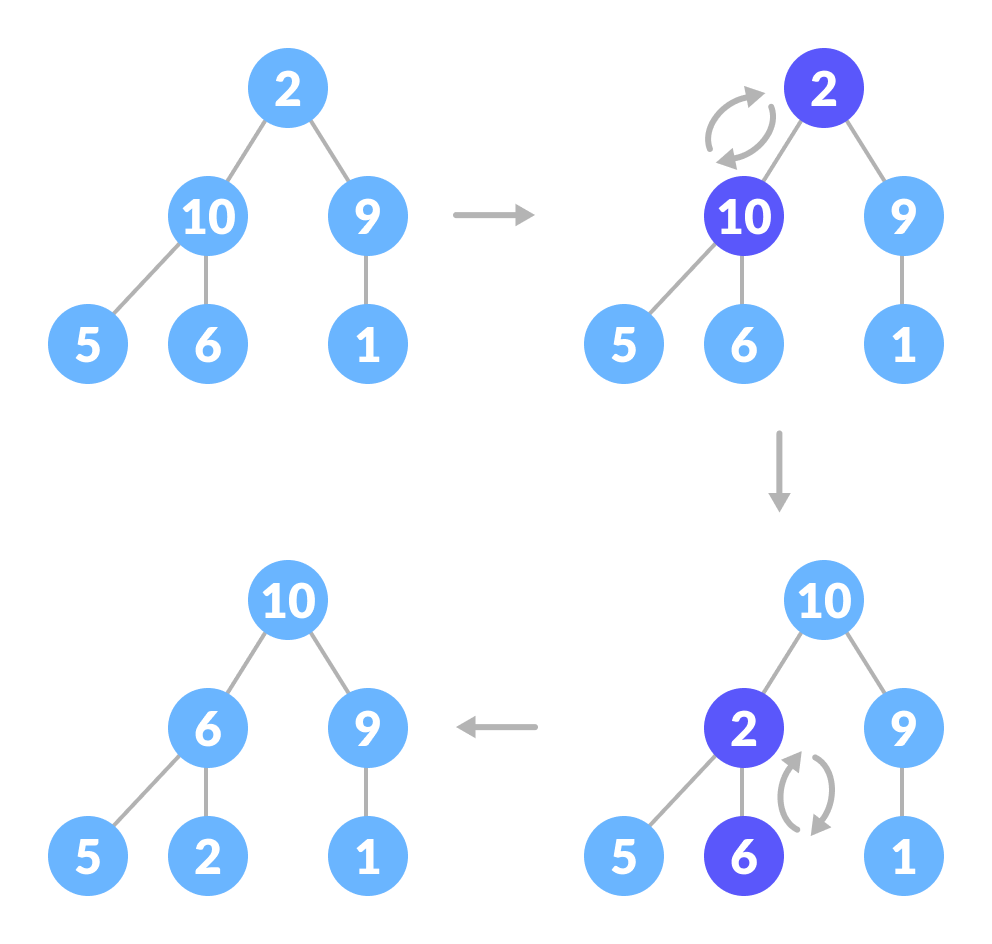
因此,要在两个子树都是 max-heap 的树中维护 max-heap 属性,我们需要在根节点上重复运行 heapify,直到它大于其子节点或成为叶节点为止。
我们可以将这两个条件组合在一个heapify函数中:
void heapify(int arr[], int n, int i) {
// Find largest among root, left child and right child
int largest = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < n && arr[left] > arr[largest])
largest = left;
if (right < n && arr[right] > arr[largest])
largest = right;
// Swap and continue heapifying if root is not largest
if (largest != i) {
swap(&arr[i], &arr[largest]);
heapify(arr, n, largest);
}
}
heapify 函数适用于基本情况和任何大小的树。因此,只要子树是大顶堆,我们就可以将根元素移动到正确的位置以保持任何树大小的大顶堆状态。
构建大(小)顶堆
要从任何树构建最大堆,我们可以从下至上开始对每个子树进行筛选,并在将函数应用于包括根元素的所有元素后以大顶堆结束。
对于完全二叉树,非叶子节点的第一个索引为 n/2 - 1。之后的所有其他节点都是叶节点,因此不需要做处理。
因此,我们可以构建一个最大堆
// Build heap (rearrange array)
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
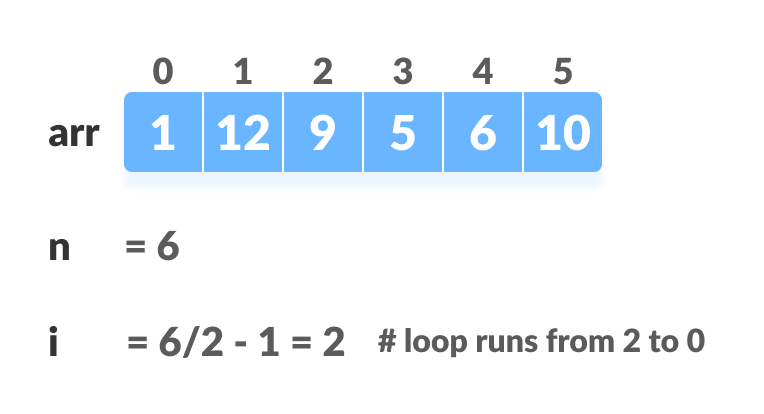
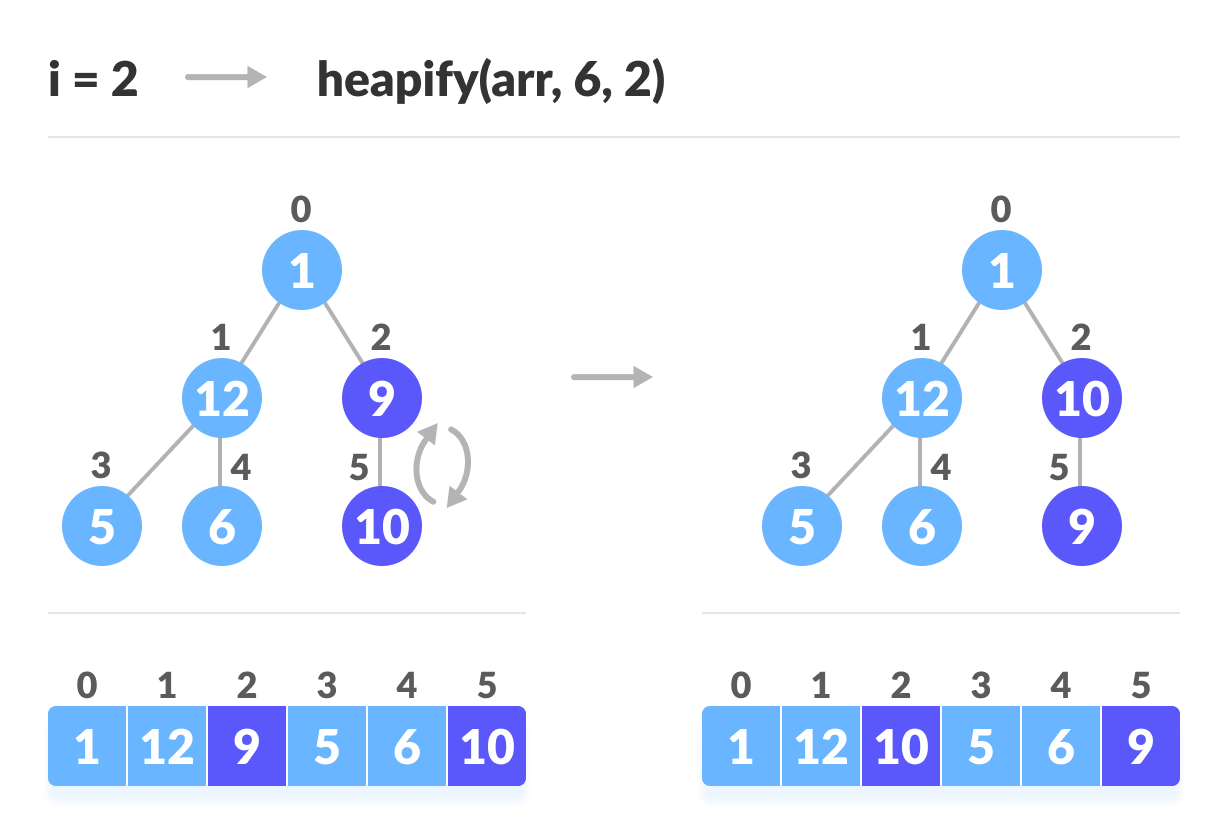
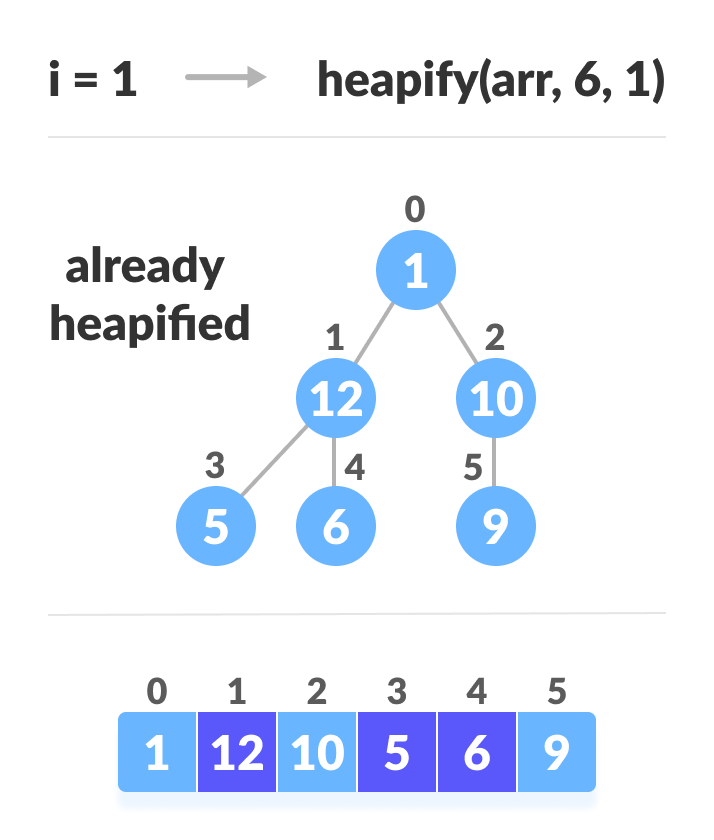
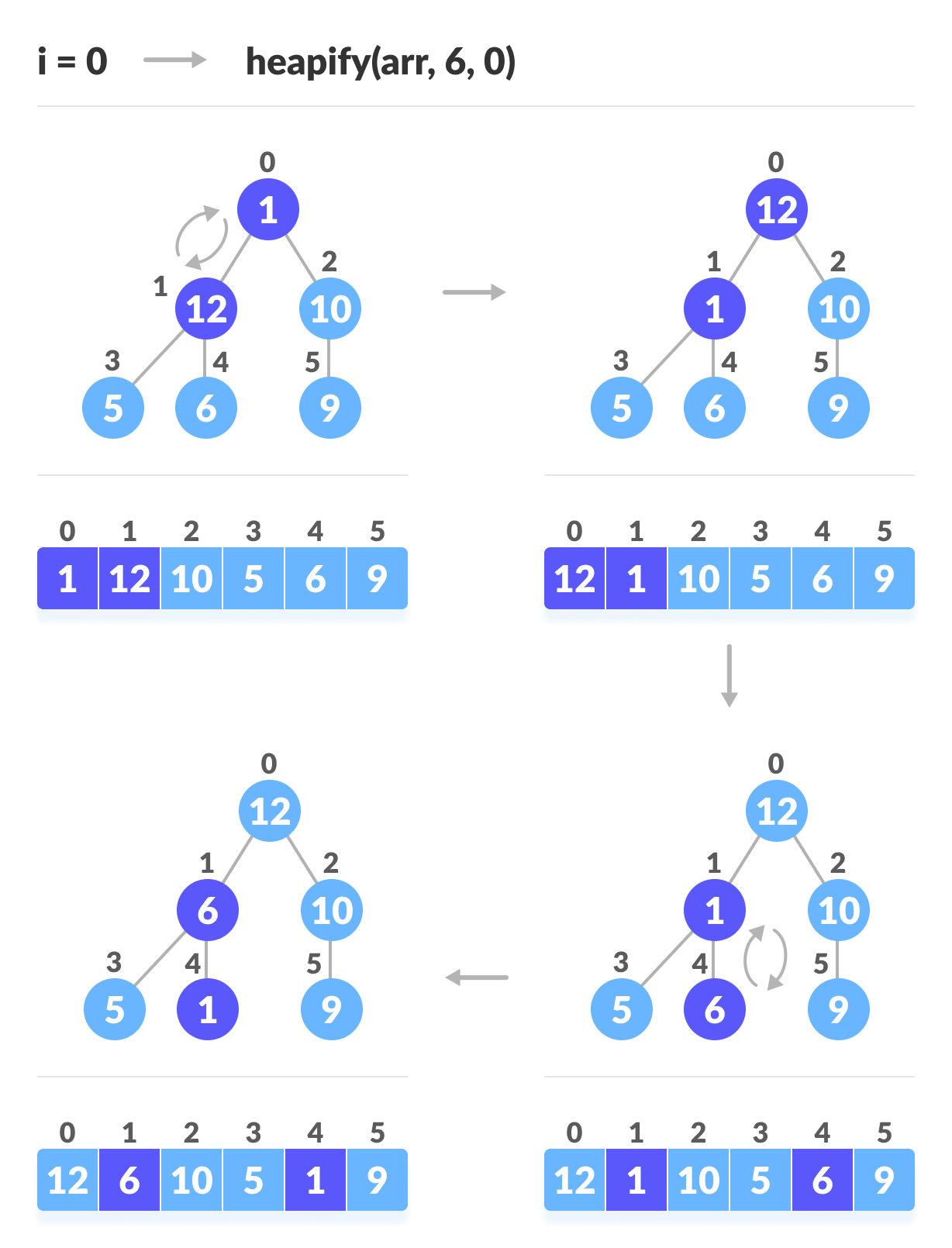
如上图所示,我们首先构建最小的最小树,然后逐渐向上移动直到到达根元素。
堆排序如何工作
- 由于树满足 Max-Heap 属性,因此最大的项存储在根节点上。
- 交换:删除根元素,并将其放在数组的末尾(第 n 个位置)。将树的最后一项(堆)放在空白处。
- 删除:将堆大小减小1。
- 构建:再次构建根元素,以便我们在根上拥有最大的元素。
- 重复该过程,直到对列表中的所有项目进行排序为止。
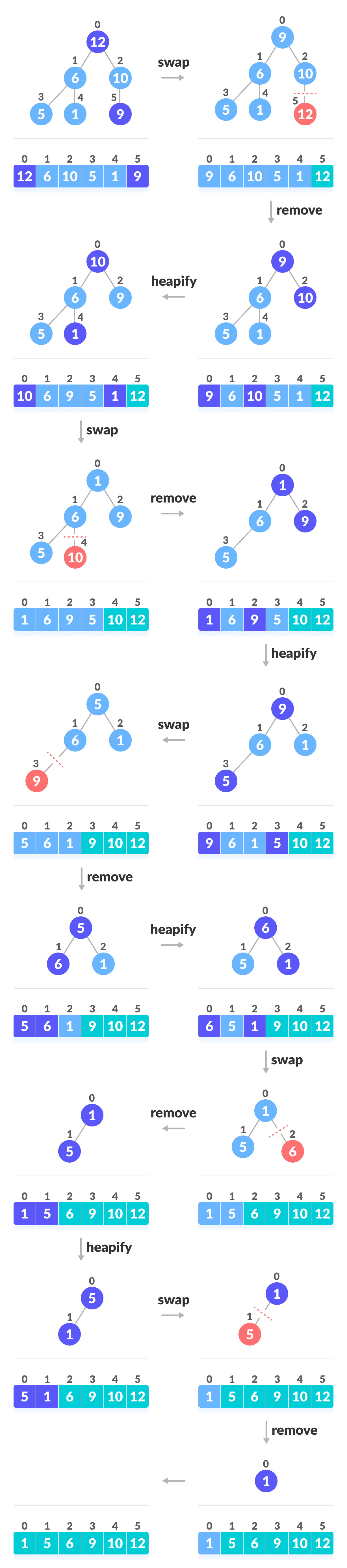
下面的代码显示了该操作。
// Heap sort
for (int i = n - 1; i >= 0; i--) {
swap(&arr[0], &arr[i]);
// Heapify root element to get highest element at root again
heapify(arr, i, 0);
}
堆排序复杂度
O(nlogn) 对于所有情况(最佳情况,平均情况和最坏情况),堆排序都有时间复杂性。
包含 n 个元素的完全二叉树的高度为 logn,要完全堆放其子树已经是 max-heaps 的元素,我们需要继续比较该元素及其左右叶子节点,并将其向下推,直到其两个子元素均小于其大小。
在最坏的情况下,我们需要将元素从根移动到叶节点,进行多次 log(n) 比较和交换。
在 build_max_heap 阶段,我们对 n/2 元素执行此操作,因此 build_heap 步骤的最坏情况复杂度为n/2*log n ~ nlog n。
在排序步骤中,我们将根元素与最后一个元素交换并构建根元素。对于构建每个根元素,从叶子节点到根节点执行时间为 logn。因为我们重复 n 次,heap_sort 步骤也为nlogn。
同样,由于 build_max_heap 和 heap_sort 步骤是一个接一个地执行的,因此算法的复杂度不会增加,而是保持在 nlogn。
它还在 O(1) 空间复杂度上执行排序。与快速排序相比,它具有更好的最坏情况(O(nlogn))。快速排序 O(n^2) 在最坏的情况下具有复杂性。但是在其他情况下,快速排序速度很快。Introsort 是堆排序的替代方案,它结合了快速排序和堆排序以保留两者的优点:最坏情况下的堆排序速度和平均速度。
总结
简单总结大顶堆堆排序的基本思路:
a.将无需序列构建成一个大顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
参考:
[1] Jon Bentley, 黄倩, 钱丽叶. 编程珠玑 -- 2版(修订版)[M]. 北京: 人民邮电出版社, 2018(07):161-165,
[2] The Analysis of Heapsort


