TensorFlow学习笔记8-深度学习的正则化

深度学习的正则化

回顾一些基本概念

概念	描述
设计矩阵	数据集在特征向量上的表示
训练误差	学习到的模型与训练集标签之间的误差
泛化误差(测试误差)	学习到的模型与测试集之间的误差
欠拟合	模型的训练误差很大
过拟合	训练误差小，但训练误差与测试误差之间差距很大
容量	拟合各种函数的能力，容量越大，拟合函数的能力越大
交叉验证	当数据集不大时，将数据集分为k个，第i个作为测试集，其他作为训练集的方法
点估计	设模型中的真实参数\(\theta\)固定但未知，而点估计\(\hat{\theta}\)是数据的函数
偏差Bias	模型的(多次)测量(取平均)值与真实值之间的差：\(Bias(\hat{\theta})=E(\hat{\theta})-\theta\)
样本方差	\(\sigma_m^2=\frac{1}{m}\sum^m_{i=1}(x_i-\bar{x})^2\)
方差的无偏估计	\(\sigma_m^2=\frac{1}{m-1}\sum^m_{i=1}(x_i-\bar{x})^2\)
估计量\(\hat{\theta}\)的方差	\(Var(\hat{\theta})=E[(\hat{\theta}-E(\hat{\theta}))^2]\)
均方误差MSE	\(MSE=E[(\hat{\theta_m}-\theta_{data})^2]=Bias(\hat{\theta_m})+Var(\hat{\theta_m})+noise\)
正则化	正则化是指修改学习算法，使其降低泛化误差而非训练误差。如在线性回归中加入权重衰减取修改其训练标准，表示偏好于平方\(L^2\)范数较小的权重：\(J(w)=MSE_train+\lambda w^Tw\)

正则化是防止过拟合的。

正则化中新增概念	描述
数据集增强	创建假数据以实现更好的泛化：对数据进行变换或加噪声(如对图形进行旋转平移，加高斯噪声等)后作为训练数据集，保证分类效果不变
半监督学习	无标签的数据和有标签的数据都用于估计 \(p(y)\) 。学习的目的是使相同类中的样本有近似的表示
多任务学习	通过合并几个任务中的样例提高泛化。模型中的一部分用于其他任务时(叫做共享参数)，会有很好的约束进而提高泛化能力
提前终止	训练的数据强大而真实模型过于简单时，更多的数据反而会使泛化误差上升。因此在训练过程中找到测试误差最低对应的参数就可以提前终止训练。
参数绑定	训练两个相似的模型时，其\(w_A\)和\(w_B\)会接近，可以使用这种惩罚：\(\Omega(w_A,w_B)=|w_A-w_B|^2_2\)
稀疏表示	通过使用\(L^1\)范数，KL散度惩罚，正交匹配追踪等将\(w\)矩阵变得稀疏
Bagging	从原始数据集重复采样构成k个与原始数据集相同Size的数据集(有些原始数据集中的样例重复出现)，分别训练出k个模型，用k个模型的参数进行平均即可。任何机器学习算法都可以从模型平均中大幅获益。
Dropout	将原始模型中任意删除任意个非输出单元获得多种子网络模型。所有模型共享参数。每个子网络的训练好的参数可直接用于训练父网络。它是对Bagging的更高效的近似。
对抗训练	对人为制造出与原始样本近似的对抗样本(人觉得二者是同一类)进行预测发现有较大误差。用这种对抗样本进行训练的办法就是对抗训练。

重要的两个图：

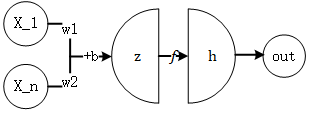
图1 神经元模型

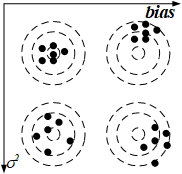
图2 方差与偏差的理解

有效的正则化能显著减小方差而不过度增大偏差。
下面介绍常用的正则化策略。

参数范数惩罚

该正则化方法在代价函数\(J\)增加一个参数范数惩罚\(\Omega(\theta)\)，

\[J(\theta,X,y) \leftarrow J(\theta,X,y)+\alpha \Omega(\theta) \]

其中\(\alpha \in [0,\infty)\)是权衡范数惩罚项和标准目标函数\(J(X,\theta,y)\)相对贡献的超参数。\(\alpha\)越大，惩罚越大。

参数包括仿射变换(\(z=XW+b\))中的权重与偏置，通常只惩罚权重。对权重的惩罚常有两种：

• \(L^2\)参数正则化(最常用的正则项)
  正则项为\(\Omega(\theta)=\frac{1}{2} ||w||^2_2\)，这种正则项的方法叫做岭回归。
  所以

  \[J'(\theta,X,y) \leftarrow J(\theta,X,y)+ \frac{\alpha}{2} w^Tw \tag{1} \]

  相应地，对式\((1)\)求梯度，得到

  \[\nabla_w J'=\alpha w+\nabla_wJ \]

  所以，更新权重的公式为：

  \[w'=w-\epsilon(\alpha w+\nabla_wJ)=(1-\epsilon \alpha)w-\epsilon \nabla_wJ \tag{2} \]

  直观上的理解是：\(L^2\)正则化目的在于减小了\(w^Tw\)的值，它将\(w\)的值较未正则化时将\(\boldsymbol{w}\)中较大的分量\(w_i\)进行收缩。

• \(L^1\)正则化
  正则项为\(\Omega(\theta)=||w||_1=\sum_i |w_i|\)
  此时，代价函数更新为：

  \[J'(\theta,X,y) \leftarrow J(\theta,X,y)+ \alpha||w||_1 \tag{3} \]

  对式\((3)\)求梯度，得到

  \[\nabla_w J'=\alpha \cdot sign(w)+\nabla_wJ \]

  更新权重的公式为:

  \[w'=w-\epsilon(\alpha \cdot sign(w)+\nabla_wJ) \tag{4} \]

  与\(L^2\)正则化相比，\(L^1\)正则化在\(\alpha\)足够大时会将特征\(w_i(w_i\ subject\ to\ w_i \leq \frac{\alpha}{H_{i,i}})\)推至0，它将\(\boldsymbol{w}\)中较小的分量\(w_i\)直接推至0。
  能产生更稀疏的\(\boldsymbol{w}\)(意即其中的分量有很多0)，可以用来进行特征选择，它将一部分没那么重要的特征的权重降为0。

作为约束的范数惩罚

回顾KKT，其中广义的Langrange函数为

\[L(\theta,\alpha;X,y)=J(\theta;X,y)+\alpha(\Omega(\theta)-k) \]

该约束问题的解为

\[\theta^*=\arg_{\theta} \min \max_{\alpha\geq 0}L(\theta,\alpha) \]

当\(\alpha=\alpha^*\)取到最优解时，最优解\(\alpha\)鼓励\(\Omega(\theta)\)收缩变小。这时：

\[\theta^*=\arg_{\theta}\min J(\theta;X,y)+\alpha* \Omega(\theta) \]

这就是之前的范数惩罚。若\(\Omega\)是\(L^2\)范数，则权重被约束在一个球中。若\(\Omega\)是\(L^1\)范数，则权重被约束在一个方框区域中。较大的\(\alpha\)将获得较小的约束区域。