TensorFlow学习笔记7-深度前馈网络(多层感知机)

深度前馈网络(前馈神经网络,多层感知机)

神经网络基本概念

前馈神经网络在模型输出和模型本身之间没有反馈连接;前馈神经网络包含反馈连接时，称为循环神经网络。

前馈神经网络用有向无环图表示。

设三个函数组成的链：\(f_3(f_2(f_1))\)，\(f_1\)为网络第一层，叫输入层。\(f_2\)为第二层，依次类推，中间层叫做隐藏层。最后一层为输出层。链的全长称为模型的深度。
每个隐藏层都有张量值，这些隐藏层的维数为模型的宽度。

概念	解释
输入层	网络的第一层
隐藏层	网络的中间N层
输出层	网络的最后一层
网络深度	网络的层数
网络宽度	隐藏层中张量的维数
激活函数	将线性分量处理为非线性的函数：sigmoid函数、ReLU函数、softmax函数
反向传播	将模型的输出作为模型的输入去更新权重的值，进而形成反馈
batch_size	每次训练在训练集中取batchsize个样本训练；
迭代次数	1个iteration等于使用batchsize个样本训练一次
epoch	1个epoch等于使用训练集中的全部样本训练一次

前馈神经网络实例：学习XOR

问题描述

• 训练集的设计矩阵

\(x_1\)	\(x_2\)	\(y\)
0	0	0
0	1	1
1	0	1
1	1	0

• 模型：\(y'=f(\boldsymbol{x;\theta})\)
• 代价函数(MSE)：\(J(\boldsymbol{\theta})=\frac{1}{4}\sum_{x \in X}(y-y')^2\)

选择模型

选择线性模型：$$f(x;w,b)=\boldsymbol{w^Tx}+b \tag{1}$$

其中\(\boldsymbol{x,w}\)为向量，\(b\)为标量。

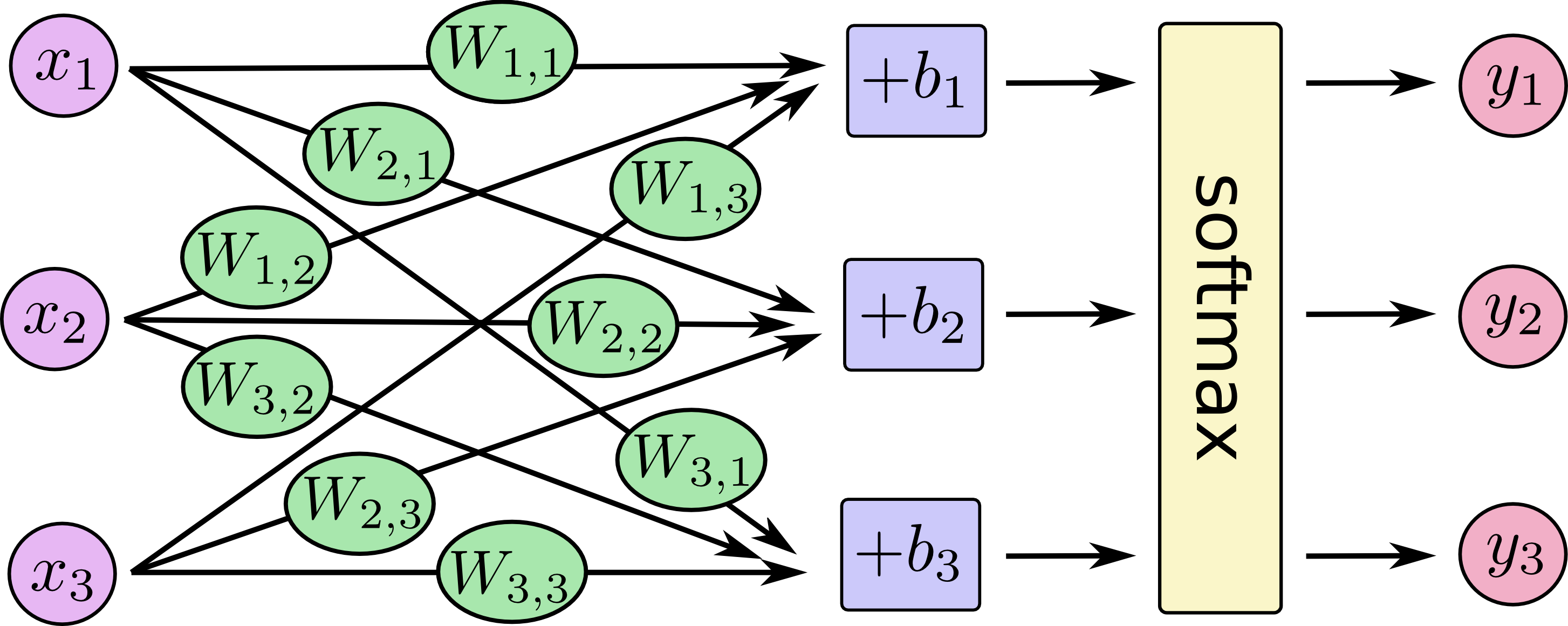
按TensorFlow的描述方法(具体)：

graph BT A((x)) --> C(MatMul) B((w)) --> C C --> E(Add) D((b)) --> E E --> F((y'))

在神经网络中只有1层(这是一个神经元)：

graph BT A((x)) --> D((y')) B((w)) --> D((y')) C((b)) --> D((y'))

更简单一些的描述为(标记这种图时，通常省略截距项)，一个函数操作意味着一层(更概念化一些)：

graph BT A((x)) --w--> B((y'))

通常用这幅图来描述一层神经网络。X节点是Y节点的父节点。
测试发现不能实现XOR函数。

选择前馈神经网络

即：

\[\boldsymbol{h}=f_1(\boldsymbol{x;W,c})=\boldsymbol{W^Tx+c} \]

\[y'=f_2(\boldsymbol{h;w},b)=\boldsymbol{w^Th}+b \]

graph BT A((x)) --W--> B((h)) B --w--> C((y'))

但是：\(f_1\)函数不能是线性的，因为作为输出层的\(f_2\)已经是线性的了(否则总体仍是线性模型)。
基于此，对\(f_1\)进行修改，\(h\)的值变为：

\[\boldsymbol{h}=f_3(\boldsymbol{W^Tx+c})=\max (0,\boldsymbol{W^Tx+c}) \]

\[y'=\boldsymbol{w^Th}+b \]

其中\(f_3(\boldsymbol{h})=\max (0,\boldsymbol{h})\)为激活函数；这个激活函数叫做整流线性单元(又叫ReLU)。现在，模型为：

\[y'=\boldsymbol{w}^T(\max (0,\boldsymbol{W^Tx+c}))+b \tag{2} \]

矩阵形式为：

\[\boldsymbol{y'}=\boldsymbol{W_2^T}\max (0,\boldsymbol{W_1^T X+c})+\boldsymbol{b} \tag{3} \]

graph BT A((X)) --W--> B((h)) B --w--> C((y'))

其中每一层都类似于这种结构：

一般地，一个神经元的结构如下图所示。

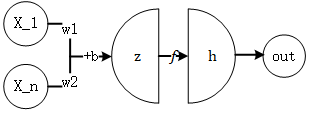
• \(\boldsymbol{x}\) 是训练数据集的样例；
• \(\boldsymbol{w}\) 和 \(b\) 是参数，常放在一起组成参数的集合\(\theta\)；
• \(\boldsymbol{z}=\boldsymbol{w^Tx}+b\) 是线性函数输出量；
• \(h=f(z)\) ，其中\(f\)是激活函数；
• \(out=h\) 是输出量；

这样的每一个单元叫做一个神经元。每一层中单元的个数为神经网络的宽度。

\(h\)的维度就是该层神经网络中的神经元个数，也是该层的宽度。

\(h\)的维度就是该层神经网络中的神经元个数，也是该层的宽度。

\(h\)的维度就是该层神经网络中的神经元个数，也是该层的宽度。

训练模型

代价函数

训练模型的本质是根据训练集和标签的分布设计合适的概率分布模型，并不断优化该模型。

用于非凸函数的随机梯度下降没有收敛性的保证，且对参数的初始值很敏感。

重要： 将所有权重初始化为小随机数，将偏置(截距)初始化为0或小的正值。

重要： 在深度学习中，都是条件分布(已知x,求y的概率分布)，所以最大似然估计(最小化负的对数似然)完全等价于交叉熵。

使用最大似然学习条件分布
代价函数：负的对数似然，与交叉熵等价
$$J(\theta)=-E_{x,y\sim \hat{p}{data}}\log p(y|x)=-\sum_i p_{data}(y|x)\log p_{model}(y|x)$$

• \(p_{model}(y|x)\)的意义为：给定\(x\)时，按模型预测得到的\(y\)关于类别class的概率分布。在笔记3中就是矩阵Z的每一行预测的概率分布；
• \(p_{data}(y|x)\)的意义为：给定\(x\)时，数据集中的\(y\)关于类别class的概率分布。在笔记3中就是标签给出的以独热码表示的概率分布。

当\(p_{model}(y|x)\)给出正态分布(意即\(p(y|x)=N(y;f(x;\theta,\sigma^2)\)服从正态分布)时，\(J(\theta)\)变化为最小化均方误差：

$$J(\theta)=\frac{1}{2}E_{x,y\sim \hat{p}_{data}}||y-y'||^2+const$$

优点：斜率较小(梯度较小)的函数的梯度变得很小，导致隐藏单元或输出单元的激活函数会饱和(导致学习速度过慢或学习停滞)，
而交叉熵可以避免这个问题。
例如：很多输出单元包含指数函数，在很小的负值时会造成饱和，这时本代价函数中的对数会消掉指数效果。

缺点：通常没有最小值。例如：模型中学习正态分布中方差参数时，可能对正确的训练集输出赋予极高的概率密度，
这将导致交叉熵为负无穷，会不断进行优化，导致没有最小值。后面会讲怎么处理这个问题。

输出层

设隐藏层给出隐藏特征\(\boldsymbol{h}=f(\boldsymbol{x};\theta)\)，则输出层负责将前一层的隐藏特征输出为预测结果。

• 用于输出高斯分布的线性输出单元(输出变量为高斯分布中的均值)

  输出层为一个向量$$\boldsymbol{y'=W^Th+b} \tag{4}$$经常用来产生条件高斯分布的均值\(p(y|x)=N(y;y',I)\)

  相应地，最大化负的对数似然(损失函数)等效于最小化均方误差:

  \[J(\theta)=\frac{1}{2}E_{x,y\sim \hat{p}_{data}}||y-y'||^2+const \tag{5} \]

• 用于输出伯努利分布的sigmoid输出单元(输出变量\(y'\)服从二值分布，二分类问题)

  只需预测一个值\(P(y=1|\boldsymbol{x})\)，\(P(y=0|\boldsymbol{x})=1-P(y=1|\boldsymbol{x}))\)，这时的输出层为一个标量

\[y'=sigmoid(\boldsymbol{w^Th}+b) \tag{6} \]

记 \(z= \boldsymbol{w^Th}+b\) 。但这是未归一化的。现为了归一化，设非归一化的对数概率对\(y,z\)是线性的，则归一化的概率分布为

\[\begin{aligned} P(y|x)&=\frac{\exp(yz)}{\sum^1_{y'=0} \exp(y'z)} \\ &=\frac{\exp(yz)}{\exp(yz)+\exp((1-y)z)} \\ &=sigmoid ((2y-1)z) \end{aligned} \]

即\(P(y=1|x)=sigmoid(z)=y'\)，sigmoid输出层输出的就是伯努利分布的\(P(y=1|x)\)。

对二值型的标签y，y=1的经验概率分布要么(0,1)，要么为(1,0)，则交叉熵为：

\[H=-\sum^1_{i=0} P_{data,y=i}\log P(y=i|x)=-\log P(y|x) \]

相应地，负的对数似然(损失函数)为

\[J(\theta)=-\log P(y|x)=-\log (sigmoid ((2y-1)z))=\zeta ((1-2y)z) \tag{7} \]

只要输出单元是sigmoid单元，就使用最大似然优化。

• 用于输出多项式分布的softmax输出单元(输出变量\(y'\)有n个取值，多分类问题)

  前一层给定隐藏特征 \(\boldsymbol{h}\) ，线性层预测未归一化的对数概率：

  \[\boldsymbol{z=W^Th+b}, here\ z_{i}=\log P(y=i|x) \]

  然后利用softmax函数进行指数化、归一化：

  \[softmax(\boldsymbol{z})_i = \frac{\exp (z_i)}{\sum_j \exp (z_j)} \tag{8} \]

  相应地，负的对数似然(损失函数)为

  \[J(\theta)=-\log (softmax(\boldsymbol{z})_i)=\log \sum_j \exp (z_j)-z_i \tag{9} \]

• 用于输出多峰回归的高斯混合输出单元

  具有n个分量的高斯混合输出由下面的条件分布定义：

  \[p(\boldsymbol{y}|\boldsymbol{x})=\sum_ {i=1}^n p(c=i|\boldsymbol{x})N(\boldsymbol{y};\boldsymbol{\mu_i(x),\sum_i(x)}) \]

  神经网络必须有3个输出：

  • 混合组件\(p(c=i|\boldsymbol{x})\)：这个分布通常由n维向量的softmax获得。
  • 均值\(\mu\)：指明了第i个高斯组件的中心值，若y是d维的向量，则网络应输出一个n*d的\(\mu\)矩阵。
  • 协方差\(\sum_i (x)\)：每个组件i的协方差矩阵。通常使用对角矩阵来避免计算行列式。

隐藏层

用于输出层的单元模型都可用于隐藏层。但具体用哪种呢？要凭直觉猜！！

完全凭直觉吗？一般地，整流线性单元ReLU通常是很好的默认的选择。

但是要注意以下性质： 整流线性单元ReLU在x=0处不可微分；但其实局部不可微的性质并不会影响全局的工作。

• ReLU整流线性单元

  整流线性单元通常作用在仿射变换 \(\boldsymbol{W^Tx+b}\) 上，即 \(\max(0,\boldsymbol{W^Tx+b})\) 。

  初始化时，可以将\(b\)初始化为很小的正值，这样在初始时就能保证激活状态。

  以下是几个扩展的整流单元。

  名称	表达式	描述
  绝对值整流	\(f(x)=\max(0,x)-\min(0,x)\)	用于图像中的对象识别，寻找照明极性翻转下不变的特征，如物体的轮廓
  渗漏整流线性单元	\(f(x)=\max(0,x)+a*\min(0,x)\),\(a\)为小值(如0.01)	无
  参数化整流线性单元	\(f(x)=\max(0,x)+a*\min(0,x)\),\(a\)为学习的参数	无
  maxout单元(分段线性激活函数)	\(g(\boldsymbol{z})_i=\max_{j \in G_i}z_j\)	将\(\boldsymbol{z}\)分为每组有k个值得组，输出每个组中的最大元素

• sigmoid与双曲正切函数

  sigmoid函数和双曲正切函数分别为\(g(z)=sigmoid(z)\)，\(g(z)=\tanh(z)\),二者关系是\(\tanh(z)=2*sigmoid(2z)-1\)。

  sigmoid在z的绝对值很大时，会饱和到0或1,只有z接近0，sigmoid函数才会较为敏感。这种广泛的饱和性会使基于梯度的学习非常困难。不鼓励它作为隐藏单元。

  必须使用sigmoid函数时，可以选择使用双曲正切函数，它表现更好。有时分段线性激活函数不能使用时，或许可选sigmoid函数(例如：循环网络，自编码器等)。

• 其他常见的隐藏单元的激活函数(该领域研究很多的一个方向)

  • 径向基函数：\(h_i=\exp (-\frac{1}{\sigma^2_i}||W_{:,i}-x||^2)\)，在x接近W时较活跃；但对大部分x都饱和到0,所以很难优化。
  • softplus函数：\(g(a)=\zeta (a)=\log (1+e^a)\)。它表明隐藏单元类型的性能可能是非常反直觉的。
  • 硬双曲正切函数：\(g(a)=\max (-1,\min (1,a))\)。

架构设计

• 万能近似定理表明：无论我们试图学习什么函数，一定有一个大的MLP(多层感知机)可以表示该函数。
• Montufar的定理指出：具有\(d\)个输入，深度为\(l\)，每个隐藏层具有\(n\)个神经元的深度整流网络可描述的线性区域的数量为

\[\left( \begin{matrix} \left( \begin{matrix} n \\ d \end{matrix} \right)^{d(l-1)} n^d \end{matrix} \right) \]

即它是深度\(l\)的指数级。

反向传播

反向传播允许代价函数的信息通过网络向后流动，以便计算梯度。

反向传播仅指用于计算梯度的方法。

根据链式法则，如果 $ \boldsymbol{y} =g( \boldsymbol{x} ) $ , \(z=f( \boldsymbol{y} )\) ，则

\[\frac{\partial z}{\partial x_i}=\sum_j \frac{\partial z}{\partial y_j} \frac{\partial y_j}{\partial x_i} \]

向量写法为：

\[\nabla_\boldsymbol{x}z=(\frac{\partial y}{\partial x})^T\nabla_y z \]

同样地，扩展其维度：

\[\nabla_\boldsymbol{X}z=\sum_i (\nabla_XY_j)\frac{\partial z}{\partial Y_j} \]

接下来用伪代码描述计算反向传播的算法：

• 首先定义一个计算图，该图中共有\(n\)个单元，每个单元的函数为\(f_i\)，输入层的单元共有\(k\)个。输入向量 \(\boldsymbol{x}\) 输入前\(k\)个单元。

  $for\ i=1,...,n_i\ do $

  \(\quad u_i \leftarrow x_i\)

  \(end\ for\)

  \(for\ i=n_i+1,...,n\ do\)

  \(\quad A_i \leftarrow \{u_j|j \in Pa(u_j)\}\)

  \(\quad u_i \leftarrow f_i(A_i)\)

  \(end\ for\)

  \(return\ u_n\)

• 下面是反向传播的简化版本：

  运行上方代码激活网络；

  初始化grad_table，用于存储计算好的导数的数据结构。grad_table[\(u_i\)]存储 \(\frac{u_n}{u_i}\) 的结果；

  grad_table[\(u_n\)] $\leftarrow$1；

  \(for\ j=n-1\ down\ to\ 1\ do\)

  \(\quad\)计算\(\frac{\partial u_n}{\partial u_j}=\sum_{i:j\in Pa(u_i)}\frac{\partial u_n}{\partial u_i}\frac{\partial u_i}{\partial u_j}\)：

  \(\quad\)grad_table[\(u_j\)]\(\leftarrow \sum_{i:j\in Pa(u_i)}\)grad_table\([u_i]\frac{\partial u_i}{\partial u_j}\) #j是i的父节点，对i求和

  \(end\ for\)

  \(return\) {grad_table[\(u_i]|i=1,...,n_i\)}

  反向传播算法减少了公共子表达式，大约对计算图中每一个节点执行一个Jacobian乘积。避免了重复子表达式的指数爆炸。
  

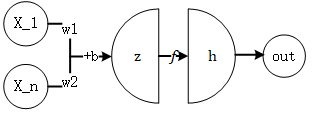
  每个神经元的反向传播算法为：

  \[\frac{\partial out}{\partial w_i}=\frac{\partial h}{\partial z}\frac{\partial z}{\partial w_i}=f'(z)\frac{\partial z}{\partial w_i} \]

• 反向传播算法的进一步细化版本：

  \(g \leftarrow \nabla_{y'}L(y',y)\) #计算顶层的梯度

  \(for\ k=l,l-1,...,1\ do\) #共\(l\)层

  \(\quad g\leftarrow \nabla_{z_k} J=g\cdot f'(z_k)\) #乘以每一层的激活函数的导数

  \(\quad \nabla_{b_k} J=g+\lambda \nabla_{b_k} \Omega(\theta)\) #加上了正则项

  \(\quad \nabla_{W_k} J=g+\lambda \nabla_{W_k} \Omega(\theta)\) #加上了正则项

  \(\quad g\leftarrow \nabla_{h_{k-1}} J=W_k^Tg\) #下一个更低层的隐藏层的传播梯度

  \(end\ for\)

  案例：TensorFlow实现多层感知机(源自<TensorFlow实战> 黄文坚)

# MLP mnist
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

# 1 Collect data
mnist = input_data.read_data_sets("MNIST_data/",one_hot=True);

# 2 Create Model
X = tf.placeholder(tf.float32,[None,784]);
y = tf.placeholder(tf.float32,[None,10]);
keep_prob = tf.placeholder(tf.float32);

# Layer 1: The hidden layer includes 300 nodes, 隐藏层包括300个节点, 矩阵W的列数
#  第一层隐藏层使用ReLU作为激活函数, 并使用Dropout技术(笔记8中内容)随机丢弃部分节点
W1 = tf.Variable(tf.truncated_normal([784,300],stddev=0.1));
b1 = tf.Variable(tf.zeros([300]));
z1 = tf.matmul(X,W1)+b1;
h1 = tf.nn.relu(z1);
h1_drop = tf.nn.dropout(h1,keep_prob);

# Output Layer
W2 = tf.Variable(tf.zeros([300,10]));
b2 = tf.Variable(tf.zeros([10]));
z2 = tf.matmul(h1_drop,W2)+b2;
y_ = tf.nn.softmax(z2);

# 3 Loss function
loss = -tf.reduce_mean(tf.reduce_sum(y*tf.log(y_),1));
optimizer = tf.train.GradientDescentOptimizer(0.3);
train = optimizer.minimize(loss);

# 4 Initial
init = tf.initialize_all_variables();
sess = tf.InteractiveSession();
sess.run(init);

# 5 Train
total_step = 3000;
for step in range(total_step):
    x_batch,y_batch = mnist.train.next_batch(100);
    sess.run(train,feed_dict={X:x_batch,y:y_batch,keep_prob:0.75});
    if step % (total_step/100) == 0 :
        print("Process-", step/(total_step/100),"%  loss=",sess.run(loss,feed_dict={X:x_batch,y:y_batch,keep_prob:0.75}));

# 6 Accuracy
correct_predition = tf.equal(tf.argmax(y,1),tf.argmax(y_,1));
accuracy = tf.reduce_mean(tf.cast(correct_predition,tf.float32));
print("Accuracy:",accuracy.eval({X:mnist.test.images,y:mnist.test.labels,keep_prob:1}));

可以看到打印的正确率已经提升到了97.6%左右。