TensorFlow学习笔记5-概率与信息论

TensorFlow学习笔记5-概率与信息论

本笔记内容为“概率与信息论的基础知识”。内容主要参考《Deep Learning》中文版。

  • \(X\)表示训练集的设计矩阵，其大小为m行n列，m表示训练集的大小(size)，n表示特征的个数；
  • \(W\)表示权重矩阵，其大小是n行k列，n为输入特征的个数，k为输出(特征)的个数；
  • \(\boldsymbol{y}\)表示训练集对应标签，其大小为m行，m表示训练集的大小(size)；
  • \(\boldsymbol{y’}\)表示将测试向量\(x\)输入后得到的测试结果；
  • 频率派概率：概率直接与事件发生的频率相联系。贝叶斯概率：概率与事件发生的确定性水平相联系。

概率分布：随机变量(或一簇随机变量)在每个取值的可能性大小。

  • 离散型变量：\(P(x=x_1)\)，\(x\sim P(x)\)表示随机变量\(x\)服从的概率分布。

    • 归一化：\(\sum_ {x_ {i} \in X} P(x_ {i})=1\)
    • 多个随机变量的概率分布称为联合概率分布。即\(P(x,y)\)

  • 连续型变量：概率密度函数(Probability density function, PDF) \(p(x)\)表示无穷小区域的概率为 \(p(x)\delta x\)。

  • 边缘概率：

    • 离散型：\(P(x)=\sum_y P(x,y)\)
    • 连续型：\(p(x)=\int p(x,y)dy\)

  • 条件概率：
    \(P(y=y_ 0|x=x_ 0)=\frac{P(y=y_ 0,x=x_ 0)}{P(x=x_ 0)}\)

  • 条件概率的链式法则：
    \(P(a,b,c)=P(a|b,c)P(b,c)P(c)\)

    \[p(\boldsymbol{x})=p(x_ {1})\prod^{n}_ {i=2}p(x_ {i}|x_ {1},...,x_ {i-1}) \]

  • 贝叶斯规则:

    \[P(x|y)=\frac{P(x)P(y|x)}{P(y)} \]

  • 变量的独立性：

    • \(p(x,y)=p(x)p(y)\)，记为\(x \bot y\)
    • 条件独立性：\(p(x,y|z)=p(x|z)p(y|z)\)，记为\(x \bot y |z\)

  • 期望：

    • 离散型：\(E_{x \sim P}[f(x)]= \sum_x P(x)f(x)\)
    • 连续型：\(E_ {x \sim p}[f(x)]=\int p(x)f(x)dx\)
    • 线性的：\(E[af(x)+bg(x)]=aE[f(x)]+bE[g(x)]\)

  • 方差：\(Var(f(x))=E[(f(x)-E(f(x)))^2]\)

  • 协方差：\(Cov(f(x),g(y))=E[(f(x)-E(f(x)))(g(y)-E(g(y)))]\)

    相互独立的两个随机变量协方差一定为0。协方差为0的两个变量不一定独立。

  • 协方差矩阵\(Cov(x)_ {i,j} = Cov(x_ i, x_ j)\)，其对角元是方差\(Cov(x_ i, x_ i)=Var(x_i)\)

几种分布

  • 伯努利分布(二值分布)：

\[P(x=1)=\phi \]

\[P(x=0)= 1-\phi \]

  • 高斯分布(正态分布)：

\[f(x)=\sqrt{\frac{1}{2 \pi \sigma ^2}} \exp({- \frac{(x-\mu)^2}{2\sigma ^2}}) \]

其中$\mu$为期望，$\sigma ^2$为方差，$\beta = 1/\sigma^2$为精度。
标准正态分布为$\mu=0,\sigma =1$的正态分布。
  • 多维正态分布：

\[\boldsymbol{N(x;\mu,\Sigma)=\sqrt{\frac{1}{2 \pi \det(\Sigma)}} \exp({- \frac{(x-\mu)^T \Sigma^{-1} (x-\mu)}{2}})} \]

其中$\boldsymbol{\mu}$为期望，向量形式，$\boldsymbol{\Sigma}$是分布的协方差矩阵。
  • 指数分布：

\[p(x;\lambda)=\lambda \exp(-\lambda x), subject\ to\ x \geq 0 \]

  • LapLace分布：

\[Laplace(x;\mu,\gamma)=\frac{1}{2\gamma} \exp(- \frac{|x-\mu|}{\gamma}) \]

  • Dirac分布：

\[p(x)=\delta (x-\mu) \]

  • 经验分布：

\[\hat{p}(x)=\frac{1}{m}\sum^m_ {i=1} \delta (x-x^{(i)}) \]

  • 混合分布：

\[P(x)=\sum_ {i} P(c=i)P(x|c=i) \]

混合分布由一系列形如$P(x|c=i)$的组件分布组成。常见的高斯混合模型的组件$P(x|c=i)$是高斯分布。**可用来拟合多峰函数。**
高斯混合模型是概率密度的通用近似器。

常用的函数

  • logistic sigmoid函数：\(\sigma(x)=\frac{1}{1+\exp (-x)}\)

  • softplus函数：\(\zeta(x) = \log (1+ \exp (x))\)可用来产生正态分布的\(\beta\)和\(\sigma\)参数。

    • $ \sigma (x)=\frac{ \exp (x)}{\exp(x)+\exp(0)}$
    • $ \frac{d}{dx}\sigma (x)=\sigma (x)(1-\sigma (x))$
    • $ 1-\sigma (x)=\sigma (-x)$
    • $ \log \sigma (x)= -\zeta(-x)$
    • $ \frac{d}{dx}\zeta(x)=\sigma(x)$
    • $ \forall x \in (0,1),\sigma^{-1}(x)= \log (\frac{x}{1-x})$
    • $ \forall x>0, \zeta^{-1}(x)=\log (\exp (x)-1)$
    • $ \zeta(x)=\int^x_ {-\infty} \sigma(y)dy$
    • $ \zeta (x)-\zeta (-x)=x$

确定函数关系的两个随机变量的概率分布函数

  • 设\(y=g(x)\)，要保证\(|p_ y (g(x))dy| = |p_ x(x)dx|\) ，可以得到

\[p_y(y) = p_ {x}(g^{-1}(y))|\frac{\partial{x}}{\partial y}| \]

或

\[p_x(x) = p_ {y}(g(x))|\frac{\partial{g(x)}}{\partial x}| \]

高维空间中，扩展为：

\[p_x(\boldsymbol{x}) = p_ {y}(g(\boldsymbol{x}))|\det(\frac{\partial{g(\boldsymbol{x})}}{\partial \boldsymbol{x}})| \]

信息论基础

  1. 事件\(x=x_0\)的自信息为\(I(x)=-\log P(x)\)。当底数为\(e\)时，信息量单位为奈特(nats)，底数为2时，单位为比特或香农。这里底数为\(e\)。

  2. 香农熵为$$H(x)=E_ {x \sim P}[I(x)]=-\sum_ {i} P(x_ {i})\log P(x_ {i})$$

  3. 对同一个随机变量的两种单独的概率分布\(P(x)\)和\(Q(x)\)，其差异用KL散度衡量：$$D_ {KL}(P||Q)=E_ {x \sim P}[\log \frac{P(x)}{Q(x)}]
    =E_ {x \sim P}[\log P(x) - \log Q(x)]=\sum_ {i} P(x_ {i})(\log P(x_ {i})- \log Q(x_ {i}))$$
    注意计算\(D_ {KL}(P||Q)\)还是\(D_ {KL}(Q||P)\)是不一样的，因为\(D_ {KL}(P||Q) \neq D_ {KL}(Q||P)\)
    。KL散度是不对称的。
    一般已经拿到了\(p(x)\)的分布，用\(q(x)\)去近似。可以选择最小化\(D_ {KL}(P||Q)\)或\(D_ {KL}(Q||P)\)。

    在机器学习中，\(P(x),Q(x)\)分别为基于数据集的经验分布(已知的)与设计的模型概率分布(估计的)。
    最大化似然就是最小化KL散度，由于\(\sum_i P(x_i)logP(x_i)\)与模型无关，故最小化KL散度就是最小化交叉熵。

  4. 交叉熵：

\[H(P,Q)=-E_ {x \sim P}[\log Q(x)]=-\sum_ {i} P(x_ {i})\log Q(x_ {i}) \tag{1} \]

综上：在机器学习中，最大似然估计，等价于最小化交叉熵。即：任何时候优化函数就是交叉熵，也就是对数似然组成的损失函数(即式\((1)\))。

结构化概率模型-分解联合概率分布的计算

若3个随机变量a,b,c满足：a影响b的取值，b影响c的取值，但a和c在给定b时是条件独立的(\(p(a,c|b)=p(a|b)p(c|b)\))，则：

\[p(a,b,c)=p(a)p(b|a)p(c|b) \]

  • 有向图模型分解：\(p(\boldsymbol{x})=\prod_ {i} p(x_i |Pa\ g(x_i))\)，其中\(Pa\ g(x_i)\)为节点$x_i $的父节点。
  • 无向图模型分解：图中 任何两两节点之间有边连接的节点的集合称为团，每个团有一个因子\(\phi^{(i)}(C^{(i)})\)，这些因子是非负的。
    整体的联合分布为\(p(\boldsymbol{x})=\frac{1}{Z}\prod_ {i}\phi^{(i)}(C^{(i)})\)，其中\(Z\)为归一化常数。

独立同分布与估计

通常我们有样本，却不知道其中的概率密度模型如何。设每次采样是独立同分布的。

测试集样本独立同分布很多时，中心极限定理：样本均值接近高斯分布。

统计中的量：

  1. 样本均值：m个样本的平均值\(\bar{x}=\frac{\sum_ {i}x_ {i}}{m}\)
  2. 样本方差：\(\sigma ^2 = \frac{1}{m}\sum^m_ {i=1}(x_ {i}-\bar{x})^2\)

概率论中的量：

  1. 数学期望：\(E(f(x))=\sum_ {i}f(x_ {i})P(x_ {i})\)或\(E(f(x))=\int f(x)p(x)dx\)
  2. 方差：\(var [f(x)]=E[(f(x)-E[f(x)])^2]\)

常用样本均值估计：

  • 二值分布的独立同分布的模型的 \(\theta\)参数 ；无偏估计。
  • 高斯分布的 \(\mu\)参数 。无偏估计。

常用样本方差估计：

  • 高斯分布的 \(\sigma ^2\)参数 ，有偏估计。
  • 用 \(\frac{m}{m-1}\times\)样本方差 去估计高斯分布的 \(\sigma ^2\)参数，无偏估计。
  • 虽然有偏，但还是用样本方差估计高斯分布的 \(\sigma ^2\)参数较多(样本量较大时，近似无偏)。
  1. 估计量的偏差：\(bias(\hat{\theta}_ {m})=E(\hat{\theta}_ {m})-\theta\)

其中,\(\hat{\theta}_ {m}\)为你从m个样本数据中计算出来的估计量，\(\theta\)为你要估计的模型中的参数。

  1. 估计量的方差用公式\(Var [\hat{\theta}_ {m}]=E[(\hat{\theta}_ {m}-E[\hat{\theta}_ {m}])^2]\)计算。
  2. 估计量的标准差为：\(\sigma = \sqrt{Var(\hat{\theta})}\)
  • 例如：样本均值的标准差为\(SE(\bar{x})=\sqrt{Var(\bar{x})}=\frac{\sigma}{\sqrt{m}}\)

那么优化时，选择优化估计量的偏差还是优化估计量的方差呢?

  • 如果选择最优化偏差，则方差可能很大，更关注整体，是一种欠拟合(训练误差较大)；
  • 如果选择最优化方差，则偏差可能很大，更关注细节，是一种过拟合(训练误差与测试误差差距较大)。
  • 选择最优化 均方误差(Mean Squared Error) 可以获得一种均衡。

\[MSE=E[(\hat{\theta}_ {m}-\theta)]=bias(\hat{\theta})_ {m}^2 + Var(\hat{\theta}_ {m}) \]

对均方误差的进一步解释

以回归任务为例：对测试样本\(x\)，令\(y_ {D}\)为\(x\)在数据集中的标记，\(y\)为\(x\)的真实模型中标记，\(f(x;D)\)为训练集\(D\)上的模型的预测输出。

方差

在一个训练集\(D\)上模型 \(f\) 对测试样本 \(x\)的预测输出为 \(y'=f(x;D)\), 那么学习算法 \(f\) 对测试样本 \(x\) 的 期望预测 为:

\[\bar{f}(x)=E_ {D}[f(x;D)] \]

上面的期望预测也就是针对 不同数据集 \(D\), \(f\) 对 \(x\) 的预测值取其均值, 也被叫做 均值预测.

使用样本数相同的不同训练集产生的方差为:

\[Var(x)=E_ {D}[(f(x;D)−\bar{f}(x))^2] \]

噪声

噪声为真实标记与数据集中的实际标记间的偏差:

\[ϵ^2=E_ {D}[(y_ {D}−y)^2] \]

为方便起见，设噪声期望为0，即\(E_ {D}[y_ {D}-y]=0\)

偏差

期望预测与真实标记的误差称为偏差(bias), 为了方便起见, 我们直接取偏差的平方:

\[bias^2(\bar{f}(x))=(\bar{f}(x)−y)^2 \]

估计的评价：均方误差(Mean Squared Error)

参考周志华老师书里的 期望泛化误差：均方误差[1]：

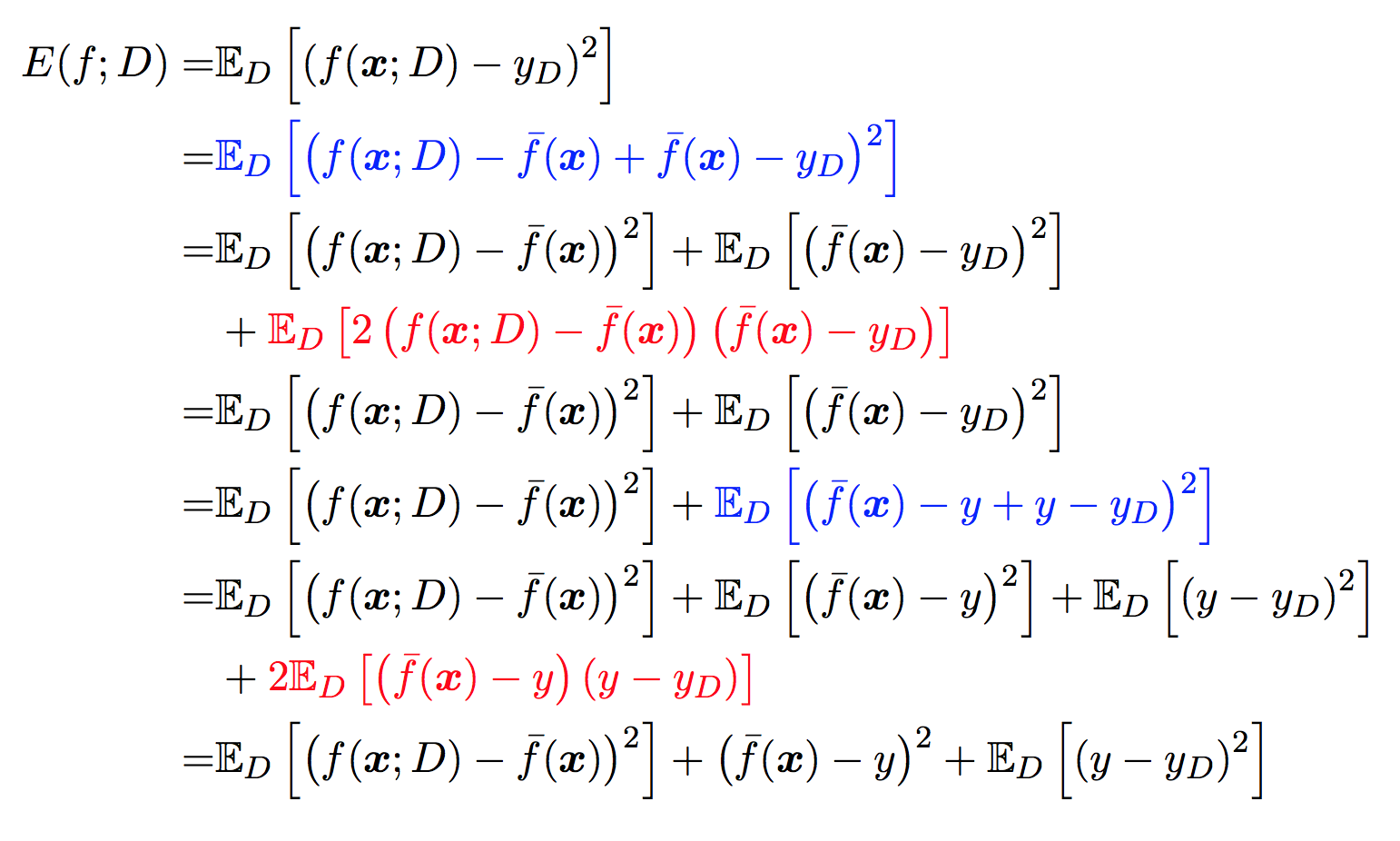
\[=Var(f(x;D))+bias^2(\bar{f}(\boldsymbol{x}))+\epsilon^2 \]

其中应用到了\(E_{D}[y_D -y]=0\)和\(E[f(x;D)]=\bar{f}(x)\)。

实际应用时 直接计算均方误差

\[MSE_ {train}=\frac{1}{m} \sum^m_{i=1}||y'_i-y_i||^2 \]

学习算法的平方预测误差期望为(记\(y'=f(x;D)\))[2]：

\[\begin{aligned} Err(x)&=E[(y−f(x;D))^2]=E[(y−y')^2] \\ &=E[y'^2]-2E[yy']+E[y^2] \\ &=E[y'^2]-E(y')^2+E(y')^2-2yE[y']+y^2 \\ &=E[(y'-E(y'))^2]+[E(y')-y]^2 \\ &=Var(y')+bias(y')^2 \end{aligned} \tag{1} \]

两者的差别在于：式\((1)\) 没有考虑\(y_D\) 与 \(y\) 之间的误差，这就是噪声。

  1. 源自《机器学习》周志华，第45页。个人更喜欢这个解释。 ↩︎

  2. 源自《深度学习》伊恩·古德费洛，第81页。 ↩︎

posted @ 2019-08-30 15:18  云远·笨小孩  阅读(784)  评论(0)  编辑  收藏  举报