TensorFlow学习笔记4-线性代数基础

TensorFlow学习笔记4-线性代数基础

---

本笔记内容为“AI深度学习”。内容主要参考《Deep Learning》中文版。

• \(X\)表示训练集的设计矩阵，其大小为m行n列，m表示训练集的大小(size)，n表示特征的个数；
• \(W\)表示权重矩阵，其大小是n行k列，n为输入特征的个数，k为输出(特征)的个数；
• \(\boldsymbol{y}\)表示训练集对应标签，其大小为m行，m表示训练集的大小(size)；
• \(\boldsymbol{y’}\)表示将测试向量\(x\)输入后得到的测试结果；

---

几个概念

1. 深度学习

如果想让计算机构建较简单的概念来学习复杂概念，我们可能需要一个深的(层次很多的)计算图，这种方法叫做AI深度学习。典型例子是前馈神经网络和多层感知机(multilayer perceptron, MLP)。

神经网络的深度的度量：

• 计算图的深度(计算层次)
• 概念图的深度(模型层次)

深度学习、机器学习与AI的关系如图：

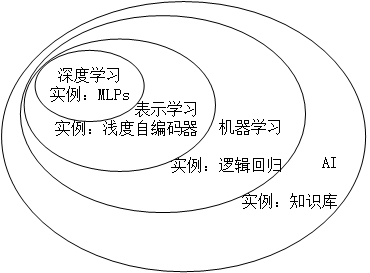
2. 表示学习

机器学习需要特征集，但我们很难知道应提取什么特征。如：我们想识别出图片中是否有汽车，想到用车轮是否存在作为一个特征，但如何根据像素值去描述什么是车轮呢？这就需要表示学习。表示学习可帮助发现很好的特征集。

3. 自编码器

表示学习的典例是自编码器(autoencoder)。它希望：

1. 输入数据\(X\)和输出数据\(X’\)尽可能保持一致；
2. 新的表现形式\(Y\)具有各种好的特性。
   

线性代数基础

• 标量： 一个数字，用斜体表示，如\(x,y,i,j,k,m,n\)等。
• 向量：一 列 数字。用粗体表示，如\(\boldsymbol{x,y,b}\)等。如果向量有n个元素且都属于\(\boldsymbol{R}\)，则该向量\(\boldsymbol{x \in{R^n} }\)。

表示方法：

• \(x_i\) is 第\(i\)个元素。
• \(x_{-1}\) is 除\(x_1\)之外的所有元素。
• 向量永远是一列的：\(x=(1,2,3)^T\)

• 矩阵：\(\boldsymbol{A}\)，\(\boldsymbol{A \in{R^{m \times n} } }\)

表示方法：

• \(A_{i,j}\)表示第i行第j列的元素。
• \(A_{i,:}\)表示第i行的向量。

• 矩阵的操作：

• 转置：\(A^T_{i,j}=A_{j,i}\)
• 广播：\(C=A+b\)，相当于 \(C_{i,j}=A_{i,j}+b_j\)
• 乘法：服从分配律、结合律，不服从交换律。
• 单位阵：\(I_n\)
• 逆矩阵：\(A^{-1}A=I_n\)

• 方程式 \(Ax=b\) 的解形式为：\(x=A^{-1}b\)，前提是矩阵A有逆矩阵。

解的个数有三种情况：
* 0个解(解不存在)；
* 1个解；
* 无穷个解；
* C个解(\(1<C<\infty\))：该情况：若x,y是其解，则\(z=\alpha x+(1-\alpha )y, \alpha 取任意实数\) 也是解

\(Ax=b\)有且仅有1个解的充要条件是矩阵A有逆。

• 线性组合：方程\(Ax=b\)可写作\(Ax=\sum_i x_i A_{:,i}=b\)

  • 生成子空间是一组向量线性组合后能抵达的点的集合。故

    \(\boldsymbol{Ax=b}\)是否有解 相当于 向量b是否在矩阵A的列向量的生成子空间中。

• A的值域(列空间)：矩阵A的列向量的生成子空间。

• 奇异：如果方阵的列向量线性相关，则称方阵是奇异的。否则是非奇异的。

---

要使\(Ax=b\)对任意的\(b \in R^m\)均有解，则要求A的列空间涵盖整个\(R^m\)空间，即矩阵A至少有m列线性无关的列向量。故\(n \geq m\)。

要使\(Ax=b\)对任意的\(b \in R^m\)均只有1个解，则要求A的列空间构成整个\(R^m\)空间，
即矩阵A恰好有m列线性无关的列向量。所以非奇异的 m*m的方阵对任意\(b \in R^m\)均只有1个解，此时A一定有逆矩阵。

---

• 范数：衡量向量的大小。\(L^p\)范数定义为

\[{ {\boldsymbol{||x||} }_ {p} }=(\sum_ {i}{|x_ {i}|^p})^{1/p} \]

其中\(p\in R, p \geq 1\)。

常用的是\(L^2\)范数，称为欧几里得范数。其平方常称为平方\(L^2\)范数，可通过\(x^T x\)计算。
当区分小值和0的时候，由于平方\(L^2\)范数在原点附近增长很慢，常用\(L^1\)范数：

\[||x||_ {1}=\sum_ {i} |x_ {i}| \]

最大范数表示向量中具有最大幅值的元素的绝对值：

\[||x||_ {\infty}=\max_ {i} |x_ {i}| \]

Frobenius范数衡量矩阵大小：

\[||A||_ {F} = \sqrt{\sum_ {i,j} A^2_ {i,j} } \]

• 对角矩阵：用\(diag(\boldsymbol{v})\)表示由向量\(\boldsymbol{v}\)构成的对角阵。

  • 对角阵的逆：\(diag(\boldsymbol{v})^{-1}=diag([1/v_ {1},...,1/v_ {n}]^ {T})\)

• 对称矩阵： \(A=A^T\)

• 正交向量：\(x^T y=0\)，如果范数均为1，则称为标准正交。

• 正交矩阵：行向量标准正交，列向量也标准正交。则\(A^T A = A A^T =I\)，这时\(A^{-1}=A^{T}\)。

• 特征向量与特征值：

  满足$$Av=\lambda v$$的\(v\)称为特征向量，\(\lambda\)称为特征值。

  推导：设A有n个线性无关的特征向量，写成矩阵\(V=(v^{(1)} ,...,v^{(n)})\)，对应特征值为
  \((\lambda_1,...,\lambda_n)\)，写成向量\(\boldsymbol{\lambda} = [\lambda_1,...,\lambda_n]^T\)。
  则\(AV = A( v^{(1)} ,...,v^{(n)} ) = ( v^{(1)} ,...,v^{(n)} ) diag(\boldsymbol{\lambda}) = V diag(\boldsymbol{\lambda}) \rightarrow A=V diag(\boldsymbol{\lambda}) V^{-1}\)。这就是A的特征分解。

\[A=V diag(\boldsymbol{\lambda}) V^{-1} \]

\(Av=\lambda v\)的理解如下图：

• 每个实对称矩阵都可以分解为\(A=Q \boldsymbol{\Lambda} Q^{T}\)，其中\(Q\)为A的特征向量组成的正交矩阵，可以将A看作沿方向\(v^{(i)}\)延展\(\lambda_i\)倍的空间。

• 二次方程\(f(x)= x^T Ax\)，其中\(||x||_ {2} =1\)。当\(x\)为某特征向量时，f将返回对应的特征值。

• 正定阵：所有特征值都是正数；如果正定阵A满足\(x^T Ax =0\)，则\(x=0\)。

• 半正定：所有特征值都是非负数；半正定矩阵的\(x^T Ax \geq 0\)

• 奇异值分解(Singluar Value Decomposition, SVD)：类似于\(A=V diag(\boldsymbol{\lambda}) V^{-1}\)，将矩阵A分解为\(A=UDV^{-1}\)，U是\(m \times m\)正交方阵，D是\(m \times n\)对角矩阵，V是\(n \times n\)正交方阵。

  • U的列向量为左奇异向量，是\(AA^T\)的特征向量；
  • V的列向量为右奇异向量，是\(A^T A\)的特征向量；
  • 对角矩阵D的元素为矩阵A的奇异值，是\(AA^T\)特征值的平方根，同时也是\(A^T A\)特征值的平方根。

• Moore-Penrose伪逆：求解\(Ax=y\)时，\(x=A^{-1}y\)，但矩阵A可能没有逆矩阵。伪逆为：

\[A^+ = lim_ {a \rightarrow 0} (A^T A + \alpha I)^{-1} A^T \]

计算时，\(A^+ =VD^+ U^T\)，其中U、D、V时矩阵奇异值分解后得到的矩阵。对角矩阵D的伪逆\(D^+\)是其非零元素取倒数之后再转置得到的。
得到\(x=A^+ y\)。

• 迹：\(Tr(A) = \sum_i A_ {i,i}\)。矩阵A的Frobenius范数的另一种形式\(||A||_ {F} =\sqrt{Tr(AA^T)}\)

  • \(Tr(A)=Tr(A^T)\)
  • \(Tr(ABC)=Tr(CAB)=Tr(BCA)\)
  • \(a=Tr(a)\)

• 行列式：\(det(A)\)为矩阵特征值的乘积。

• 利用上述知识可推导主成分分析(Principal Components Analysis, PCA)的公式。

补充：矩阵求导相关公式

下列\(\boldsymbol{a}\)与\(A\)均为常数组成的向量和矩阵，\(\boldsymbol{x}\)为自变量(向量形式)。请自行推导。

• \[\frac{\partial a^T x}{\partial x}=\frac{\partial x^T a}{\partial x}=a \tag{1} \]

• \[\frac{\partial x^T A}{\partial x}=A \tag{2} \]

• \[\frac{\partial x^T Ax}{\partial x}=(A+A^T)x \tag{3} \]