机器学习实战笔记-8-回归
回归
线性回归
设\(\mathbf{x}^{\mathbf{T}}\)向量第一列全为1，即\(x_{0} = 1\)，这样\(x_{0}w_{0}\)代表的是截距，\(x_{1}w_{1}\)是斜率：
设回归方程\(y_{i}^{'} =\mathbf{x}_{\mathbf{i}}^{T}\mathbf{\omega}\)，则回归的评价指标：误差的平方和\(\sum_{i = 1}^{m}\left( y_{i} - \mathbf{x}_{i}^{T}\mathbf{\omega} \right)^{2}\)，
写作矩阵形式：
回归方程为\(\mathbf{y}' = X\mathbf{\omega}\)，其中\(\mathbf{y}'\)为\(m \times 1\)，\(X\)为\(m \times n\)，误差的平方和\(\delta = \left( \mathbf{y}X\mathbf{\omega} \right)^{T}(\mathbf{y} - X\mathbf{\omega})\)
令\(\frac{\partial\delta}{\partial\mathbf{\omega}} = - X^{T}\mathbf{y+}X^{T}X\mathbf{\omega}\mathbf{= 0}\)，得到回归系数为\(\mathbf{\omega} =\left( \mathbf{X}^{T}\mathbf{X} \right)^{- 1}\mathbf{X}^{T}\mathbf{y}\)
用相关系数corrcoef(yHat.T,yMat)可以计算得到相关系数，即拟合指标。
局部加权线性回归
使用“核”给预测点附近每个点赋予更高的权重，即\(w\left( i,i \right) = \exp\left( \frac{\left| x_{i} - x \right|}{- 2k^{2}} \right)\)。则回归系数
其中\(\mathbf{W}\)是\(w\left( i,i \right)\)形成的矩阵。
-
\(k\)越小，预测点附近的点权重越大，越看重细节。易造成过拟合。过拟合的误差\(\sum_{i = 1}^{m}\left( y_{i} - y_{i}^{'} \right)^{2}\)较小。但预测新数据的效果未必越好。
-
\(k\)越大，预测点附近的点权重越平均，越看重整体。\(k = 1\)时基本与简单线性回归一样了。
缩减系数之岭回归
如果上述训练集的特征比样本点数多(n>m)，输入数据的矩阵不是满秩矩阵，求逆会出现问题。作以下修正即可（其中\(\mathbf{I}\)大小为m*m）：
\( \mathbf{\omega} = \left( \mathbf{X}^{T}\mathbf{X}\mathbf{+}\lambda\mathbf{I} \right)^{- 1}\mathbf{X}^{T}\mathbf{y} \)
数据获取之后，首先抽取部分用于测试，其余用于训练出参数\(\mathbf{\omega}\)，训练完毕后在测试集上测试性能，选取不同的\(\mathbf{\lambda}\)重复上述过程，得到使预测误差最小的\(\mathbf{\lambda}\)。
可知，\(\lambda\)越小(越接近0)，各系数与普通回归一样；随着\(\lambda\)不断增大，系数全部缩减为0。取中间的值可以得到最好的预测效果。
该方法等效于 普通线性回归+约束：\(\sum_{k = 1}^{n}{\omega_{k}^{2} \leq\lambda}\)
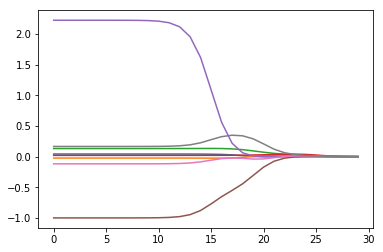
图、 回归系数与\(\lambda\)的关系
- 缩减系数之前向逐步回归：属于贪心算法(每一步都尽可能减小误差)
算法伪代码：每次迭代更改w(中一个特征的一个小值)，以得到做这样改动的最优解。
数据标准化(满足0均值和单位方差：数据减去均值后处以方差)
for 每轮迭代：
设置最前最小误差lowestError为正无穷
对每个特征:
增大或缩小一个系数得到新的w
计算新w下的误差
如果误差Error小于lowestError：设置WBest为当前w
将WBset设置为新的w
缩减系数的目的在于：“理解”特征对回归的作用。
关于矩阵求导：其中\(\mathbf{x,\beta}\)均为列向量。
\( \frac{\partial\mathbf{\beta}^{T}\mathbf{x}}{\partial\mathbf{x}} = \frac{\partial\mathbf{x}^{T}\mathbf{\beta}}{\partial\mathbf{x}} = \mathbf{\beta}() \)
\( \frac{\partial\mathbf{x}^{T}\mathbf{x}}{\partial\mathbf{x}} = 2\mathbf{x}() \)
\( \frac{\partial\mathbf{x}^{T}\mathbf{A}\mathbf{x}}{\partial\mathbf{x}} = \frac{\partial\mathbf{x}^{T}\mathbf{A}^{T}\mathbf{x}}{\partial\mathbf{x}} = \frac{\partial(\mathbf{x}^{T}\mathbf{)}\mathbf{A}\mathbf{x}}{\partial\mathbf{x}}\mathbf{+}\frac{\partial\mathbf{x}^{T}\mathbf{A}\mathbf{(x)}}{\partial\mathbf{x}} = \frac{\partial(\mathbf{x}^{T}\mathbf{A}\mathbf{)x}}{\partial\mathbf{x}}\mathbf{+}\frac{\partial\mathbf{x}^{T}\mathbf{(}\mathbf{A}\mathbf{x)}}{\partial\mathbf{x}} = \mathbf{A}^{T}\mathbf{x} + \mathbf{Ax =}\left( \mathbf{A}^{\mathbf{T}}\mathbf{+ A} \right)\mathbf{x} \)
