大地经纬度坐标系与Web墨卡托坐标系的转换
1. 概述
我在《大地经纬度坐标与地心地固坐标的的转换》这篇文章中已经论述了大地坐标系/地理坐标系的概念，简单来说就是由经度、纬度以及高程（BLH）确定的坐标系，它是一种曲面坐标。
然而，在实际使用过程中我们用的最多的还是平面坐标，并且单位最好与常用的长度单位（米）一致。所以就产生了从曲面到平面的转换，这个过程也叫做投影，转换的结果也就是投影平面坐标系。我在《GDAL坐标转换》这篇文章中详细论述了我们国内常用的三种投影平面坐标系：横轴墨卡托投影，高斯-克吕格投影和UTM投影。本质上来说，高斯-克吕格投影和UTM投影其实都是横轴墨卡托投影，横轴墨卡托投影也是用的最为广泛的地图投影方式。
但是在GIS，尤其是WebGIS领域中，横轴墨卡托投影的使用远没有Web墨卡托投影方式用的多。最重要的原因是Web墨卡托投影的转换算法比横轴墨卡托投影要简单很多，符合Web的轻量化的特点。
2. 实现
Web墨卡托投影是横轴墨卡托投影的特化版，要完全搞清楚Web墨卡托投影就必须得先搞清楚横轴墨卡托投影，不过横轴墨卡托投影实在太复杂了，但是我们可以定性地去理解。它的计算过程大概可以这样理解：
在X方向上，为了保证投影到平面后经线和纬线仍然垂直，那么每条纬线都会按照赤道周长展开，也就是\(2*PI*r = 2*20037508.3427892\)。由于原点位于平面中心，那么可以算得X轴的取值范围：[-20037508.3427892,20037508.3427892]。经度与投影后X长是简单的线性关系。
在Y方向上，则需要借助于墨卡托投影公式。为了保证投影的结果是正方形，那么就把Y轴的取值范围也取值成[-20037508.3427892,20037508.3427892]之间。这样做没什么道理，纯粹是为了希望投影的结果是正方形，便于切片。最后，通过墨卡托投影公式进行反算，得到的经纬度范围就是[-85.05112877980659，85.05112877980659]。也就是这种投影方式，大于这个范围是失效的。
参考Cesium的具体实现如下：
#include <iostream>
//#include <eigen3/Eigen/Eigen>
//#include <osgEarth/GeoData>
using namespace std;
const double epsilon = 0.000000000000001;
const double pi = 3.14159265358979323846;
const double d2r = pi / 180;
const double r2d = 180 / pi;
const double a = 6378137.0; //椭球长半轴
const double f_inverse = 298.257223563; //扁率倒数
const double b = a - a / f_inverse;
//const double b = 6356752.314245; //椭球短半轴
const double e = sqrt(a * a - b * b) / a;
//墨卡托范围[-PI, PI]->大地纬度范围[-PI/2, PI/2]
static double mercatorAngleToGeodeticLatitude(double mercatorAngle)
{
return pi / 2.0 - (2.0 * atan(exp(-mercatorAngle)));
//return 2.0 * atan(exp(mercatorAngle)) - pi / 2.0;
}
//Web墨卡托投影所支持的最大纬度（北和南）
static double maximumLatitude = mercatorAngleToGeodeticLatitude(pi);
//大地纬度范围[-PI/2, PI/2]->墨卡托范围[-PI, PI]
static double geodeticLatitudeToMercatorAngle(double latitude)
{
// Clamp the latitude coordinate to the valid Mercator bounds.
if (latitude > maximumLatitude)
{
latitude = maximumLatitude;
}
else if (latitude < -maximumLatitude)
{
latitude = -maximumLatitude;
}
double sinLatitude = sin(latitude);
return 0.5 * log((1.0 + sinLatitude) / (1.0 - sinLatitude));
}
void Blh2Wmc(double &x, double &y, double &z)
{
x = x * d2r * a;
y = geodeticLatitudeToMercatorAngle(y * d2r) * a;
}
void Wmc2Blh(double &x, double &y, double &z)
{
//var oneOverEarthSemimajorAxis = this._oneOverSemimajorAxis;
x = x / a * r2d;
y = mercatorAngleToGeodeticLatitude(y / a) * r2d;
}
int main()
{
double x = 113.6;
double y = 38.8;
double z = 100;
printf("%.10lf\n", maximumLatitude * r2d);
printf("原大地经纬度坐标：%.10lf\t%.10lf\t%.10lf\n", x, y, z);
Blh2Wmc(x, y, z);
printf("Web墨卡托坐标：%.10lf\t%.10lf\t%.10lf\n", x, y, z);
Wmc2Blh(x, y, z);
printf("转回大地经纬度坐标：%.10lf\t%.10lf\t%.10lf\n", x, y, z);
}
最终运行的结果：
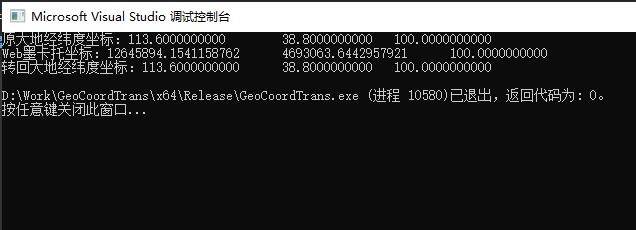
通过GlobalMapper中的坐标转换工具对照的结果如下：
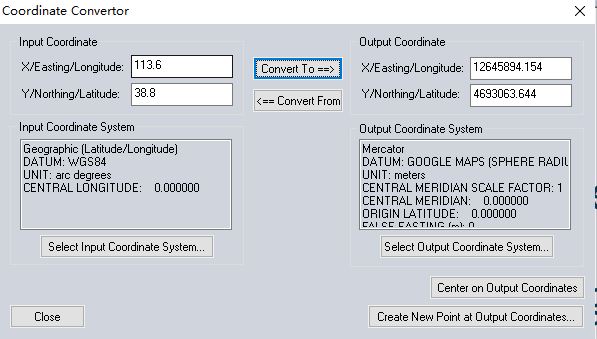
两者结果基本一致。
