P9527 [JOISC2022] 洒水器 题解
以下设 \(\operatorname{dis}(x,y)\) 表示树上 \(x,y\) 两点间的距离。修改时对 \(u\) 的周围与 \(u\) 距离小于等于 \(d\) 的点的点权乘 \(w\)。
暴力不行，于是考虑打标记。
注意到 \(0\le d\le 40\)，一个很自然的想法是：设 \(tag(x,i)\) 表示将 \(x\) 的子树内与 \(x\) 距离小于等于 \(i\) 的所有点的点权乘 \(tag(x,i)\)。修改时遍历 \(l\) 分别表示 \(u\)、\(u\) 的父亲……\(u\) 的 \(d\) 级祖先，将 \(tag(l,d-\operatorname{dis}(u,l))\) 都乘上 \(w\) 即可。查询时依然遍历 \(l\)，沿途把标记累乘即可。这样 \(l\) 最多 \(O(d)\) 个取值，总时间复杂度是 \(O(nd)\) 的。
显然这样会有点权被重复乘 \(w\)，解决方案也很简单，打标记时将重复的用除法抵消。具体的，设 \(l\) 的一个孩子 \(s\)，使 \(s\) 的子树内有 \(u\)，打标记时将 \(tag(s,d-\operatorname{dis}(u,l)-1)\) 即 \(tag(s,d-\operatorname{dis}(u,s)-2)\) 除以 \(w\) 即可。
下图给出了一个例子帮助理解：
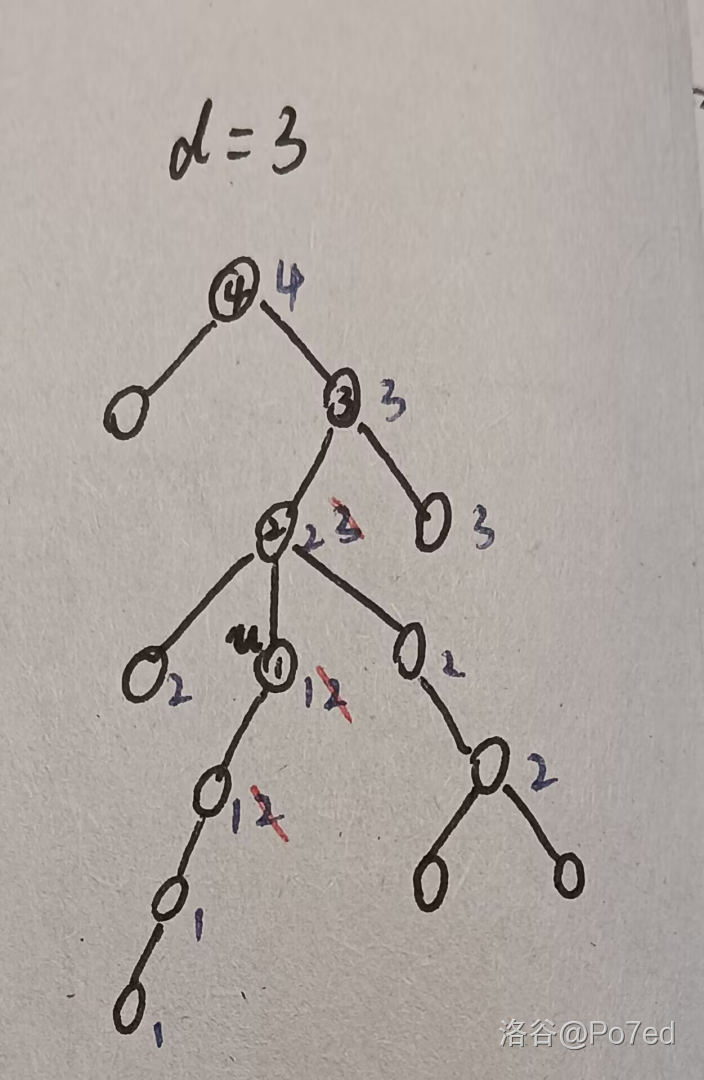
图中 \(1\) 号点（即 \(u\)）将它自己和它下面的 \(3\) 个点乘了 \(w\)，\(2\) 号点也将其子树内的 \(5\) 个点乘 \(w\)，但 \(1\) 号点由于被重复乘，通过除法被消去了一次。同理，\(3\) 号乘了 \(3\) 个点，其中 \(2\) 号点被消去了一次。\(4\) 号乘了它自己。这样每个需要乘的点都刚好被乘了一次。
但模数可能没有逆元，这样做还是不行。
不妨换个角度，观察到 \(l\) 可以取到 \(s\)，即对于 \(s\) 的标记的操作，事实上是 \(tag(s,d-\operatorname{dis}(u,s))\) 乘 \(w\)，\(tag(s,d-\operatorname{dis}(u,s)-2)\) 除以 \(w\)。
考虑对标记的定义稍作修改，设 \(tag'(x,i)\) 表示将 \(x\) 的子树内与 \(x\) 距离刚好等于 \(i\) 的所有点的点权乘 \(tag'(x,i)\)，则上面对 \(s\) 的标记的操作等价于 \(tag'(s,d-\operatorname{dis}(u,s)-1)\) 和 \(tag'(s,d-\operatorname{dis}(u,s))\) 都乘 \(w\)。我们成功地将一乘一除转化为了两个乘。（有点类似前缀和的还原。）对应到上图的例子，就是换一个乘 \(w\) 消：
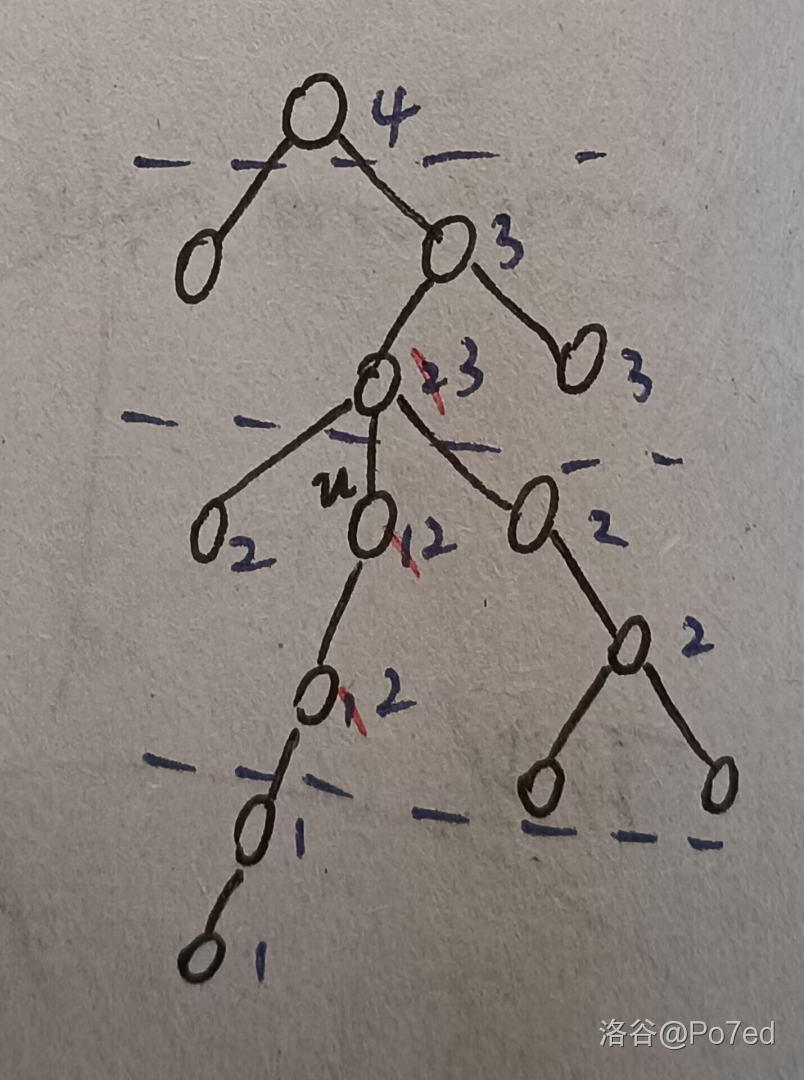
这样，时间复杂度依然是 \(O(nd)\) 的，询问时还是直接跳祖先乘标记。
代码：
#include <iostream>
#include <vector>
const int N=214514,D=100;
int n,m,mod;
int a[N];
int tag[N][D],fa[N];
std::vector<int> e[N];
void dfs(int u,int f=0)
{
fa[u]=f;
for(int v:e[u])if(v!=f)dfs(v,u);
}
int main()
{
scanf("%d %d",&n,&mod);
int u,v;
for(int i=1;i<n;i++)
{
scanf("%d %d",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
dfs(1);
for(int i=1;i<=n;i++)scanf("%d",a+i);
for(int i=1;i<=n;i++)for(int j=0;j<=40;j++)tag[i][j]=1;
scanf("%d",&m);
int o,x,d,w;
while(m--)
{
scanf("%d %d",&o,&x);
if(o==1)
{
scanf("%d %d",&d,&w);
while(d>=0&&x)
{
tag[x][d]=1ll*tag[x][d]*w%mod;
if(d>=1)tag[x][d-1]=1ll*tag[x][d-1]*w%mod;
if(x==1) // 根节点要特判，因为根节点没有祖先抵消
{
for(int i=0;i<=d-2;i++)tag[1][i]=1ll*tag[1][i]*w%mod;
break;
}
x=fa[x];
d--;
}
}
else
{
int ans=a[x];
for(d=0;d<=40;d++) // 跳父亲累乘 tag
{
if(!x)break;
ans=1ll*ans*tag[x][d]%mod;
x=fa[x];
}
printf("%d\n",ans);
}
}
return 0;
}
