CF1833G Ksyusha and Chinchilla 题解

题目传送门

题意简介

在一棵树上删去一些边，使得形成的几个连通块，都有且仅有 $3$ 个结点。

多个答案时仅需输出任意一个。

每个测试点有多组测试数据。

解法

思路

首先注意到每个连通块都有且仅有 $3$ 个结点，所以节点数 $n$ 必须是 $3$ 的倍数。可以先特判。

考虑有解时，我们可以从下往上进行断边操作，可用 dfs 实现。 具体见 算法流程。

算法流程

• 记 $siz_i$ 为当前节点的子树中未被切断为单独的连通快的节点个数（有点绕）。换句话说，不经过断开的边所能到达的子树中的节点的个数。如下图，红色边为应断开的边，

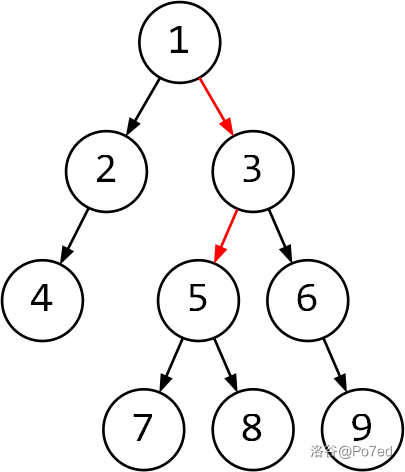
$i$	$1$	$2$	$3$	$4$	$5$	$6$	$7$	$8$	$9$
$siz_i$	$3$	$2$	$3$	$1$	$3$	$2$	$1$	$1$	$1$

可以自行理解一下。

• 计算 $siz_i$：将各个调用的返回值累加。
• $siz_i$ 可分以下情况：（记 $pre$ 为 $i$ 的父亲。）
  • 当 $siz_i=3$ 时，断开边 $(i,pre)$。同时返回 $0$ 表示没有未被切断的节点（都被切断了）。
  • 当 $siz_i<3$ 时，还不够一个连通块的节点数量 $3$，所以返回 $siz_i$。
  • 当 $siz_i>3$ 时，节点数量太多，输出 $\texttt{-1}$，结束。
• 返回到主函数后，若返回值为 $0$，则有解，输出解。否则输出 $\texttt{-1}$，结束。

代码

#include <iostream>
#include <vector>
using namespace std;

struct edge
{
    int v,id;
};

vector<edge> del;//记录删除的边
vector<edge> e[200001];//边表

int dfs(int now,int pre)
{
    int siz=1;
    edge tofa;
    for(edge to:e[now])//遍历所有连边
    {
        if(to.v!=pre)
        {
            siz+=dfs(to.v,now);//累加返回值
        }
        else
        {
            tofa=to;//标记与父亲连的边
        }
    }
    if(siz==3)//判断siz
    {
        if(pre!=-1)//特判，如果是根节点（1号），它没有父亲，不能删除与父亲连的边，不然会出错
        {
            del.push_back(tofa);
        }
        return 0;
    }
    else if(siz<3)
    {
        return siz;
    }
    else
    {
        // puts("-1");不能直接输出-1，因为不能退出程序，也无法直接回到main函数
        return 0x3f3f3f3f;//让返回值极大，导致在主函数的特判中判定为无解
    }
    return 114514;//没用的，只是为了让编译器不报错
}

int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        del.clear();//清除上一次的记录
        // fill(vtoid,vtoid+n+1,0);
        int n;
        scanf("%d",&n);
        int u,v;
        if(n%3)
        {
            puts("-1");
            for(int i=1;i<n;i++)
            {
                scanf("%d %d",&u,&v);
            }
            continue;
        }
        for(int i=1;i<=n;i++)
        {
            e[i].clear();
        }
        for(int i=1;i<n;i++)
        {
            scanf("%d %d",&u,&v);
            e[u].push_back({v,i});
            e[v].push_back({u,i});
        }
        if(!dfs(1,-1))//特判，如果返回值为0，则完美分配了所有节点。反之没有，就无解。
        {
            printf("%d\n",del.size());
            for(edge d:del)
            {
                printf("%d ",d.id);
            }
            puts("");
        }
        else
        {
            puts("-1");
        }
    }
    return 0;
}