扫描线

前言

扫描线可以配合线段树解决矩形面积并、周长并的问题。

先上张 OI Wiki 的图：

这张动图是从下扫到上，本文将以从左扫到右的顺序实现。

扫描线

看完上面那张动图，相信你已经对扫描线有了初步认识。

为了匹配解说，我把图魔改了一下。

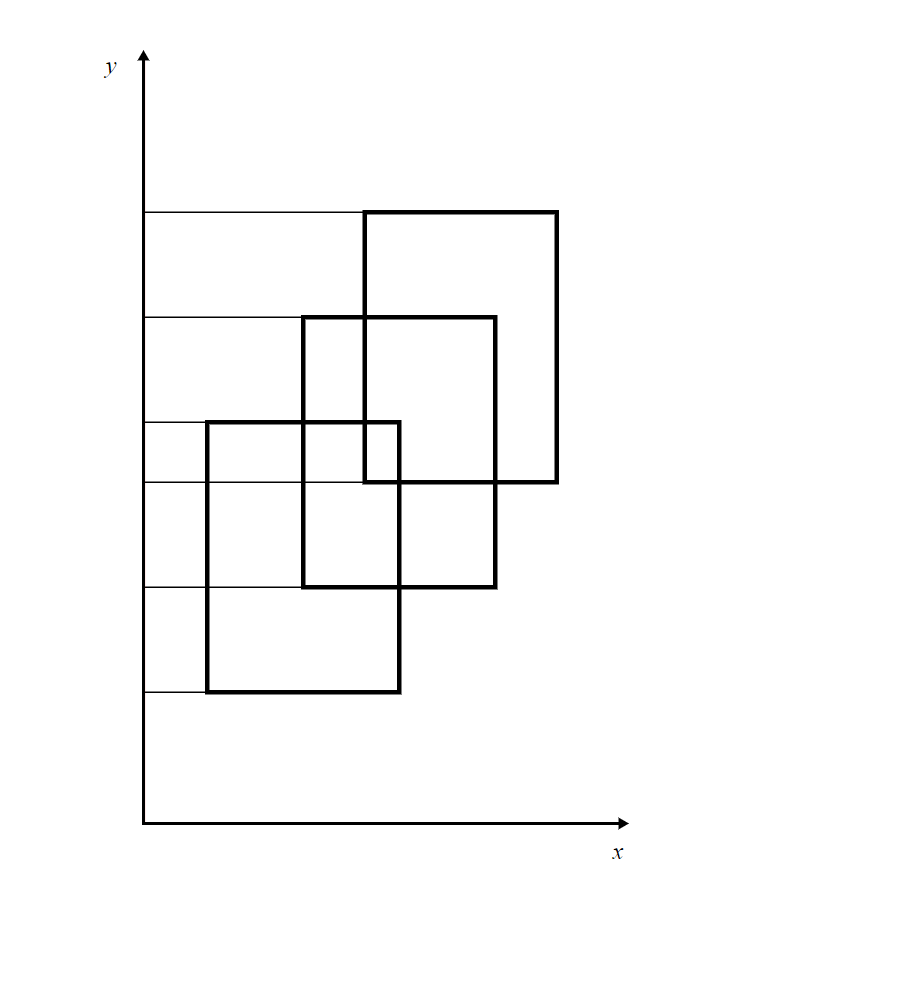
现在我们想象一根线从左往右扫过图形，图中它会与所有纵边重合。

我们给它们赋上边权，如图，蓝色边权值为 \(1\)，红色为 \(-1\)：

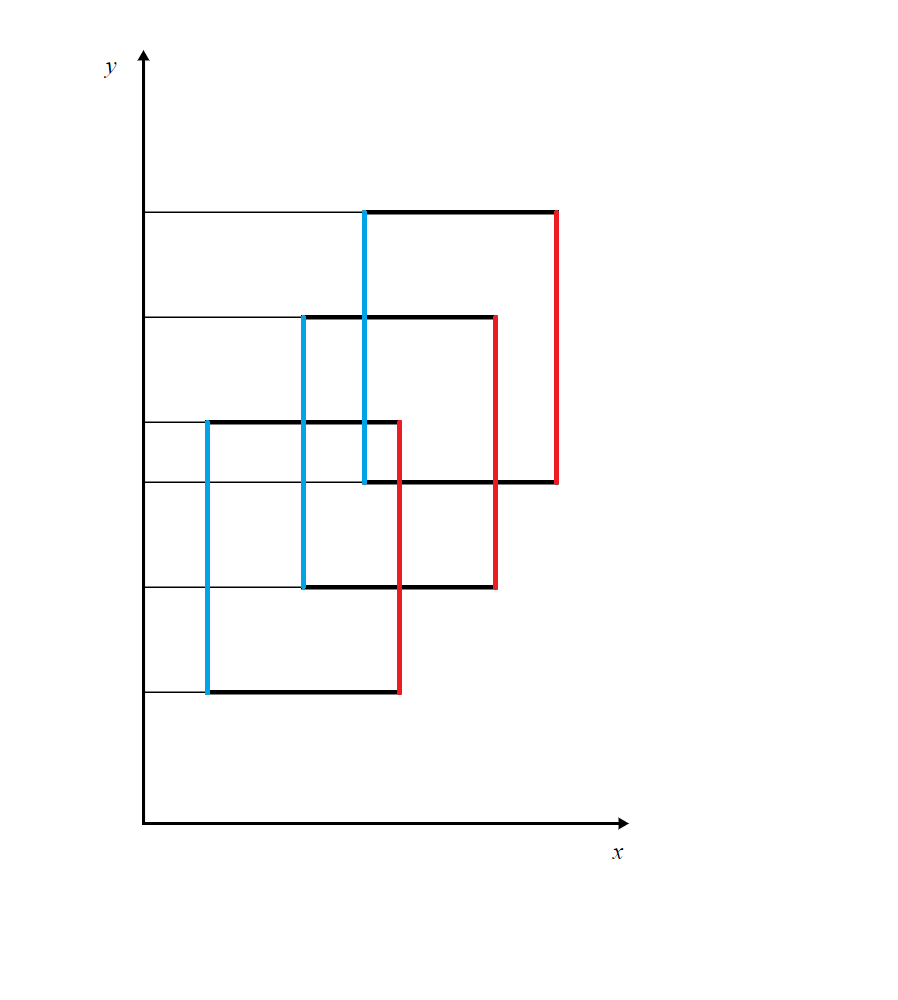
显然每个矩形中扫描线先扫到的纵边就是蓝边，否则为红边。

紧接着像图中那样，全部纵坐标在 \(y\) 轴上截出 \(5\) 条线段。

我们把对这 \(5\) 条线段建立线段树，当扫描线扫过一条纵边时，就将纵边所对应的所有 \(y\) 轴上的线段进行区间修改（\(\pm 1\)）。这个过程可以看文首的动图，一眼就懂，清晰明了。注意 \(x\) 轴下方的数字！

每次扫描线碰到纵边，就进行区间修改。然后我们查询线段树中当前的总长（紫色） \(\times\) 当前纵边和下一条纵边的距离（蓝色），再累加，就得到了总面积。如图：

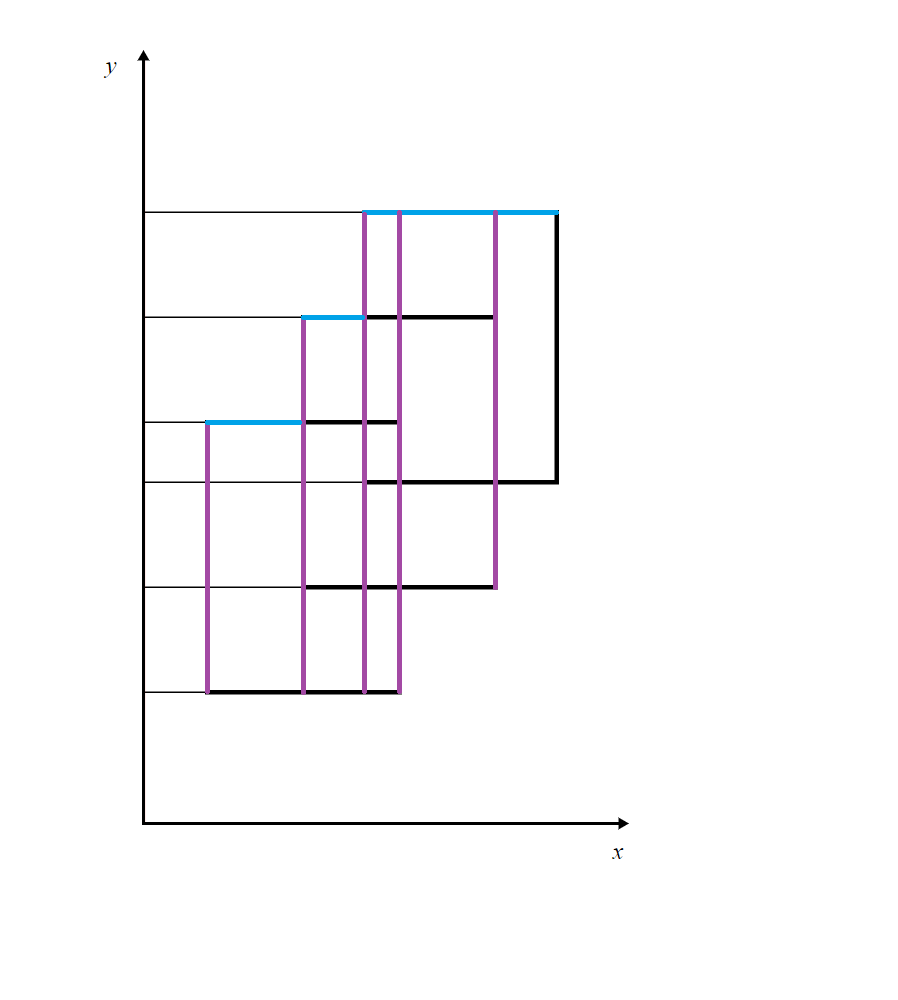
Q：注意到动图中有些线段的 \(cnt\) 算了多次，怎么去重？
A：通过线段树特殊的合并方式。具体可以看代码。

代码

#include <iostream>
#include <vector>
#include <algorithm>

typedef long long ll;
constexpr int N=114514;
int n,m;

struct seg{int x,y1,y2,v;};// 存纵边的 struct
seg s[N<<1];
int y[N<<1];// 存所有出现过的 y 值

namespace sgt// 建议先看 main()
{
	struct node{int sum,len;node():sum(0),len(0){}};// 线段树的节点
	//                      ^~~~~~~~~~~~~~~~~~~~~~ 这是默认构造函数（默认初始化值）
	// 注意每个节点表示一条线段
	// 保存两个值：sum（即动图中的 cnt，但对于非叶子节点，sum 表示一整条线段而非一部分的累加次数）
	// len：当前线段中被取了的部分的长度
	// 以上两个变量不理解可以结合下面的函数理解
	node t[N<<4];
	#define ls (pos<<1)
	#define rs (pos<<1|1)
	#define mid ((l+r)>>1)
	// 以下 pos 为线段树内节点编号，l 为线段树内左端点，r 右端点
	inline void update(int pos=1,int l=1,int r=m-1)// 注意这里是 m-1，因为 m 个不同的 y 值只截出了 m-1 条线段（可以结合图理解）
	{// 特殊的合并方式
		if(t[pos].sum)t[pos].len=y[r+1]-y[l];// 如果这一整条线段被取过，那么被取过的长度即为整条线段的长度
		else t[pos].len=t[ls].len+t[rs].len;// 否则需要合并左右儿子的长度
	}
	//        新增线段的位置；类型（1/-1）
	void modify(int yl,int yr,int v,int pos=1,int l=1,int r=m-1)
	{
		if(yl<=y[l]&&y[r+1]<=yr)return t[pos].sum+=v,update(pos,l,r);// 如果完全包含整条线段，直接加出现次数，并更新
		if(yl<y[mid+1])modify(yl,yr,v,ls,l,mid);// 如果修改区间涵盖了左儿子，修改
		if(y[mid+1]<yr)modify(yl,yr,v,rs,mid+1,r);// 同理
		update(pos,l,r);// 记得更新
	}
} // namespace sgt


int main()
{
	scanf("%d",&n);
	int x1,y1,x2,y2;
	for(int i=1;i<=n;i++)// 输入每个矩形
	{
		scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
		s[i]={x1,y1,y2,1};// 保存两条纵边
		s[i+n]={x2,y1,y2,-1};
		y[i]=y1,y[i+n]=y2;// 保存所有出现过的 y 值
	}
	n<<=1;// 方便处理
	std::sort(s+1,s+n+1,[](seg a,seg b)->bool {return a.x<b.x;});// 对所有纵边按 x 坐标排序（从左到右）
	std::sort(y+1,y+n+1);// 离散化
	m=std::unique(y+1,y+n+1)-y-1;// 共 m 个不同的 y
	ll ans=0;
	for(int i=1;i<n;i++)// 从左到右扫过每条纵边
	{
		sgt::modify(s[i].y1,s[i].y2,s[i].v);// 标记出现
		ans+=1ll*sgt::t[1].len*(s[i+1].x-s[i].x);// 计算面积，累加
	}
	printf("%lld",ans);
	return 0;
}