10/25

今日考题
1.说说截至目前你所知道的算法模型以及各自你所知道的特点

1.一元线性回归模型
	即一个变量对结果产生影响的情况
    只有一个自变量和多个应变量
    最后的数学在坐标中是直线
    # 哑变量
    通过类似矩阵表达出非数字的数据
2.多元线性回归模型
	较于前者自变量可以有多个
    更贴进生活 多变量组合影响结果
    最后的数学图像是抛物线
'''线性回归短板:
1.自变量之间不能有联系
2.自变量个不能大于样本量'''
3.岭回归模型
	用于解决线性回归中模型不准的情况
    从而添加了一个惩罚项(平方项)
    经数学处理之后变成 一个抛物线(圆锥)和圆(球)
    最后结果即变成了求两图形交点的过程
    # 交叉验证
    多次进行训练集和测试集的分组 最后取用最优解
    Lasso也用
4.Lasso回归
	用于结果变量有不合理的情况 
    同样通过添加惩罚项(绝对值项)来解决
    经数学公式转换之后会变成求菱形(菱形底面的六面体)与抛物线(圆锥)交点问题
    而且降低了模型复杂度
5.Logistic模型
	对线性回归模型做logit数学转化之后能将线性模型变成logistic模型
    图像是一个最小值无限趋近0 最大值无限趋近1的图案
    从而将回归模型中的预测值变成一个百分比的预测
# ROC曲线与KS曲线
	通过绘制图形来观察模型是否合理
6.决策树
	从根条件开始分叉出别的条件和结果
    就像是个倒过来的树一样展开
    最后的结果是叶子节点 开始的地方是根节点
    别的都算中间节点(枝节点)
    一般对结果影响越大越靠近根节点
    但是由于出现频率越高对结果影响必然越大所以要乘以一个与出现次数呈反比的系数基尼指数 来作为信息增益率的限制
# 随机森林
就是由多个决策树组成 其中决策树尽可能多的细分并且无所谓节点顺序
最后通过投票法 获取最优的模型
8.K近邻模型
	通过观察周围一定范围内的数据来确认位置区域的数据
    一定距离K在选取的时候需要 结果准确率尽可能高 MSE尽可能小
    且在K范围内 距离所需数据越近的对所需数据影响越大
    

复习巩固

• 线性回归
• 岭回归与Lasso回归
• Logistic模型
• 决策树与随机森林
• K近邻模型

内容概要

• 贝叶斯模型
• SVM模型
• K均值模型
• DBSCAN聚类
• linux操作系统

详细讲解

算法

算法其实就是研究问题的解决方法 
    ps:算法工程师就是在研究解决某个问题的最优方法
        一般在计算机中就会转换成逻辑问题和数学问题
        逻辑问题最后又都会转换成数学问题

贝叶斯模型

'''通过已知数据计算出概率 
然后用贝叶斯公式测算
得到未知数据的产生结果的概率'''

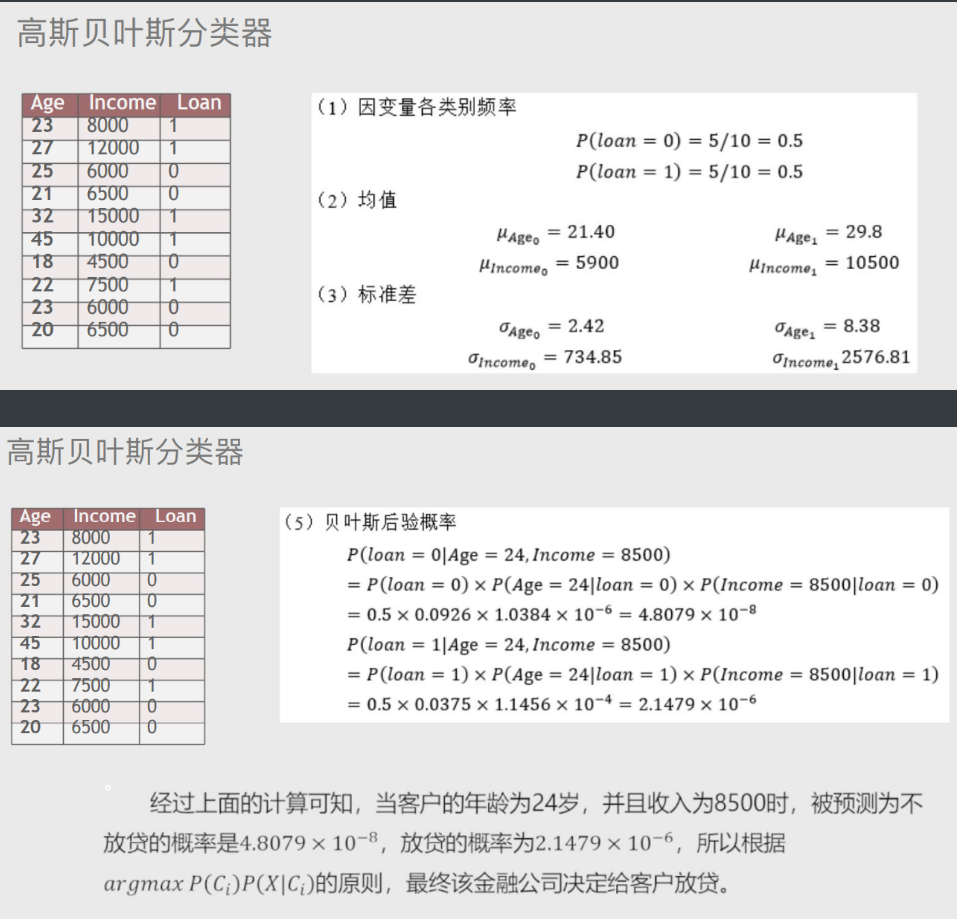
# 高斯贝叶斯分类器
适用于自变量为连续的数值类型的情况

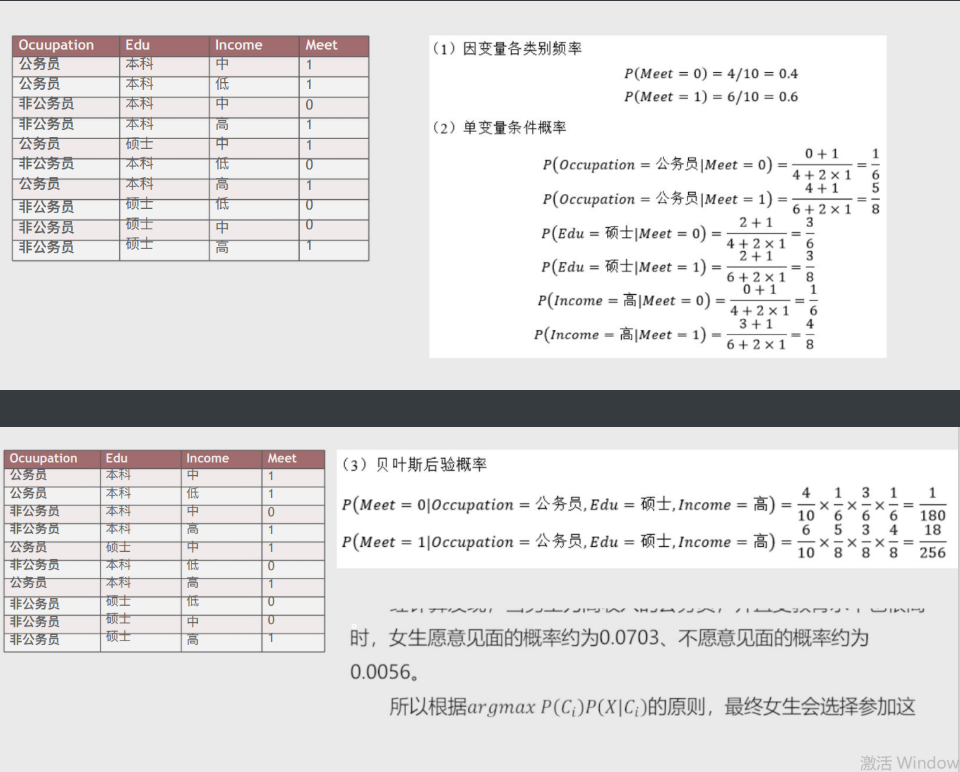
# 多项式贝叶斯分类器
适用于自变量为离散型类型(非数据)

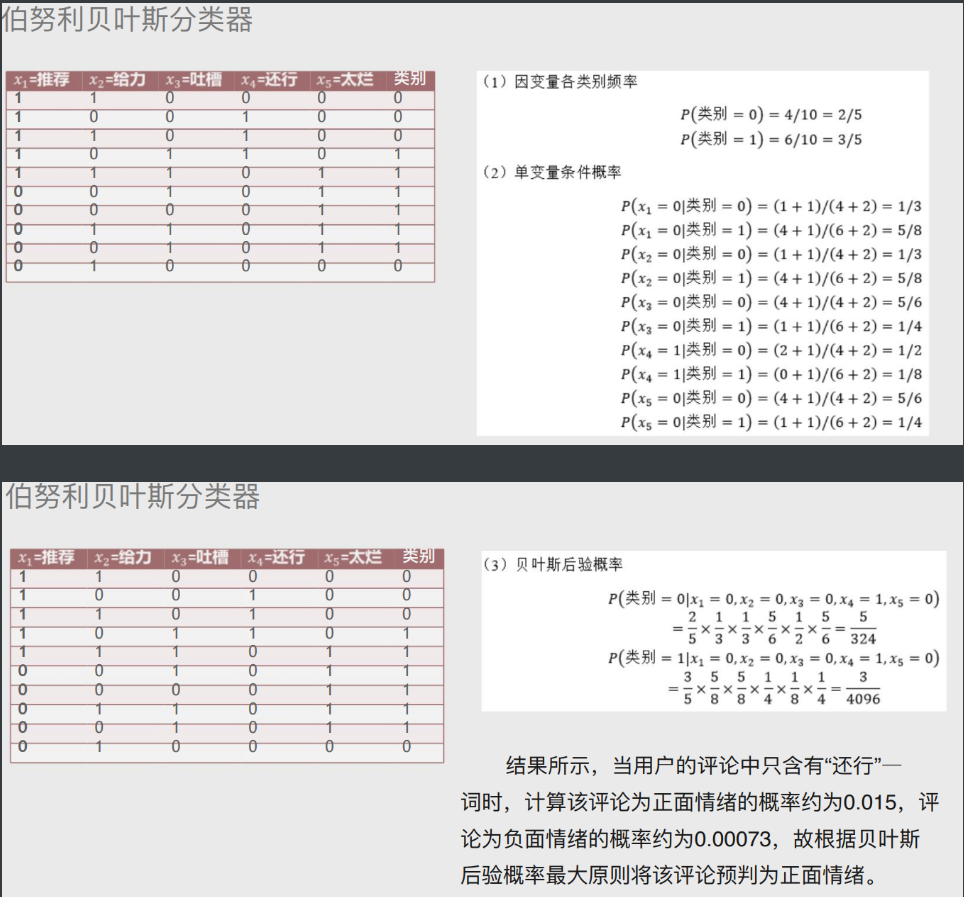
# 伯努利贝叶斯分类器
适用于自变量为二元值的时候(只有两种情况)

实战代码

# 导入第三方包
import pandas as pd
# 读入数据
skin = pd.read_excel(r'Skin_Segment.xlsx')
skin
# 设置正例和负例
skin.y = skin.y.map({2:0,1:1})  # 设置一个映射关系，将2映射成0
skin.y.value_counts()
# 看一眼skin
skin
# 导入第三方模块
from sklearn import model_selection
# 样本拆分
X_train,X_test,y_train,y_test = model_selection.train_test_split(skin.iloc[:,:3], skin.y, 
test_size = 0.25, random_state=1234)
# 导入第三方模块
from sklearn import naive_bayes
# 调用高斯朴素贝叶斯分类器的“类”
gnb = naive_bayes.GaussianNB()
# 模型拟合
gnb.fit(X_train, y_train)
# 模型在测试数据集上的预测
gnb_pred = gnb.predict(X_test)
# 各类别的预测数量
pd.Series(gnb_pred).value_counts()
# 导入第三方包
from sklearn import metrics
import matplotlib.pyplot as plt
import seaborn as sns
# 构建混淆矩阵
cm = pd.crosstab(gnb_pred,y_test)
# 绘制混淆矩阵图
sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd')
# 去除x轴和y轴标签
plt.xlabel('Real')
plt.ylabel('Predict')
# 显示图形
plt.show()

print('模型的准确率为：\n',metrics.accuracy_score(y_test, gnb_pred))
print('模型的评估报告：\n',metrics.classification_report(y_test, gnb_pred))
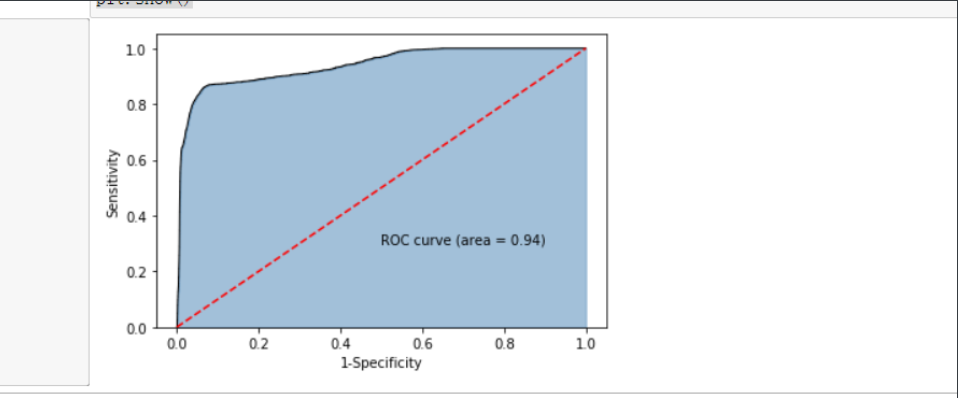
# 计算正例的预测概率，用于生成ROC曲线的数据
y_score = gnb.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)

# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

案例2

# 导入第三方包
import pandas as pd
# 读取数据
mushrooms = pd.read_csv(r'mushrooms.csv')
# 数据的前5行
mushrooms.head()
##################################################################
# 将字符型数据作因子化处理，将其转换为整数型数据
columns = mushrooms.columns[1:]
for column in columns:
    mushrooms[column] = pd.factorize(mushrooms[column])[0]
mushrooms.head()
##################################################################
from sklearn import model_selection
# 将数据集拆分为训练集合测试集
Predictors = mushrooms.columns[1:]
X_train,X_test,y_train,y_test = model_selection.train_test_split(mushrooms[Predictors], mushrooms['type'], 
test_size = 0.25, random_state = 10)
from sklearn import naive_bayes
from sklearn import metrics
import seaborn as sns
import matplotlib.pyplot as plt
# 构建多项式贝叶斯分类器的“类”
mnb = naive_bayes.MultinomialNB()
# 基于训练数据集的拟合
mnb.fit(X_train, y_train)
# 基于测试数据集的预测
mnb_pred = mnb.predict(X_test)
# 构建混淆矩阵
cm = pd.crosstab(mnb_pred,y_test)
# 绘制混淆矩阵图
sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd')
# 去除x轴和y轴标签
plt.xlabel('Real')
plt.ylabel('Predict')
# 显示图形
plt.show()

# 模型的预测准确率
print('模型的准确率为：\n',metrics.accuracy_score(y_test, mnb_pred))
print('模型的评估报告：\n',metrics.classification_report(y_test, mnb_pred))
from sklearn import metrics
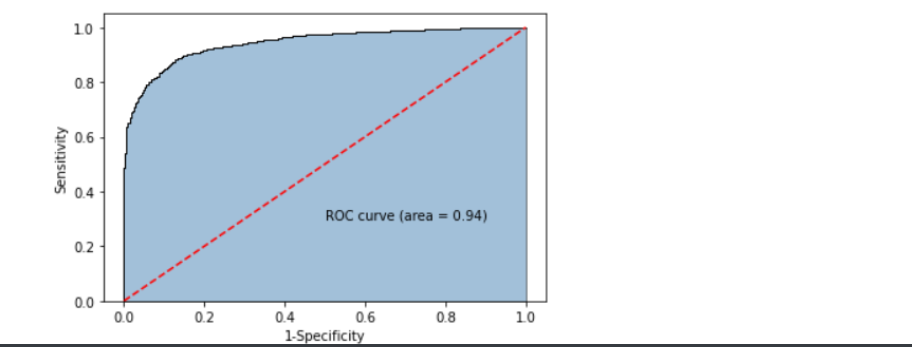
# 计算正例的预测概率，用于生成ROC曲线的数据
y_score = mnb.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test.map({'edible':0,'poisonous':1}), y_score)


# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)

# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

案例3

import pandas as pd
# 读入评论数据
evaluation = pd.read_excel(r'Contents.xlsx',sheet_name=0)
# 查看数据前10行
evaluation.head(10)
# 运用正则表达式，将评论中的数字和英文去除
evaluation.Content = evaluation.Content.str.replace('[0-9a-zA-Z]','')
evaluation.head()

# !pip3 install jieba
# !pip install jieba
# 导入第三方包
import jieba

# 加载自定义词库
jieba.load_userdict(r'all_words.txt')

# 读入停止词
with open(r'mystopwords.txt', encoding='UTF-8') as words:
    stop_words = [i.strip() for i in words.readlines()]

# 构造切词的自定义函数，并在切词过程中删除停止词
def cut_word(sentence):
    words = [i for i in jieba.lcut(sentence) if i not in stop_words]
    # 切完的词用空格隔开
    result = ' '.join(words)
    return(result)
# 对评论内容进行批量切词
words = evaluation.Content.apply(cut_word)
# 前5行内容的切词效果
words[:5]
# 导入第三方包
from sklearn.feature_extraction.text import CountVectorizer
# 计算每个词在各评论内容中的次数，并将稀疏度为99%以上的词删除
counts = CountVectorizer(min_df = 0.01)
# 文档词条矩阵
dtm_counts = counts.fit_transform(words).toarray()
# 矩阵的列名称
columns = counts.get_feature_names()
# 将矩阵转换为数据框--即X变量
X = pd.DataFrame(dtm_counts, columns=columns)
# 情感标签变量
y = evaluation.Type
X.head()
from sklearn import model_selection
from sklearn import naive_bayes
from sklearn import metrics
import matplotlib.pyplot as plt
import seaborn as sns
# 将数据集拆分为训练集和测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size = 0.25, random_state=1)
# 构建伯努利贝叶斯分类器
bnb = naive_bayes.BernoulliNB()
# 模型在训练数据集上的拟合
bnb.fit(X_train,y_train)
# 模型在测试数据集上的预测
bnb_pred = bnb.predict(X_test)
# 构建混淆矩阵
cm = pd.crosstab(bnb_pred,y_test)
# 绘制混淆矩阵图
sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd')
# 去除x轴和y轴标签
plt.xlabel('Real')
plt.ylabel('Predict')
# 显示图形
plt.show()

# 模型的预测准确率
print('模型的准确率为：\n',metrics.accuracy_score(y_test, bnb_pred))
print('模型的评估报告：\n',metrics.classification_report(y_test, bnb_pred))
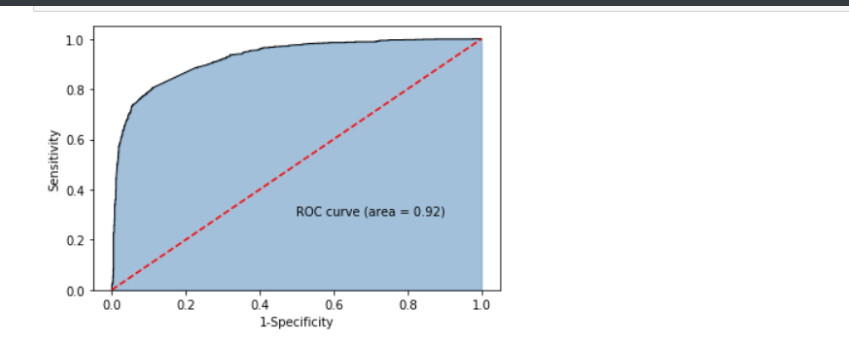
# 计算正例Positive所对应的概率，用于生成ROC曲线的数据
y_score = bnb.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test.map({'Negative':0,'Positive':1}), y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)

# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

SVM模型

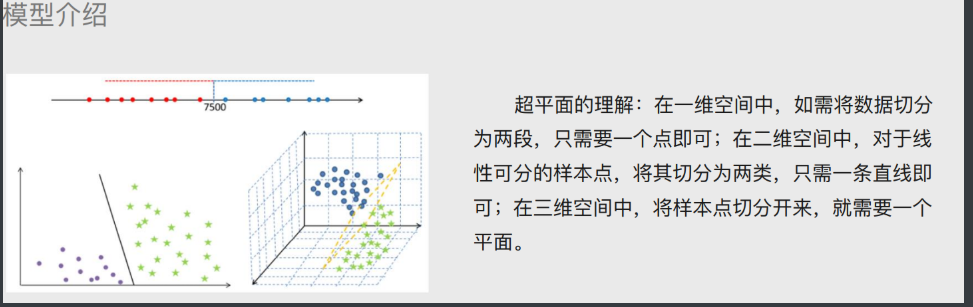
# 超平面概念
将样本点划分成不同的类别(三种表现形式:点、线、面)

# 超平面最优解
1.先随机选择一条直线
2.分别计算两边距离改直线最短的点距离 取更小的距离
3.以该距离左右两边做分隔带
4.依次直线上述三个步骤得出N多个分隔带 最优的就是分隔带最宽的

# 线性可分 与非线性可分
线性可分:简单的理解为就是一条直线划分类别
非线性可分:一条直线无法直接划分 需要升一个维度在做划分
"""常用核函数:高斯核函数>>>>支持无穷维"""

补充

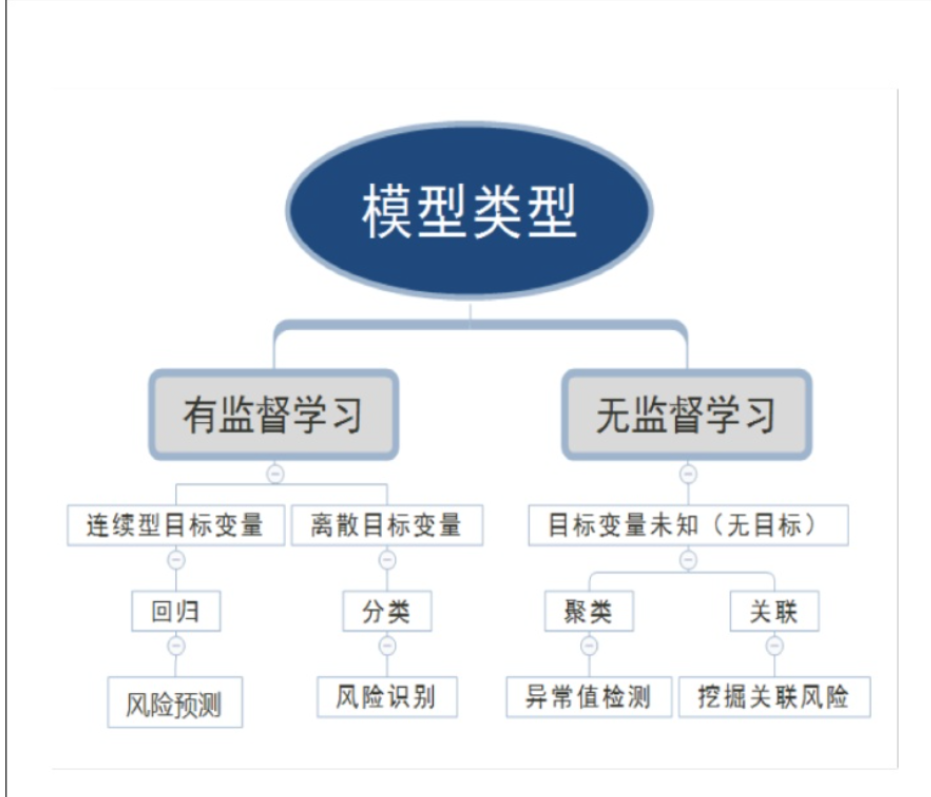
# 有监督学习  
有监督就是有明确需要研究的应变量Y
	输入变量与输出变量均为连续的变量的预测问题称为回归问题(Regression)，输出变量为有限个离散变量的预测问题称为分类问题(Classfication)，输入变量与输出变量均为变量序列的预测问题称为标注问题。
# 无监督学习
后面几个所学的模型就属于无监督学习

SVM代码

# 导入第三方模块
from sklearn import svm
import pandas as pd
from sklearn import model_selection
from sklearn import metrics
# 读取外部数据
letters = pd.read_csv(r'letterdata.csv')
# 数据前5行
letters.head()
# 将数据拆分为训练集和测试集
predictors = letters.columns[1:]
X_train,X_test,y_train,y_test = model_selection.train_test_split(letters[predictors], letters.letter, 
test_size = 0.25, random_state = 1234)
# 选择线性可分SVM模型
linear_svc = svm.LinearSVC()
# 模型在训练数据集上的拟合
linear_svc.fit(X_train,y_train)
# 模型在测试集上的预测
pred_linear_svc = linear_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test, pred_linear_svc)
# 选择非线性SVM模型
nolinear_svc = svm.SVC(kernel='rbf')
# 模型在训练数据集上的拟合
nolinear_svc.fit(X_train,y_train)
# 模型在测试集上的预测
pred_svc = nolinear_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test,pred_svc)

SVM案例2

# 读取外部数据
forestfires = pd.read_csv(r'forestfires.csv')
# 数据前5行
forestfires.head()
# 删除day变量
forestfires.drop('day',axis = 1, inplace = True)
# 将月份作数值化处理
forestfires.month = pd.factorize(forestfires.month)[0]
# 预览数据前5行
forestfires.head()
# 导入第三方模块
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import norm
# 绘制森林烧毁面积的直方图
sns.distplot(forestfires.area, bins = 50, kde = True, fit = norm, hist_kws = {'color':'steelblue'}, 
             kde_kws = {'color':'red', 'label':'Kernel Density'}, 
             fit_kws = {'color':'black','label':'Nomal', 'linestyle':'--'})
# 显示图例
plt.legend()
# 显示图形
plt.show()
# 导入第三方模块
from sklearn import preprocessing
import numpy as np
from sklearn import neighbors
# 对area变量作对数变换
y = np.log1p(forestfires.area)
# 将X变量作标准化处理
predictors = forestfires.columns[:-1]
X = preprocessing.scale(forestfires[predictors])
# 将数据拆分为训练集和测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)
# 构建默认参数的SVM回归模型
svr = svm.SVR()
# 模型在训练数据集上的拟合
svr.fit(X_train,y_train)
# 模型在测试上的预测
pred_svr = svr.predict(X_test)
# 计算模型的MSE
metrics.mean_squared_error(y_test,pred_svr)
# 使用网格搜索法，选择SVM回归中的最佳C值、epsilon值和gamma值
epsilon = np.arange(0.1,1.5,0.2)
C= np.arange(100,1000,200)
gamma = np.arange(0.001,0.01,0.002)
parameters = {'epsilon':epsilon,'C':C,'gamma':gamma}
grid_svr = model_selection.GridSearchCV(estimator = svm.SVR(max_iter=10000),param_grid =parameters,
                                        scoring='neg_mean_squared_error',cv=5,verbose =1, n_jobs=2)
# 模型在训练数据集上的拟合
grid_svr.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
print(grid_svr.best_params_, grid_svr.best_score_)
# 模型在测试集上的预测
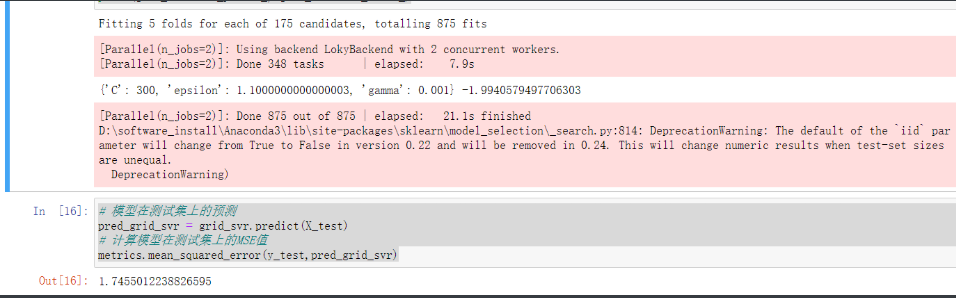
pred_grid_svr = grid_svr.predict(X_test)
# 计算模型在测试集上的MSE值
metrics.mean_squared_error(y_test,pred_grid_svr)

Kmeans聚类(K均值聚类)

'''这个方法就是对SVM模型的优化 可以将特异点单独分离'''
# K值的求解(K代表分几类)
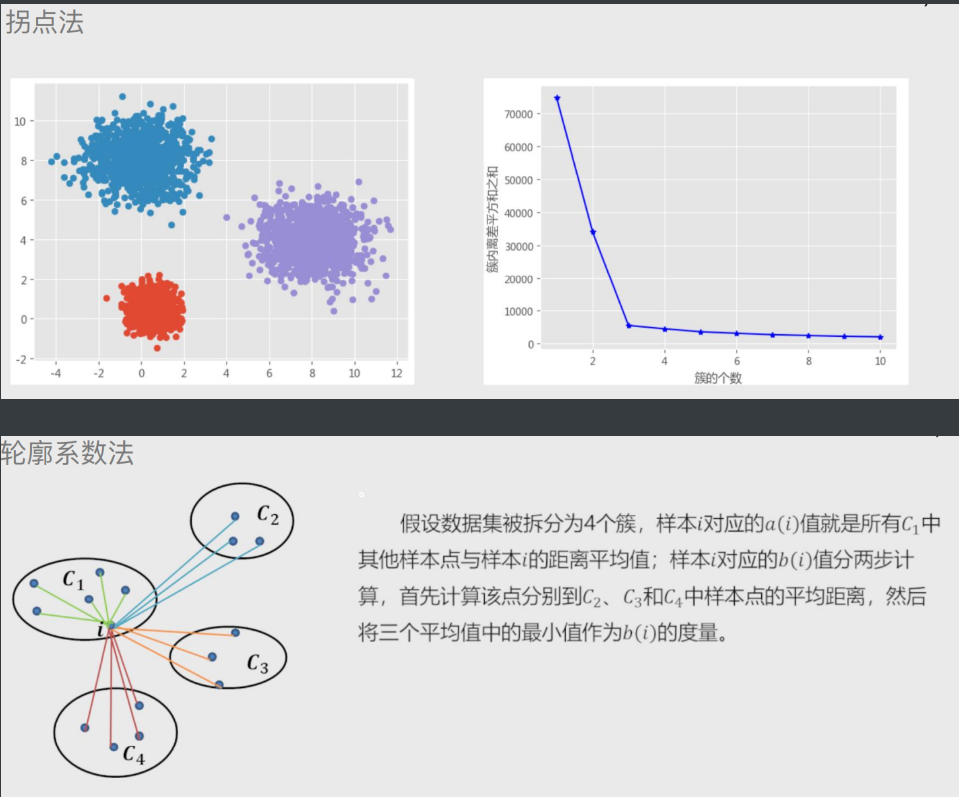
拐点法:
    计算不同类K值下 各簇类种离差平方和(看斜率 变化越明显越好)
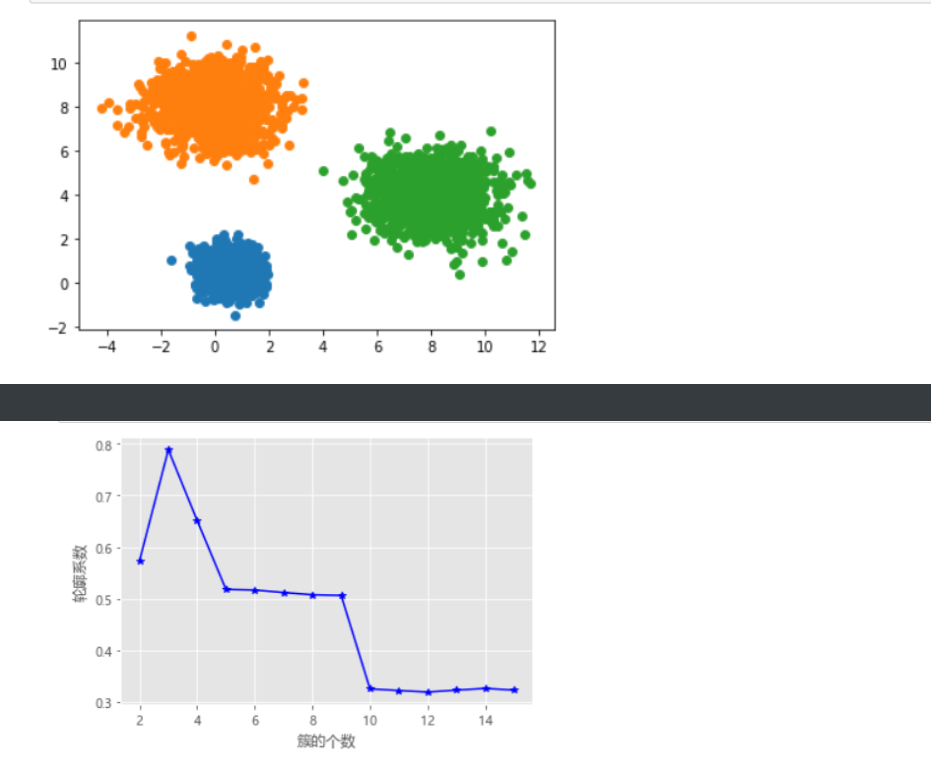
轮廓系数法:
    计算轮廓系数(看大小 越大越好)

Kmeans聚类模型小代码

# 导入第三方包
import pandas as pd
import numpy as np  
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import metrics

# 随机生成三组二元正态分布随机数 
np.random.seed(1234)
mean1 = [0.5, 0.5]
cov1 = [[0.3, 0], [0, 0.3]]
x1, y1 = np.random.multivariate_normal(mean1, cov1, 1000).T

mean2 = [0, 8]
cov2 = [[1.5, 0], [0, 1]]
x2, y2 = np.random.multivariate_normal(mean2, cov2, 1000).T

mean3 = [8, 4]
cov3 = [[1.5, 0], [0, 1]]
x3, y3 = np.random.multivariate_normal(mean3, cov3, 1000).T

# 绘制三组数据的散点图
plt.scatter(x1,y1)
plt.scatter(x2,y2)
plt.scatter(x3,y3)
# 显示图形
plt.show()
# 构造自定义函数，用于绘制不同k值和对应总的簇内离差平方和的折线图
def k_SSE(X, clusters):
    # 选择连续的K种不同的值
    K = range(1,clusters+1)
    # 构建空列表用于存储总的簇内离差平方和
    TSSE = []
    for k in K:
        # 用于存储各个簇内离差平方和
        SSE = []
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        # 返回簇标签
        labels = kmeans.labels_
        # 返回簇中心
        centers = kmeans.cluster_centers_
        # 计算各簇样本的离差平方和，并保存到列表中
        for label in set(labels):
            SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2))
        # 计算总的簇内离差平方和 
        TSSE.append(np.sum(SSE))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')
    # 绘制K的个数与GSSE的关系
    plt.plot(K, TSSE, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('簇内离差平方和之和')
    # 显示图形
    plt.show()

# 将三组数据集汇总到数据框中
X = pd.DataFrame(np.concatenate([np.array([x1,y1]),np.array([x2,y2]),np.array([x3,y3])], axis = 1).T)
# 自定义函数的调用
k_SSE(X, 15)
# 构造自定义函数，用于绘制不同k值和对应轮廓系数的折线图
def k_silhouette(X, clusters):
    K = range(2,clusters+1)
    # 构建空列表，用于存储个中簇数下的轮廓系数
    S = []
    for k in K:
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        labels = kmeans.labels_
        # 调用字模块metrics中的silhouette_score函数，计算轮廓系数
        S.append(metrics.silhouette_score(X, labels, metric='euclidean'))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')    
    # 绘制K的个数与轮廓系数的关系
    plt.plot(K, S, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('轮廓系数')
    # 显示图形
    plt.show()
    
# 自定义函数的调用
k_silhouette(X, 15)

# 读取iris数据集
iris = pd.read_csv(r'iris.csv')
# 查看数据集的前几行
iris.head()
# 提取出用于建模的数据集X
X = iris.drop(labels = 'Species', axis = 1)
# 构建Kmeans模型
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
# 聚类结果标签
X['cluster'] = kmeans.labels_
# 各类频数统计
X.cluster.value_counts()
# 导入第三方模块
import seaborn as sns

# 三个簇的簇中心
centers = kmeans.cluster_centers_
# 绘制聚类效果的散点图
sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'cluster', markers = ['^','s','o'], 
           data = X, fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False)
plt.scatter(centers[:,2], centers[:,3], marker = '*', color = 'black', s = 130)
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
# 图形显示
plt.show()
# 增加一个辅助列，将不同的花种映射到0,1,2三种值，目的方便后面图形的对比
iris['Species_map'] = iris.Species.map({'virginica':0,'setosa':1,'versicolor':2})
# 绘制原始数据三个类别的散点图
sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'Species_map', data = iris, markers = ['^','s','o'],
           fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False)
plt.xlabel('花瓣长度')
plt.ylabel('花瓣宽度')
# 图形显示
plt.show()

# 读取球员数据
players = pd.read_csv(r'players.csv')
players.head()
# 绘制得分与命中率的散点图
sns.lmplot(x = '得分', y = '命中率', data = players, 
           fit_reg = False, scatter_kws = {'alpha':0.8, 'color': 'steelblue'})
plt.show()
from sklearn import preprocessing
# 数据标准化处理
X = preprocessing.minmax_scale(players[['得分','罚球命中率','命中率','三分命中率']])
# 将数组转换为数据框
X = pd.DataFrame(X, columns=['得分','罚球命中率','命中率','三分命中率'])
# 使用拐点法选择最佳的K值
k_SSE(X, 15)
# 使用轮廓系数选择最佳的K值
k_silhouette(X, 10)
# 将球员数据集聚为3类
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
# 将聚类结果标签插入到数据集players中
players['cluster'] = kmeans.labels_
# 构建空列表，用于存储三个簇的簇中心
centers = []
for i in players.cluster.unique():
    centers.append(players.ix[players.cluster == i,['得分','罚球命中率','命中率','三分命中率']].mean())
# 将列表转换为数组，便于后面的索引取数
centers = np.array(centers)

# 绘制散点图
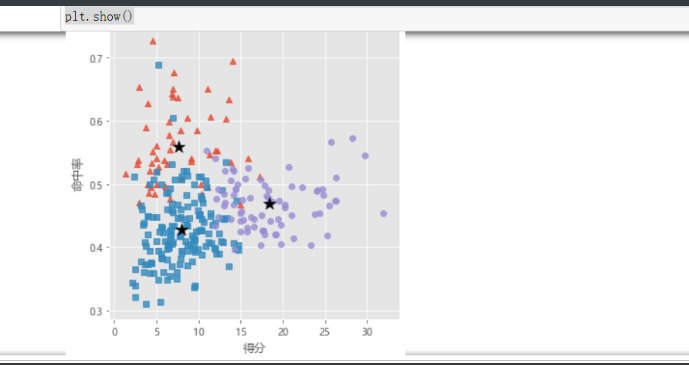
sns.lmplot(x = '得分', y = '命中率', hue = 'cluster', data = players, markers = ['^','s','o'],
           fit_reg = False, scatter_kws = {'alpha':0.8}, legend = False)
# 添加簇中心
plt.scatter(centers[:,0], centers[:,2], c='k', marker = '*', s = 180)
plt.xlabel('得分')
plt.ylabel('命中率')
# 图形显示
plt.show()

DBSCAN聚类(密度聚类)

# K值聚类缺点
1.聚类效果容易受异常样本点影响
2.无法准确将非球形样本进行合理聚类
'''可以采用密度聚类解决上述两个缺点'''

核心对象:内部含有至少大于等于最少样本点的样本
非核心对象:内部少于最少样本点的样本
直接密度可达:在核心对象内部的样本点到核心对象的距离
密度可达:多个直接密度可达链接了多个核心对象(首尾点密度可达)
密度相连:两边的点由中间的核心对象分别密度可达

DBSCAN聚类小实战

# 导入第三方模块
import pandas as pd
import numpy as np
from sklearn.datasets.samples_generator import make_blobs
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import cluster
# 模拟数据集
X,y = make_blobs(n_samples = 2000, centers = [[-1,-2],[1,3]], cluster_std = [0.5,0.5], random_state = 1234)
# 将模拟得到的数组转换为数据框，用于绘图
plot_data = pd.DataFrame(np.column_stack((X,y)), columns = ['x1','x2','y'])
# 设置绘图风格
plt.style.use('ggplot')
# 绘制散点图（用不同的形状代表不同的簇）
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o'],
           fit_reg = False, legend = False)
# 显示图形
plt.show()
# 导入第三方模块
from sklearn import cluster
# 构建Kmeans聚类和密度聚类
kmeans = cluster.KMeans(n_clusters=2, random_state=1234)
kmeans.fit(X)
dbscan = cluster.DBSCAN(eps = 0.5, min_samples = 10)
dbscan.fit(X)
# 将Kmeans聚类和密度聚类的簇标签添加到数据框中
plot_data['kmeans_label'] = kmeans.labels_
plot_data['dbscan_label'] = dbscan.labels_

# 绘制聚类效果图
# 设置大图框的长和高
plt.figure(figsize = (12,6))
# 设置第一个子图的布局
ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0))
# 绘制散点图
ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label)
# 设置第二个子图的布局
ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1))
# 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致，通过序列的map“方法”对颜色作重映射)
ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:2,1:0}))
# 显示图形
plt.show()
# 导入第三方模块
from sklearn.datasets.samples_generator import make_moons
# 构造非球形样本点
X1,y1 = make_moons(n_samples=2000, noise = 0.05, random_state = 1234)
# 构造球形样本点
X2,y2 = make_blobs(n_samples=1000, centers = [[3,3]], cluster_std = 0.5, random_state = 1234)
# 将y2的值替换为2(为了避免与y1的值冲突，因为原始y1和y2中都有0这个值)
y2 = np.where(y2 == 0,2,0)
# 将模拟得到的数组转换为数据框，用于绘图
plot_data = pd.DataFrame(np.row_stack([np.column_stack((X1,y1)),np.column_stack((X2,y2))]), columns = ['x1','x2','y'])

# 绘制散点图（用不同的形状代表不同的簇）
sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o','>'],
           fit_reg = False, legend = False)
# 显示图形
plt.show()
# 构建Kmeans聚类和密度聚类
kmeans = cluster.KMeans(n_clusters=3, random_state=1234)
kmeans.fit(plot_data[['x1','x2']])
dbscan = cluster.DBSCAN(eps = 0.3, min_samples = 5)
dbscan.fit(plot_data[['x1','x2']])
# 将Kmeans聚类和密度聚类的簇标签添加到数据框中
plot_data['kmeans_label'] = kmeans.labels_
plot_data['dbscan_label'] = dbscan.labels_

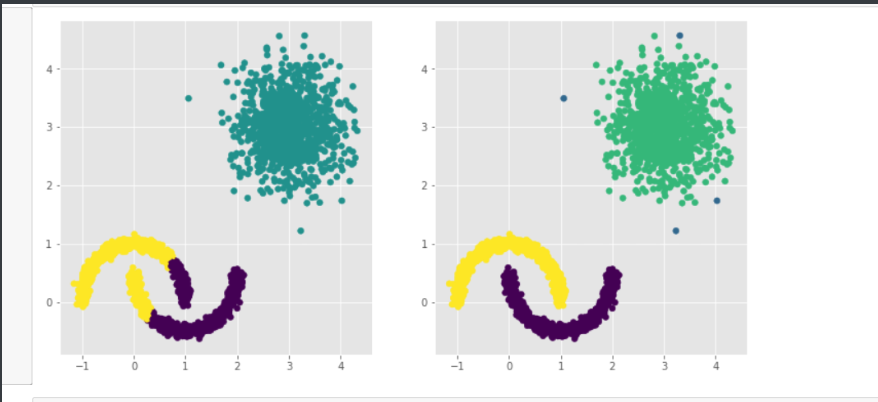
# 绘制聚类效果图
# 设置大图框的长和高
plt.figure(figsize = (12,6))
# 设置第一个子图的布局
ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0))
# 绘制散点图
ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label)
# 设置第二个子图的布局
ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1))
# 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致，通过序列的map“方法”对颜色作重映射)
ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:0,1:3,2:2}))
# 显示图形
plt.show()

# 读取外部数据
Province = pd.read_excel(r'Province.xlsx')
Province.head()
# 绘制出生率与死亡率散点图
plt.scatter(Province.Birth_Rate, Province.Death_Rate, c = 'steelblue')
# 添加轴标签
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')
# 显示图形
plt.show()
# 读入第三方包
from sklearn import preprocessing
# 选取建模的变量
predictors = ['Birth_Rate','Death_Rate']
# 变量的标准化处理
X = preprocessing.scale(Province[predictors])
X = pd.DataFrame(X)
# 构建空列表，用于保存不同参数组合下的结果
res = []
# 迭代不同的eps值
for eps in np.arange(0.001,1,0.05):
    # 迭代不同的min_samples值
    for min_samples in range(2,10):
        dbscan = cluster.DBSCAN(eps = eps, min_samples = min_samples)
        # 模型拟合
        dbscan.fit(X)
        # 统计各参数组合下的聚类个数（-1表示异常点）
        n_clusters = len([i for i in set(dbscan.labels_) if i != -1])
        # 异常点的个数
        outliners = np.sum(np.where(dbscan.labels_ == -1, 1,0))
        # 统计每个簇的样本个数
        stats = str(pd.Series([i for i in dbscan.labels_ if i != -1]).value_counts().values)
        res.append({'eps':eps,'min_samples':min_samples,'n_clusters':n_clusters,'outliners':outliners,'stats':stats})
# 将迭代后的结果存储到数据框中        
df = pd.DataFrame(res)
df
# 根据条件筛选合理的参数组合
df.loc[df.n_clusters == 3, :]
%matplotlib
# 中文乱码和坐标轴负号的处理
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False

# 利用上述的参数组合值，重建密度聚类算法
dbscan = cluster.DBSCAN(eps = 0.801, min_samples = 3)
# 模型拟合
dbscan.fit(X)
Province['dbscan_label'] = dbscan.labels_
# 绘制聚类聚类的效果散点图
sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'dbscan_label', data = Province,
           markers = ['*','d','^','o'], fit_reg = False, legend = False)
# 添加省份标签
for x,y,text in zip(Province.Birth_Rate,Province.Death_Rate, Province.Province):
    plt.text(x+0.1,y-0.1,text, size = 8)
# 添加参考线
plt.hlines(y = 5.8, xmin = Province.Birth_Rate.min(), xmax = Province.Birth_Rate.max(), 
           linestyles = '--', colors = 'red')
plt.vlines(x = 10, ymin = Province.Death_Rate.min(), ymax = Province.Death_Rate.max(), 
           linestyles = '--', colors = 'red')
# 添加轴标签
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')
# 显示图形
plt.show()
# 导入第三方模块
from sklearn import metrics
# 构造自定义函数，用于绘制不同k值和对应轮廓系数的折线图
def k_silhouette(X, clusters):
    K = range(2,clusters+1)
    # 构建空列表，用于存储个中簇数下的轮廓系数
    S = []
    for k in K:
        kmeans = cluster.KMeans(n_clusters=k)
        kmeans.fit(X)
        labels = kmeans.labels_
        # 调用字模块metrics中的silhouette_score函数，计算轮廓系数
        S.append(metrics.silhouette_score(X, labels, metric='euclidean'))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')    
    # 绘制K的个数与轮廓系数的关系
    plt.plot(K, S, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('轮廓系数')
    # 显示图形
    plt.show()
    
# 聚类个数的探索
k_silhouette(X, clusters = 10)
# 利用Kmeans聚类
kmeans = cluster.KMeans(n_clusters = 3)
# 模型拟合
kmeans.fit(X)
Province['kmeans_label'] = kmeans.labels_
# 绘制Kmeans聚类的效果散点图
sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'kmeans_label', data = Province,
           markers = ['d','^','o'], fit_reg = False, legend = False)
# 添加轴标签
plt.xlabel('Birth_Rate')
plt.ylabel('Death_Rate')
plt.show()

GBDT模型

Adaboost算法(既可以解决分类问题也可以解决预测问题)
	由多颗基础决策树组成 并且这些决策树彼此之间有先后关系

SMOTE算法
	通过算法将比例较少的数据样本扩大

电脑的种类

• 台式机

• 笔记本

• 服务器

  作用:
  	1.可以尽量避免数据不会丢失
    	2.可以24小时不间断提供服务
    	3.可以提升用户体验
  ps:运维人员的工作，本质上就是为了上述三点的实现
  

服务器种类

云主机服务器
	将多台硬件服务器进行整合,根据用户的需求分配硬件资源给相应用户
物理主机服务器
	机架式服务器
	刀片服务器
	塔式服务器

服务器的品牌

戴尔dell(常见)
华为
IBM(被联想收购更名为thinkserver)
浪潮(国内居多)
...

"""
服务器尺寸描述主要以U为单位
	1U=1.75英寸=4.445CM=4.45CM
	常见服务器尺寸 1U 2U 4U
"""

服务器内部组成

电源  主板 CPU 内存 硬盘 散热系统
	
工作原理
	1) 电源:
	   冗余技术: 
        	UPS(不间断电源系统)、双路或多路供电、发电机
	   
	2) CPU: 做数据运算处理
	   CPU路数
	   		单路==1个   双路==2个  四路==4个
	   CPU核数
	   		把CPU比喻成厂房, 将CPU中的核数比喻成厂房中的工人, CPU核数是真正处理工作任务,CPU核数越多, 同时处理工作任务的效率越高
	   
	3) 内存: 临时存储数据(断电数据即丢失)
	   程序       进程(存储在内存中)        守护进程
	   代码       运行起来的程序            根本停不下来的进程
	   
	   缓存cache  缓冲buffer
        内存存储空间一分为二(公交车上下车位置)
        	cache缓存   从缓存读数据 
        	buffer缓冲  从缓冲写数据 
		 
     企业案例:
        高并发存储数据环境
      		存: 将数据先存储到内存 在存储到磁盘中
      		读: 将磁盘中的热点数据存储到内存中
        低并发存储数据环境	
      		存: 将数据先放到硬盘里
      		读: 将磁盘中的热点数据存储到内存中
            
	4) 硬盘: 永久存储数据(断电数据不会丢失)
    		硬盘种类：
	   			机械硬盘（性能低） 
        		固态硬盘（性能高）
          硬盘接口（茶壶壶嘴）：SATA< SCSI <SAS <PCI-E
          
	   		服务器磁盘阵列（raid）
           1）服务器上有多块硬盘保证数据不容易丢失
           2）服务器上存储数据较多可以将多块硬盘进行整合
           3）服务器上存储大容量数据效率更高

	   服务器磁盘阵列(raid)  见下图
    		按照不同级别进行多块硬盘整合
       	2块（raid0 raid1） 3块（raid5） 4块（raid01 raid10） 
       	raid0 ：存储量-没有浪费 
       		优势：提升数据存储效率
         	缺点：容易丢失数据

         raid1：存储量-浪费一半
       		优势：不容易丢失数据，数据更加安全
         	缺点：数据存储效率较低

         raid5：（至少需要3块硬盘）存储量--损失一块盘容量	 
         	优势：安全 存储数据性能也比较高	
         	缺点：最多只能坏一块盘
          
	5）远程管理卡
       远程控制管理服务器的运行状态
       远程安装操作系统
       远程配置raid阵列信息	   
	   	 PS：一定要确认远程管理卡的默认地址信息
	
	6）光驱（安装系统）-- 淘汰
       U盘安装系统
       kickstart cobbler -- 无人值守安装系统
	   
	7）机柜
       机柜里面线缆一定要布线整齐 设置标签

虚拟化

存储知识
	什么是虚拟化?
  	将一台计算机硬件"拆分"成多份分配使用
    
如何实现虚拟化
	vmware软件		
  	vmware12  			支持windows64
    vmware8	  			支持windows32
    vmware fusion  	支持苹果系统
	链接: https://pan.baidu.com/s/1K3uuK2D6WIKnblllplPPdQ  
  密码: o1vu

创建虚拟主机
	参考详细图示即可
  	注意事项
    	内存设置
      	内存比较多分配 每个虚拟主机1G（建议）    
        内存少每个虚拟主机512m 安装系统时建议分配内存2G

配置虚拟主机
	参考详细图示即可
# 一言以蔽之 虚拟化就是将电脑中一部分资源分出来变成另一台电脑