10/22

今日考题
1.如何确定变量之间是否存在线性关系

通过公式硬算关系
通过numpy自带方法  numpy.corrcoef(X,Y)
通过pandas自带方法  pandas.DataFrame({'X':X,'Y':Y}).corr()
得出结果的绝对值大于等于0.8表示高度相关
    绝对值大于等于0.5小于等于0.8表示中度相关
    绝对值大于等于0.3小于0.5表示弱相关
    绝对值小于0.3表示几乎不相关

2.一元线性回归与多元线性回归的区别，并写出各自公式

多元线性回归较于一元线性回归 自变量变多了
一元线性回归模型  y = ax + b + 误差项  (a,b为常数)
多元线性回归模型  y = ax + bx1 + cx2 + ... + d

3.什么是因变量 自变量 离散型变量 哑变量，针对哑变量什么时候用原理是什么

应变量即研究的最后结果 也就是数学模型中的y是只能有一个的
自变量则是影响结果的因素 可以有多个 但是多个之间不能有联系  也是数学模型中的x
离散型变量就是那些只能用整数表示的自变量
哑变量则代表那些无法直接用数字表示出来的变量 通常用0,1的矩阵组合去替代

# 哑变量举例
假设有三个哑变量
A	B	C
则他们对应数字则是
1	0	0
0	1	0
0	0	1
通过这样实现字符类变量转换成数字

复习巩固

• 数据清洗小收尾

酒店类型  酒店评分  游玩时间
1.用re模块  (会比较复杂)
2.用内置方法
.str.extract('正则表达式')

• 如何查找变量之间是否存在线性关系

1.直接散点图
plt.scatter()
2.通过公式计算"相关系数"
	三种计算方式  四种情况

• 一元线性回归模型

# 用来解决影响某个事物的变化元素只有一种条件的情况
	y = a + bx + 误差项
"""
y是因变量 a是截距项 b是斜率项 x是自变量 误差项用于描述无法解释的部分
"""
描点划线:尽可能多的让点落在直线上 其他点到直线的距离的平方和一定要最小
 
案例:工作年限与薪资待遇

• 多元线性回归模型

# 主要用来解决影响某个事物变化的因素有多种的情况
	y = a + b1x2 + b2x2 + b3x3 + ... + 误差项
案例:利润与研发成本、管理成本、营销成本、市场的关系

• 实战代码

代码无需掌握保存好
将来用到的时候拷贝修改参数即可

• 重要概念

1.训练集与测试集
	构建模型数据的时候
    训练集用于创建模型(训练)
    测试集用于模型验证(测试)
    训练集占比一定要比测试集占比大很多(一般82开)
 2.哑变量
	数学模型的构建只能是数字类型的数据参与 非数字类型的数据如果要参与构建需要先转换成数字类型(该过程称之为构造哑变量)
    哑变量构造完成后还需要确保多个哑变量之间不存在多种共线性

内容概要

• 模型的假设检验

• 岭回归与Lasson回归

  主要用来解决线性回归的不足之处
  

• Logistic回归模型

• 决策树与随机森林

• K近邻模型

详细讲解

模型的假设检验(F与T)

F检验(主要检验模型是否合理)

通过公式计算出"统计量"之后再用另一个公式算出"理论值"
之后将两者进行比较 如果'统计值'远大于'理论值'则说明验证成立

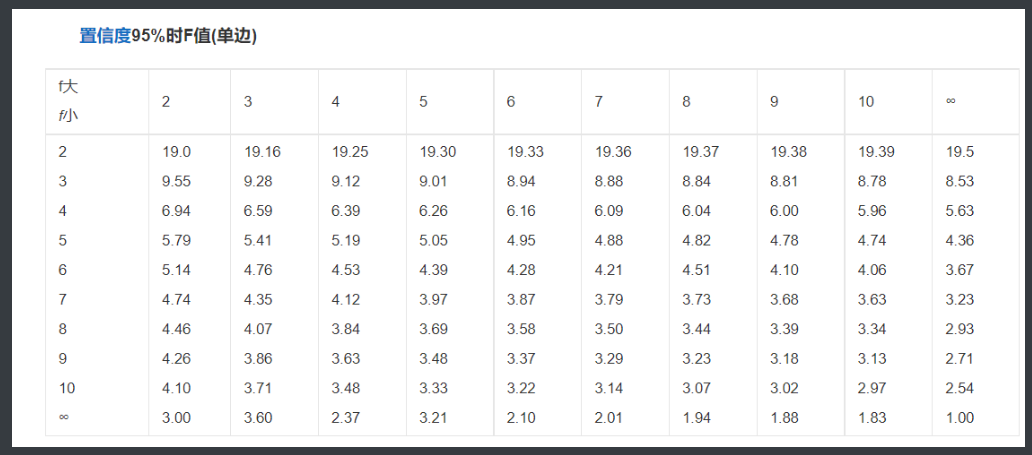
'''接下来看代码'''
# 导⼊第三⽅模块
import numpy as np
# 计算建模数据中因变量的均值
ybar=train.Profit.mean()
# 统计变量个数和观测个数
p=model2.df_model
n=train.shape[0]
# 计算回归离差平⽅和
RSS=np.sum((model2.fittedvalues-ybar)**2)
# 计算误差平⽅和
ESS=np.sum(model2.resid**2)
# 计算F统计量的值
F=(RSS/p)/(ESS/(n-p-1))
print('F统计量的值：',F)
F统计量的值:174.6372
    
# 导⼊模块
from scipy.stats import f
# 计算F分布的理论值
F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1)
print('F分布的理论值为：',F_Theroy)
out:
F分布的理论值为： 2.5026
'''
计算出来的F统计量值174.64远远⼤于F分布的理论值2.50
所以应当拒绝原假设(先假设模型不合理)
原假设就是先假设模型不合理
'''
# 将来只要自己做出模型  然后再把这里代码复制过去用一下就好了

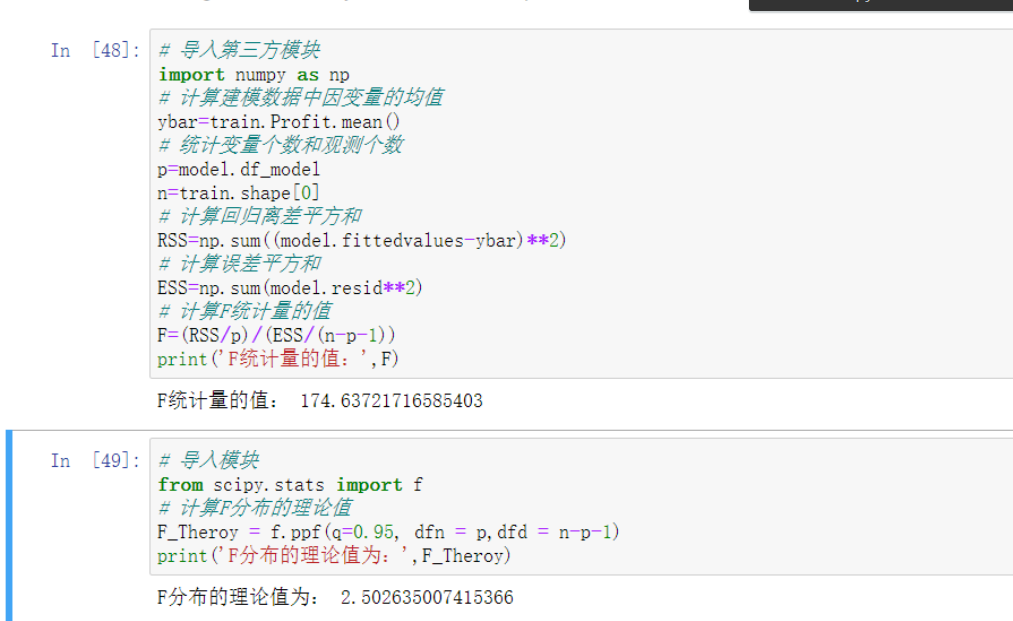
T检验(看参数是否合理)

这个比较简单 直接用之前生成的模型然后调用办法.summary
# 下面生成的这个数据会看起来很专业 其实就.加个方法

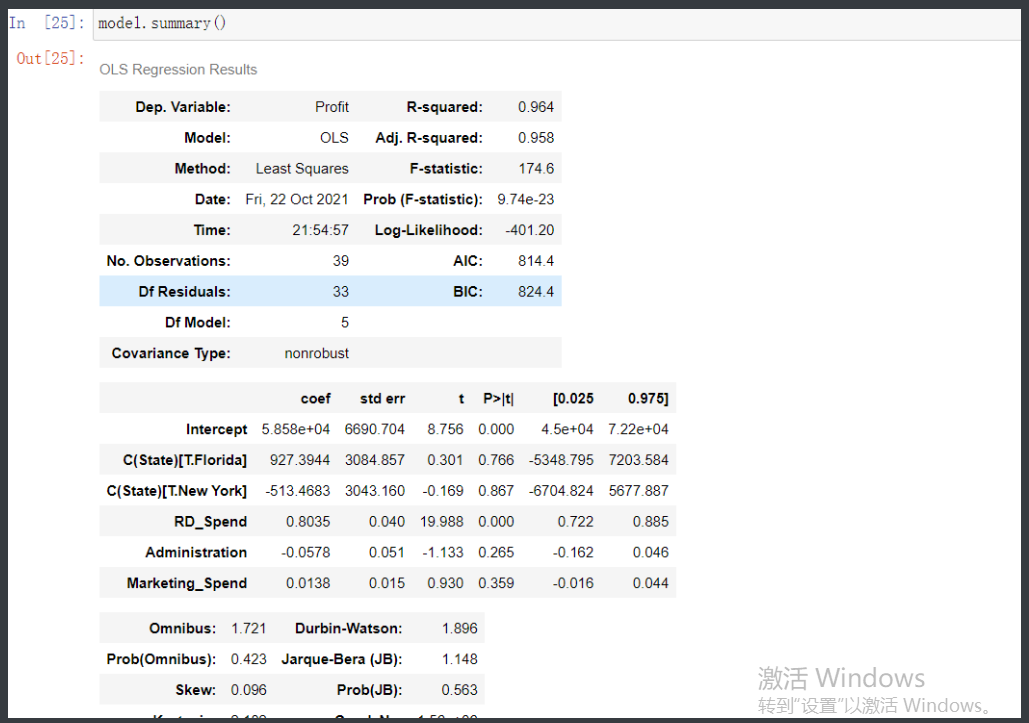
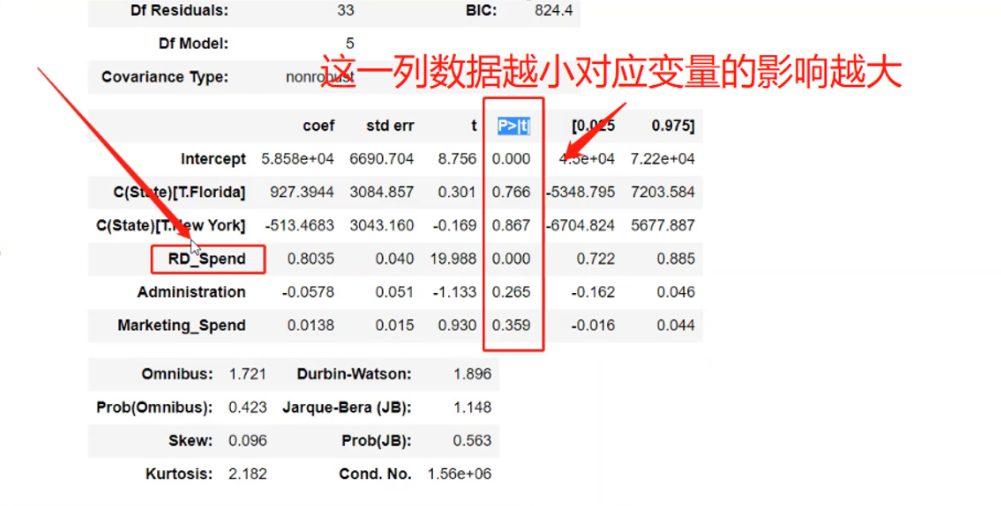
其中最关键的就是P>|T|数据

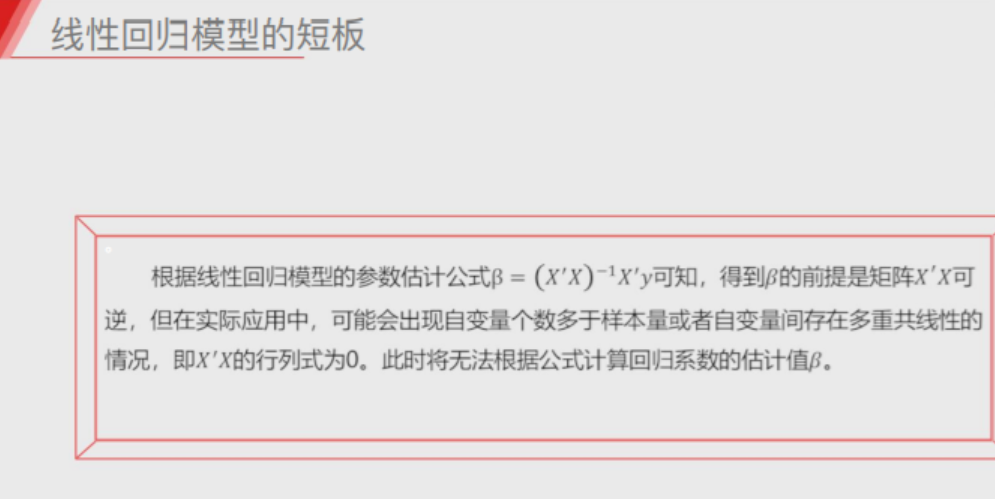
线性回归模型的短板

###########################################################
1.自变量的个数大于样本数量
	比如一家店的购物人数只有3个  但是影响人是否购物的因素有很多大于3
2.自变量之间存在多重共线性
	简单来说就是自变量之间不能有明显的关系 比如昨天配置哑变量中三个州数据
###########################################################

解决线性回归模板短板

岭回归模型

在线性回归模型的基础之上添加一个l2惩罚项(平方项、正则项)
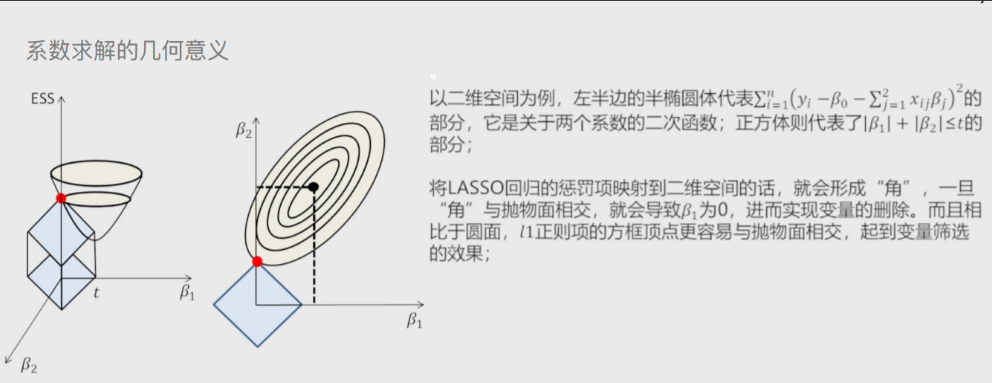
	'''该模型最终转变成求解圆柱体与椭圆抛物线的焦点问题'''

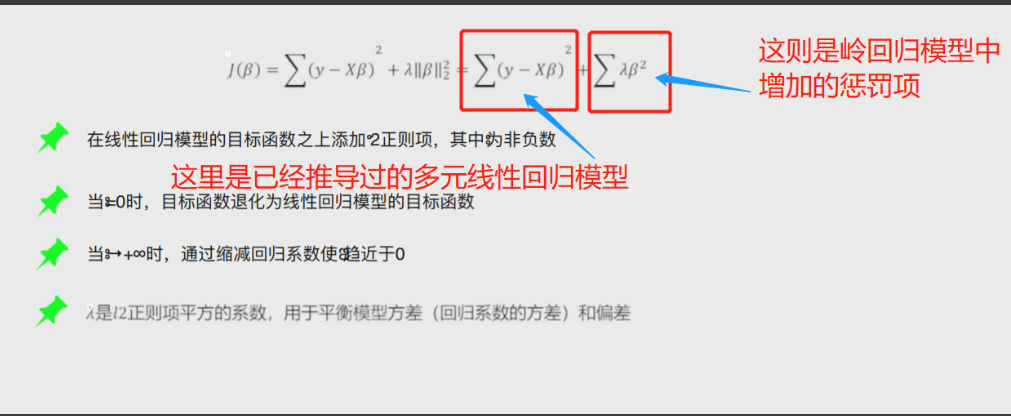
# 凸优化的等价命题
上图中的公式经过凸优化之后就会变成下面途中的公式

这样就将岭回归模型转换成了 求解圆柱体与椭圆抛物线交点的问题

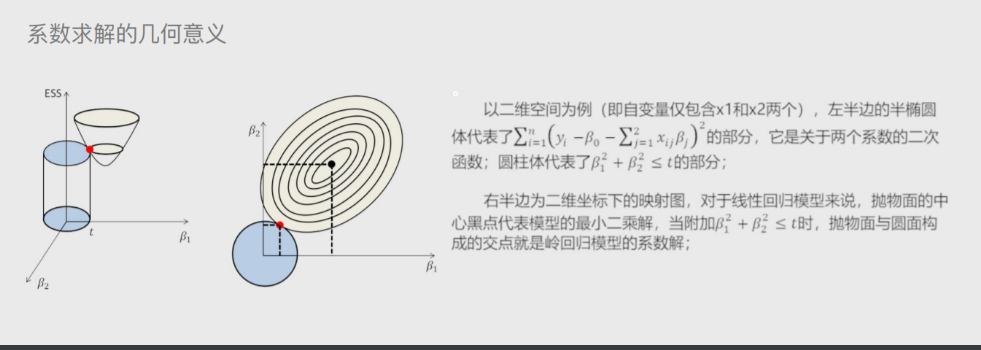
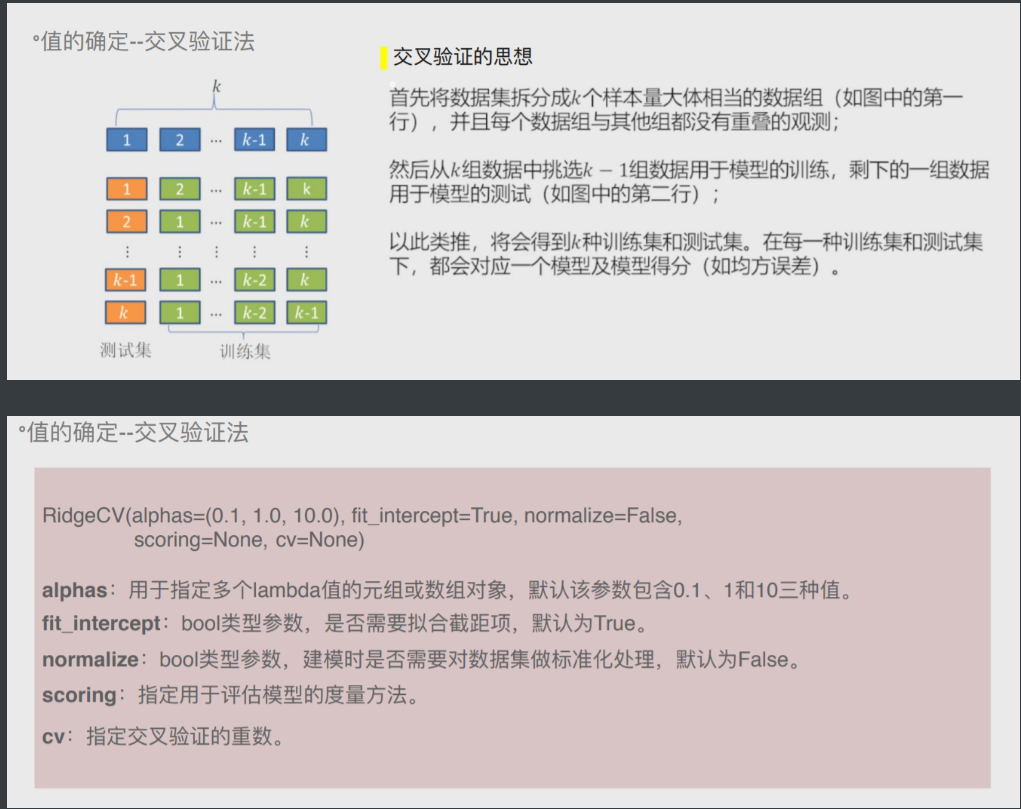
岭回归交叉验证

将所有数据都参与到模型的构建和测试中 最后生成多个模型
再从多个模型中筛选出得分最高(准确度)的模型
'''将所有数据用上多次分类成训练集和测试集
然后多次制作模型 
最后再取出模型中最优的那个'''

岭回归糖尿病小案例

# 导入第三方模块
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import Ridge,RidgeCV
import matplotlib.pyplot as plt

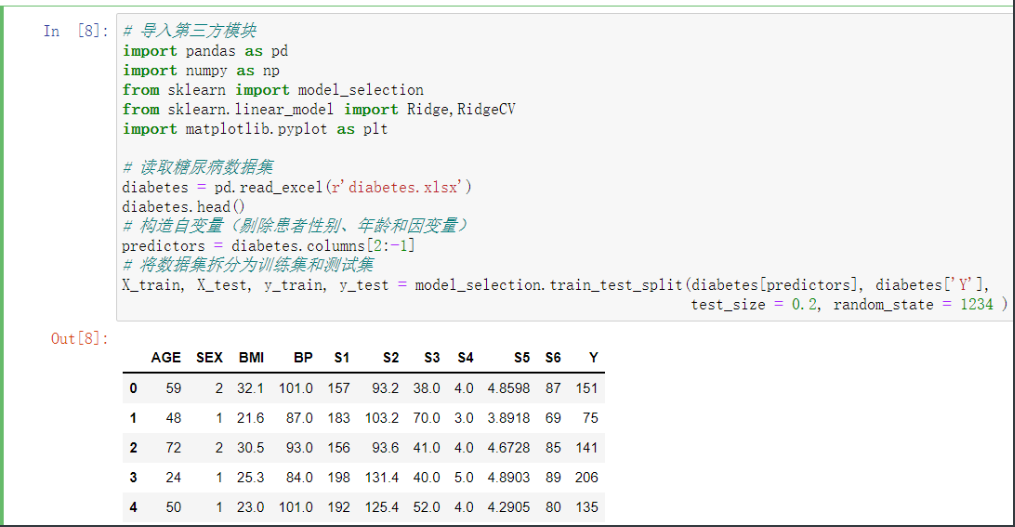
# 读取糖尿病数据集
diabetes = pd.read_excel(r'diabetes.xlsx')
diabetes.head()
# 构造自变量（剔除患者性别、年龄和因变量）
predictors = diabetes.columns[2:-1]
# 将数据集拆分为训练集和测试集
'''在之后稍微有点技术含量的模型都是要拆分4项的'''
X_train, X_test, y_train, y_test = model_selection.train_test_split(diabetes[predictors], diabetes['Y'], 
test_size = 0.2, random_state = 1234 )

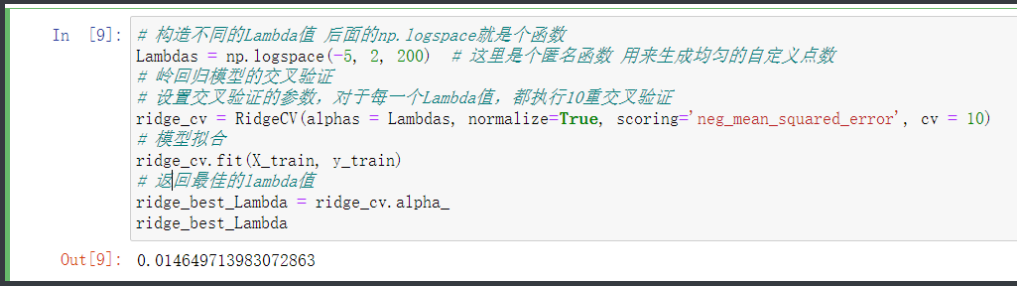
# 构造不同的Lambda值 后面的np.logspace就是个函数
Lambdas = np.logspace(-5, 2, 200)  # 这里是个匿名函数 用来生成均匀的自定义点数
# 岭回归模型的交叉验证
# 设置交叉验证的参数，对于每一个Lambda值，都执行10重交叉验证
ridge_cv = RidgeCV(alphas = Lambdas, normalize=True, scoring='neg_mean_squared_error', cv = 10)
# 模型拟合
ridge_cv.fit(X_train, y_train)
# 返回最佳的lambda值
ridge_best_Lambda = ridge_cv.alpha_
ridge_best_Lambda  # 最后得出Lanbda的值最佳是多少

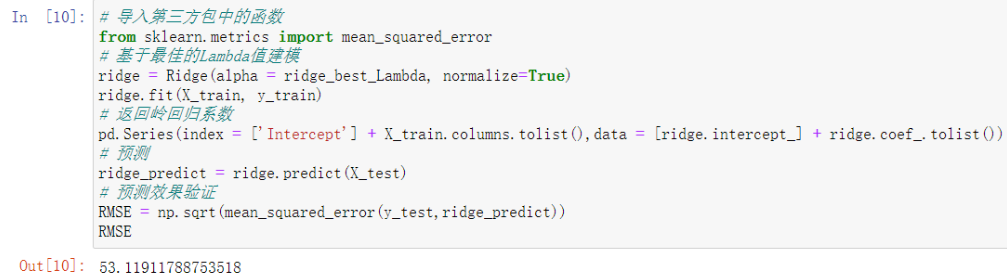
# 导入第三方包中的函数
from sklearn.metrics import mean_squared_error
# 基于最佳的Lambda值建模
ridge = Ridge(alpha = ridge_best_Lambda, normalize=True)
ridge.fit(X_train, y_train)
# 返回岭回归系数
pd.Series(index = ['Intercept'] + X_train.columns.tolist(),data = [ridge.intercept_] + ridge.coef_.tolist())

# 预测
ridge_predict = ridge.predict(X_test)
# 预测效果验证
RMSE = np.sqrt(mean_squared_error(y_test,ridge_predict))
RMSE  # 最后结果53点几已经算是不错了
'''RMSE越小越好'''

Lasso回归模型

在线性回归模型的基础之上添加一个l1惩罚项(绝对值项、正则项)
	相较于岭回归降低了模型的复杂度
    '''该模型最终转变成求解正方体与椭圆抛物线的焦点问题'''

# 同样也进行凸优化
变成下述公式

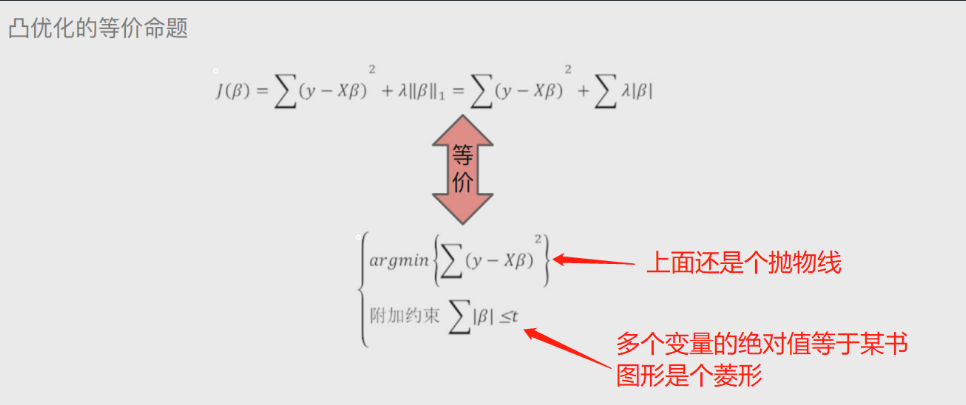
这样Lasso回归模型 就将模型转化成了菱形与抛物线的交点问题
'''角与抛物线的交点'''

Lasso回归交叉验证

和岭回归一样用到交叉验证  两个方法非常相近

Lasso回归糖尿病小案例

# 导入第三方模块中的函数
from sklearn.linear_model import Lasso,LassoCV
# 构造不同的Lambda值 后面的np.logspace就是个函数
Lambdas = np.logspace(-5, 2, 200)  # 这里是个匿名函数 用来生成均匀的自定义点数
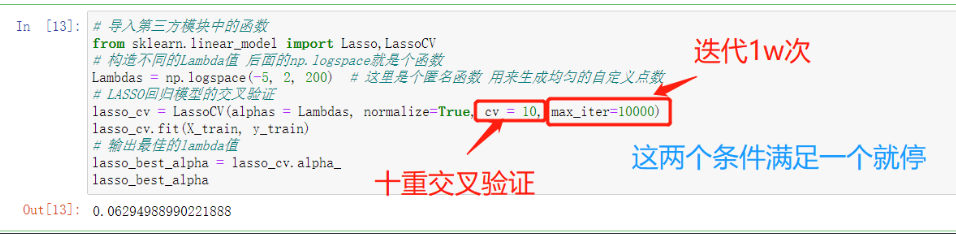
# LASSO回归模型的交叉验证
lasso_cv = LassoCV(alphas = Lambdas, normalize=True, cv = 10, max_iter=10000)
lasso_cv.fit(X_train, y_train)
# 输出最佳的lambda值
lasso_best_alpha = lasso_cv.alpha_
lasso_best_alpha

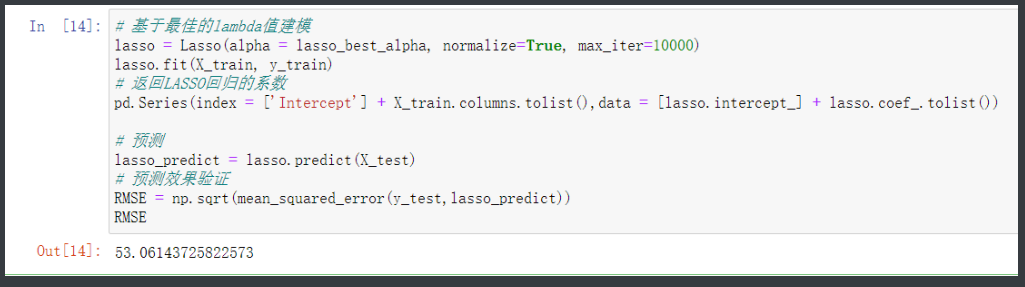
# 基于最佳的lambda值建模
lasso = Lasso(alpha = lasso_best_alpha, normalize=True, max_iter=10000)
lasso.fit(X_train, y_train)
# 返回LASSO回归的系数
pd.Series(index = ['Intercept'] + X_train.columns.tolist(),data = [lasso.intercept_] + lasso.coef_.tolist())

# 预测
lasso_predict = lasso.predict(X_test)
# 预测效果验证
RMSE = np.sqrt(mean_squared_error(y_test,lasso_predict))
RMSE  # 较于岭回归优化了一点

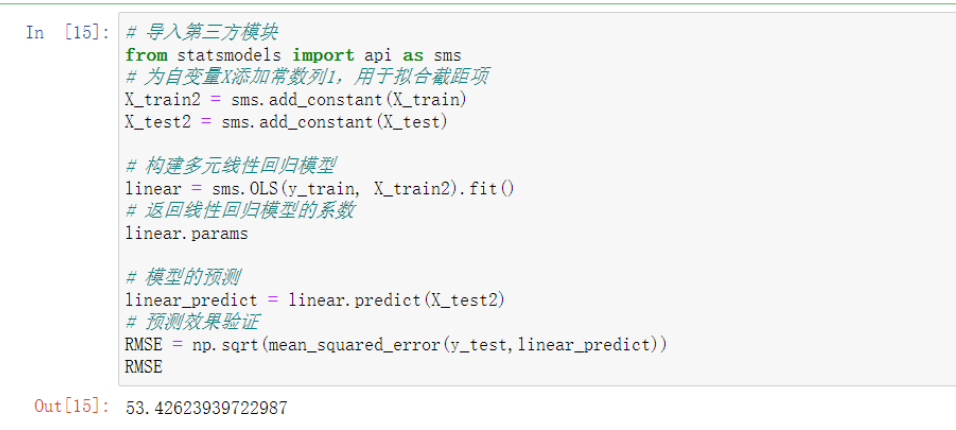
'''最后用线性回归模型作为参考系作为对比'''
# 导入第三方模块
from statsmodels import api as sms
# 为自变量X添加常数列1，用于拟合截距项
X_train2 = sms.add_constant(X_train)
X_test2 = sms.add_constant(X_test)

# 构建多元线性回归模型
linear = sms.OLS(y_train, X_train2).fit()
# 返回线性回归模型的系数
linear.params

# 模型的预测
linear_predict = linear.predict(X_test2)
# 预测效果验证
RMSE = np.sqrt(mean_squared_error(y_test,linear_predict))
RMSE  # 得出的结果雀食略高一点

Logistic回归模型

将线性回归的模型做Logit变换 既为Logistic模型
	将预测问题变成了一个0到1之间的预测值

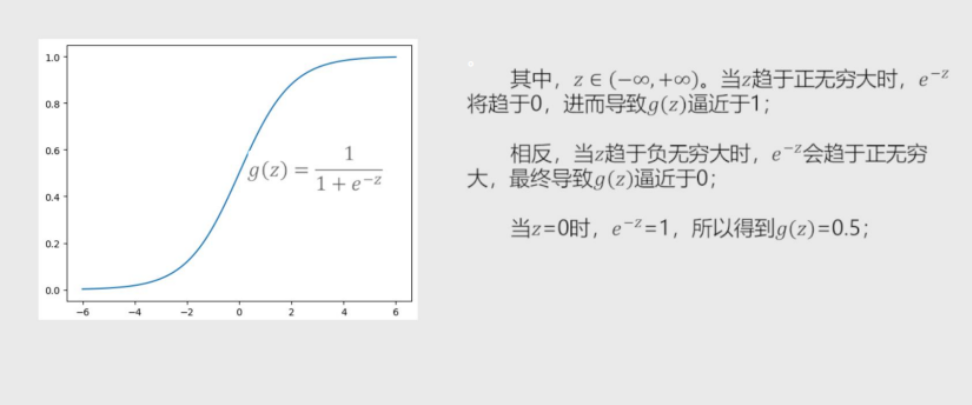
经过一系列优化和求解 最后变成如下数据

以性别和肿瘤作为患癌的参数案例

# 事件发生比 就是上面得到的最后结果

混淆矩阵

混淆矩阵的关键就在下图中的表格和最下面的文字概率
表格部分简单理解就变成了右侧的表

模型的评估方法

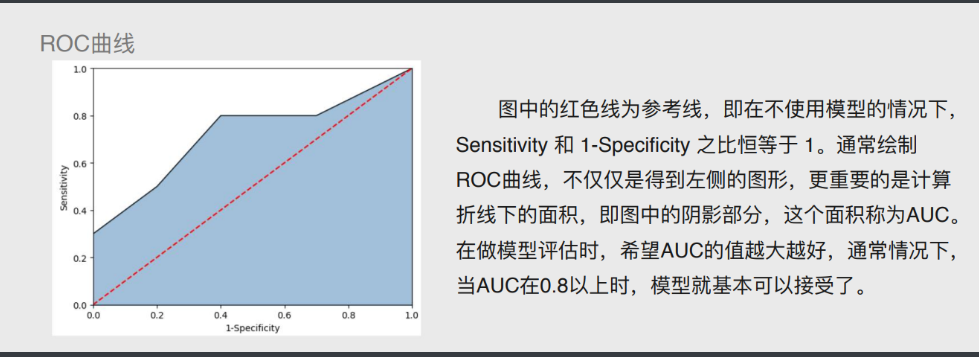
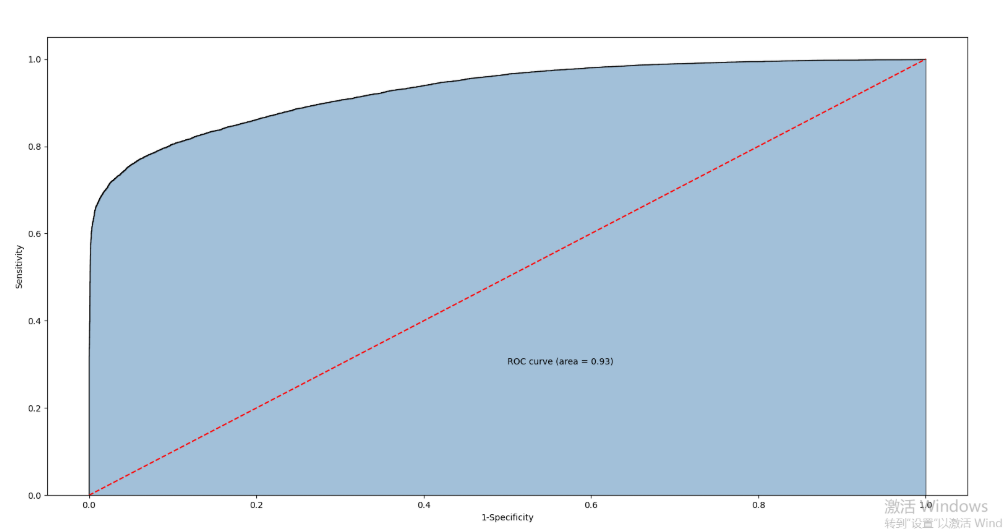
# ROC曲线
	通过计算AUC阴影部分的面积来判断模型是否合理(通常大于0.8表示OK)

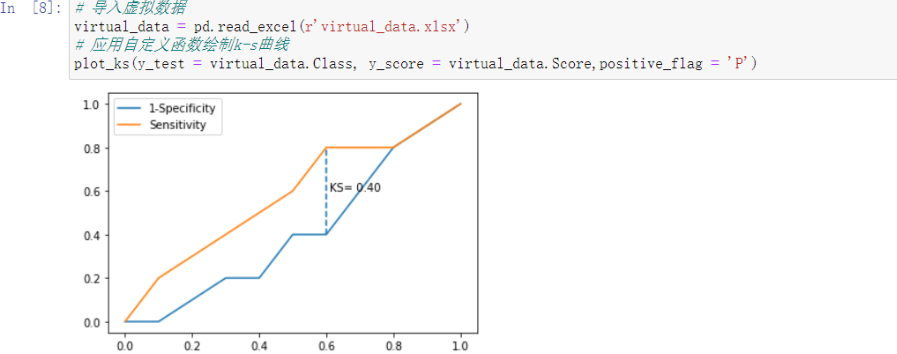
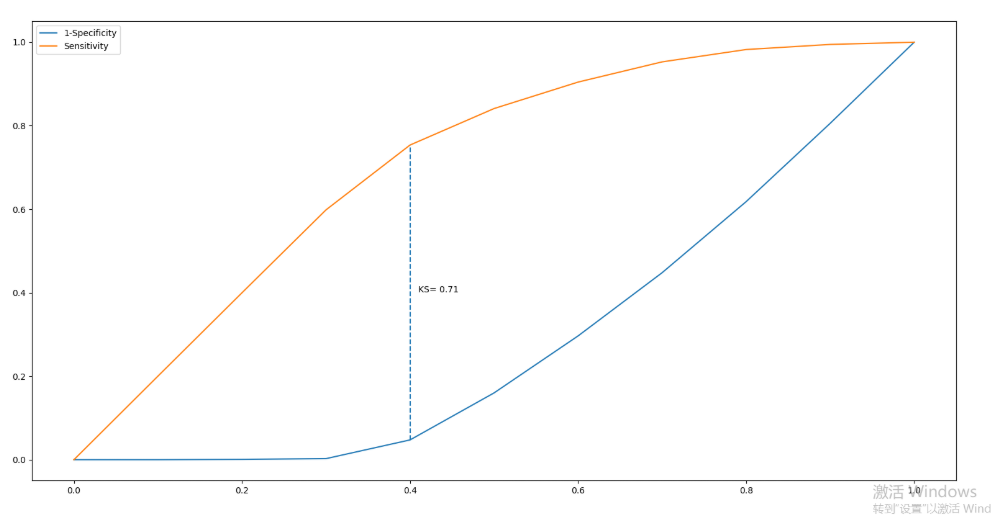
# KS曲线
	通过计算两条折现之间最大距离来衡量模型是否合理(通常大于0.4表示OK)

# 导入第三方模块
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
'''不要慌下面的部分就是一个函数
并不需要掌握
只要到时候需要的时候直接复制过去调用就行了'''
# 自定义绘制ks曲线的函数
def plot_ks(y_test, y_score, positive_flag):
    # 对y_test重新设置索引
    y_test.index = np.arange(len(y_test))
    # 构建目标数据集
    target_data = pd.DataFrame({'y_test':y_test, 'y_score':y_score})
    # 按y_score降序排列
    target_data.sort_values(by = 'y_score', ascending = False, inplace = True)
    # 自定义分位点
    cuts = np.arange(0.1,1,0.1)
    # 计算各分位点对应的Score值
    index = len(target_data.y_score)*cuts
    scores = np.array(target_data.y_score)[index.astype('int')]
    # 根据不同的Score值，计算Sensitivity和Specificity
    Sensitivity = []
    Specificity = []
    for score in scores:
        # 正例覆盖样本数量与实际正例样本量
        positive_recall = target_data.loc[(target_data.y_test == positive_flag) & (target_data.y_score>score),:].shape[0]
        positive = sum(target_data.y_test == positive_flag)
        # 负例覆盖样本数量与实际负例样本量
        negative_recall = target_data.loc[(target_data.y_test != positive_flag) & (target_data.y_score<=score),:].shape[0]
        negative = sum(target_data.y_test != positive_flag)
        Sensitivity.append(positive_recall/positive)
        Specificity.append(negative_recall/negative)
    # 构建绘图数据
    plot_data = pd.DataFrame({'cuts':cuts,'y1':1-np.array(Specificity),'y2':np.array(Sensitivity), 
                              'ks':np.array(Sensitivity)-(1-np.array(Specificity))})
    # 寻找Sensitivity和1-Specificity之差的最大值索引
    max_ks_index = np.argmax(plot_data.ks)
    plt.plot([0]+cuts.tolist()+[1], [0]+plot_data.y1.tolist()+[1], label = '1-Specificity')
    plt.plot([0]+cuts.tolist()+[1], [0]+plot_data.y2.tolist()+[1], label = 'Sensitivity')
    # 添加参考线
    plt.vlines(plot_data.cuts[max_ks_index], ymin = plot_data.y1[max_ks_index], 
               ymax = plot_data.y2[max_ks_index], linestyles = '--')
    # 添加文本信息
    plt.text(x = plot_data.cuts[max_ks_index]+0.01,
             y = plot_data.y1[max_ks_index]+plot_data.ks[max_ks_index]/2,
             s = 'KS= %.2f' %plot_data.ks[max_ks_index])
    # 显示图例
    plt.legend()
    # 显示图形
    plt.show()

# 导入虚拟数据
virtual_data = pd.read_excel(r'virtual_data.xlsx')
# 应用自定义函数绘制k-s曲线
plot_ks(y_test = virtual_data.Class, y_score = virtual_data.Score,positive_flag = 'P')

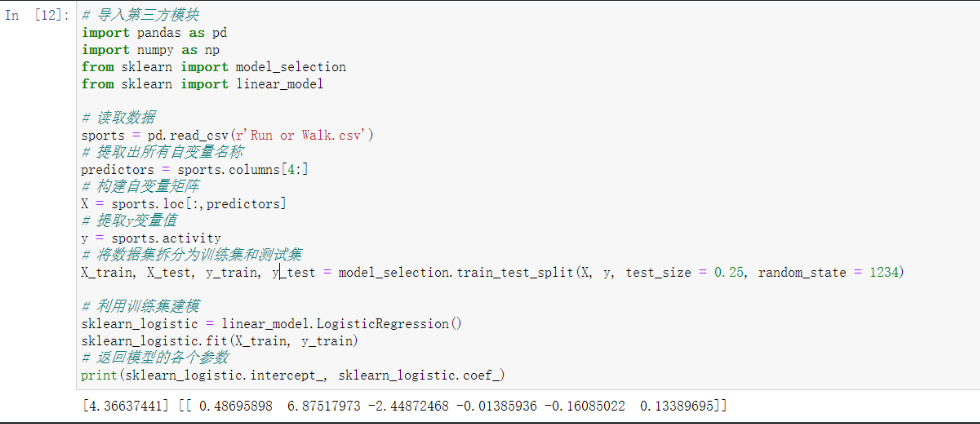
# 导入第三方模块
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn import linear_model

# 读取数据
sports = pd.read_csv(r'Run or Walk.csv')
# 提取出所有自变量名称
predictors = sports.columns[4:]
# 构建自变量矩阵
X = sports.loc[:,predictors]
# 提取y变量值
y = sports.activity
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)

# 利用训练集建模
sklearn_logistic = linear_model.LogisticRegression()
sklearn_logistic.fit(X_train, y_train)
# 返回模型的各个参数
print(sklearn_logistic.intercept_, sklearn_logistic.coef_)

# 模型预测
sklearn_predict = sklearn_logistic.predict(X_test)
# 预测结果统计
pd.Series(sklearn_predict).value_counts()
# 导入第三方模块
from sklearn import metrics
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sklearn_predict, labels = [0,1])
cm

Accuracy = metrics.scorer.accuracy_score(y_test, sklearn_predict)
Sensitivity = metrics.scorer.recall_score(y_test, sklearn_predict)
Specificity = metrics.scorer.recall_score(y_test, sklearn_predict, pos_label=0)
print('模型准确率为%.2f%%:' %(Accuracy*100))
print('正例覆盖率为%.2f%%' %(Sensitivity*100))
print('负例覆盖率为%.2f%%' %(Specificity*100))

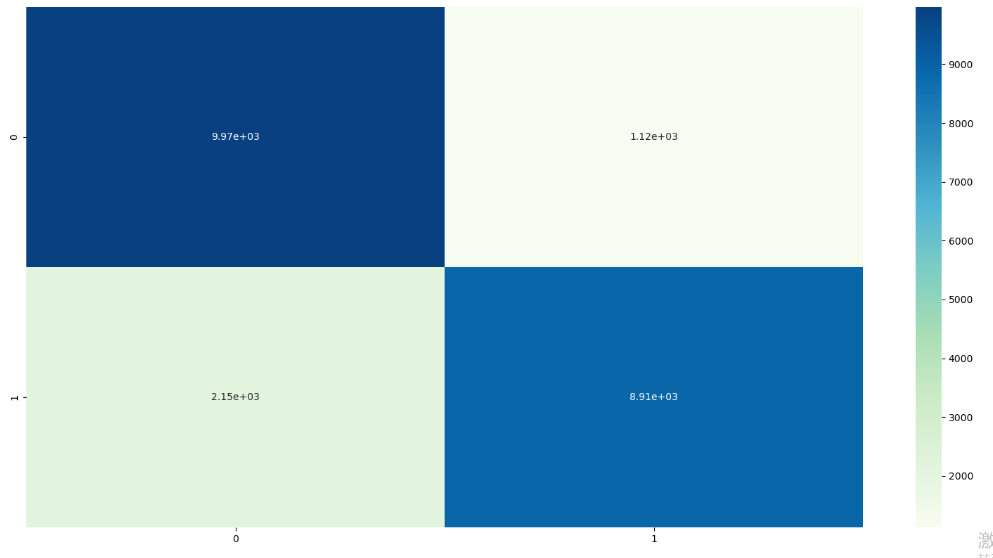
# 混淆矩阵的可视化
# 导入第三方模块
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib
# 绘制热力图
sns.heatmap(cm, annot = True, fmt = '.2e',cmap = 'GnBu')
# 图形显示
plt.show()

sklearn_logistic.predict_proba(X_test)

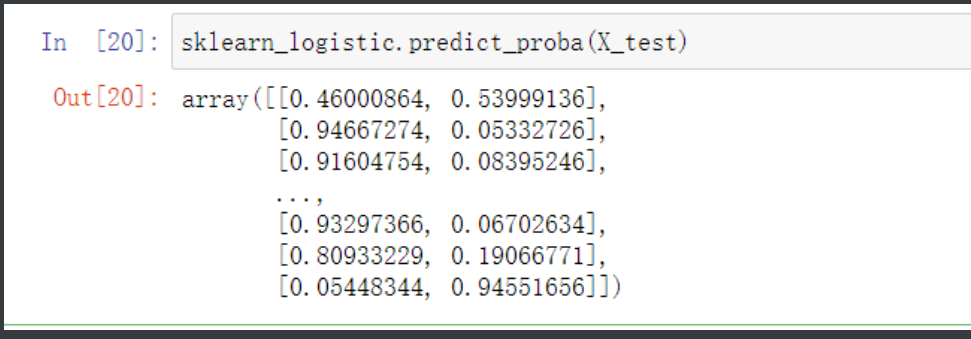
# y得分为模型预测正例的概率
y_score = sklearn_logistic.predict_proba(X_test)[:,1]
# 计算不同阈值下，fpr和tpr的组合值，其中fpr表示1-Specificity，tpr表示Sensitivity
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)

# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

# 调用自定义函数，绘制K-S曲线
plot_ks(y_test = y_test, y_score = y_score, positive_flag = 1)

# -----------------------第一步 建模 ----------------------- #
# 导入第三方模块
import statsmodels.api as sm
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)
# 为训练集和测试集的X矩阵添加常数列1
X_train2 = sm.add_constant(X_train)
X_test2 = sm.add_constant(X_test)
# 拟合Logistic模型
sm_logistic = sm.Logit(y_train, X_train2).fit()
# 返回模型的参数
sm_logistic.params

# -----------------------第二步 预测构建混淆矩阵 ----------------------- #
# 模型在测试集上的预测
sm_y_probability = sm_logistic.predict(X_test2)
# 根据概率值，将观测进行分类，以0.5作为阈值
sm_pred_y = np.where(sm_y_probability >= 0.5, 1, 0)
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sm_pred_y, labels = [0,1])
cm

# -----------------------第三步 绘制ROC曲线 ----------------------- #
# 计算真正率和假正率 
fpr,tpr,threshold = metrics.roc_curve(y_test, sm_y_probability)
# 计算auc的值  
roc_auc = metrics.auc(fpr,tpr)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

# -----------------------第四步 绘制K-S曲线 ----------------------- #
# 调用自定义函数，绘制K-S曲线
sm_y_probability.index = np.arange(len(sm_y_probability))
plot_ks(y_test = y_test, y_score = sm_y_probability, positive_flag = 1)
'''代码的整体思路就是这样做下来'''

决策树

树的概念在SQL中也有提到过
树其实是计算机底层的数据结构
重要概念:
    根节点  起始的最基本的判断要素 所有分支的基础
    枝节点(中间节点)  根节点和枝节点存储的都是条件判断
    叶节点  就是没法再继续分支了

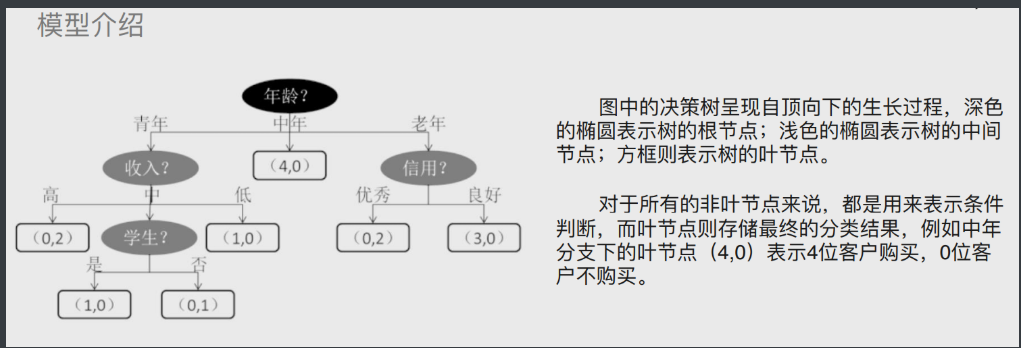
# 信息熵
	eg:  
        信息熵小相当于红路灯  只有三个数据非常有序
        信息熵大相当于买彩票  数据量巨大也就异常混乱

'''信息熵既可以用来解决分类问题(买与不买、带与不带、走与不走)
也可以用来解决预测问题'''
而之前用来解决的则是一些预测问题(具体数值多少)
下图为信息熵案例

条件熵
	其实就是由信息熵再次细分而来
    比如刚才购物的案例中 购买的人我们人为的给他加入一个条件 比如性别

信息增益
	信息增益可以反映出某个条件是否对最终的分类有决定性的影响
	在构建决策树时根节点与枝节点所放的条件按照信息增益由大到小排
'''也就是某个条件对于结果影响的大小
影响越大的条件在构建决策树的时候越要靠根节点放'''

信息增益率
	信息增益会偏向于取值较多的指标  
    为平衡这一现象给他加入了惩罚项 
    即取值越多公式中会除以一个越大的数

基尼指数
	就是通过公式将模型数学化 从而解决连续性变量
    从而实现解决预测性问题  # 最终划归成数学问题

基尼指数增益
	与信息增益类似，还需要考虑⾃变量对因变量的影响程度，即因变量的基尼指数下降速度的快慢，下降得越快，⾃变量对因变量的影响就越强
    基尼指数的惩罚项方式就是去减掉一个出现频率的数

# 函数说明
DecisionTreeClassifier(criterion='gini', splitter='best',
max_depth=None,min_samples_split=2,
min_samples_leaf=1,max_leaf_nodes=None,
class_weight=None)

criterion：⽤于指定选择节点字段的评价指标，对于分类决策树，默认为'gini'，表示采⽤基尼指数选
择节点的最佳分割字段；对于回归决策树，默认为'mse'，表示使⽤均⽅误差选择节点的最佳分割字段
splitter：⽤于指定节点中的分割点选择⽅法，默认为'best'，表示从所有的分割点中选择最佳分割点；
如果指定为'random'，则表示随机选择分割点
max_depth：⽤于指定决策树的最⼤深度，默认为None，表示树的⽣⻓过程中对深度不做任何限制
min_samples_split：⽤于指定根节点或中间节点能够继续分割的最⼩样本量， 默认为2
min_samples_leaf：⽤于指定叶节点的最⼩样本量，默认为1
max_leaf_nodes：⽤于指定最⼤的叶节点个数，默认为None，表示对叶节点个数不做任何限制
class_weight：⽤于指定因变量中类别之间的权重，默认为None，表示每个类别的权重都相等；如果
为balanced，则表示类别权重与原始样本中类别的⽐例成反⽐；还可以通过字典传递类别之间的权重
差异，其形式为{class_label:weight}

随机森林

随机森林中每颗决策树都不限制节点字段选择  # 就是条件节点随便选 尽可能的细分
由这些树组成的随机森林
然后在解决分类问题的时候采用投票法  # 选出要用哪个树
解决预测问题的时候采用均值法  #就是回归模型里那个

泰坦尼克什么人能活小案例

# 导入第三方模块
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn import linear_model
# 读⼊数据
Titanic = pd.read_csv(r'Titanic.csv')
Titanic
# 删除⽆意义的变量，并检查剩余变量是否含有缺失值
Titanic.drop(['PassengerId','Name','Ticket','Cabin'], axis = 1, inplace = True)
Titanic.isnull().sum(axis = 0)
# 对Sex分组，⽤各组乘客的平均年龄填充各组中的缺失年龄
fillna_Titanic = []
for i in Titanic.Sex.unique():
    update = Titanic.loc[Titanic.Sex == i,].fillna(value = {'Age': Titanic.Age[Titanic.Sex == i].mean()}, inplace
    = False)
fillna_Titanic.append(update)
Titanic = pd.concat(fillna_Titanic)
# 使⽤Embarked变量的众数填充缺失值
Titanic.fillna(value = {'Embarked':Titanic.Embarked.mode()[0]}, inplace=True)



# 将数值型的Pclass转换为类别型，否则⽆法对其哑变量处理
Titanic.Pclass = Titanic.Pclass.astype('category')
# 哑变量处理
dummy = pd.get_dummies(Titanic[['Sex','Embarked','Pclass']])
# ⽔平合并Titanic数据集和哑变量的数据集
Titanic = pd.concat([Titanic,dummy], axis = 1)
# 删除原始的Sex、Embarked和Pclass变量
Titanic.drop(['Sex','Embarked','Pclass'], inplace=True, axis = 1)
# 取出所有⾃变量名称
predictors = Titanic.columns[1:]
# 将数据集拆分为训练集和测试集，且测试集的⽐例为25%
X_train, X_test, y_train, y_test = model_selection.train_test_split(Titanic[predictors], Titanic.Survived,
test_size = 0.25, random_state = 1234)


from sklearn.model_selection import GridSearchCV
from sklearn import tree,metrics
# 预设各参数的不同选项值
max_depth = [2,3,4,5,6]
min_samples_split = [2,4,6,8]
min_samples_leaf = [2,4,8,10,12]
# 将各参数值以字典形式组织起来
parameters = {'max_depth':max_depth, 'min_samples_split':min_samples_split,
'min_samples_leaf':min_samples_leaf}
# ⽹格搜索法，测试不同的参数值
grid_dtcateg = GridSearchCV(estimator = tree.DecisionTreeClassifier(), param_grid = parameters, cv=10)
# 模型拟合
grid_dtcateg.fit(X_train, y_train)
# 返回最佳组合的参数值
grid_dtcateg.param_grid


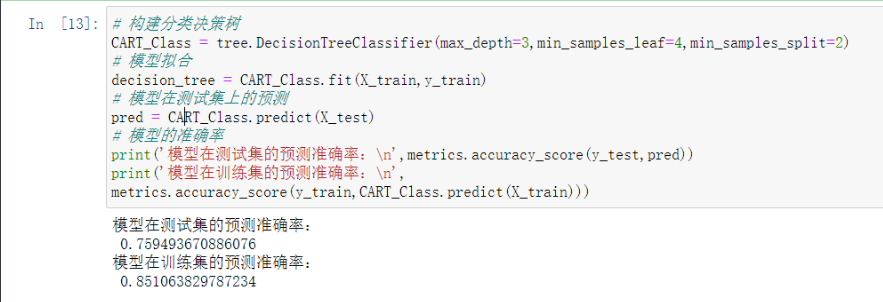
# 构建分类决策树
CART_Class = tree.DecisionTreeClassifier(max_depth=3,min_samples_leaf=4,min_samples_split=2)
# 模型拟合
decision_tree = CART_Class.fit(X_train,y_train)
# 模型在测试集上的预测
pred = CART_Class.predict(X_test)
# 模型的准确率
print('模型在测试集的预测准确率：\n',metrics.accuracy_score(y_test,pred))
print('模型在训练集的预测准确率：\n',
metrics.accuracy_score(y_train,CART_Class.predict(X_train)))

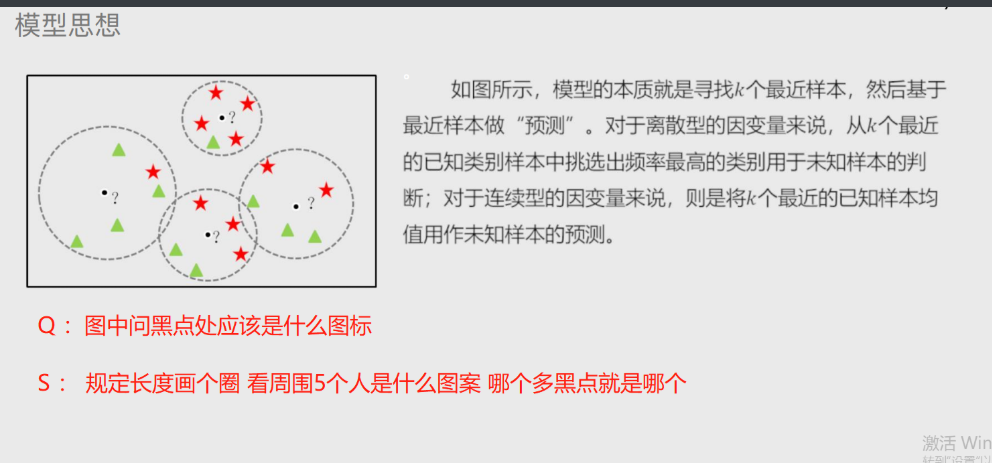
K近邻模型

既可以解决分类问题 也可以解决预测问题
模型思想非常简单请看下图
简单来说就是根据位置样本周边K个邻居样本做出预测
'''重点是K取多少'''

过拟合与欠拟合
	过拟合 就是太过于精确了
    欠拟合 则是太过于模糊
    # 就是精确度一个太高一个太低 太高模型的泛用性就会很差

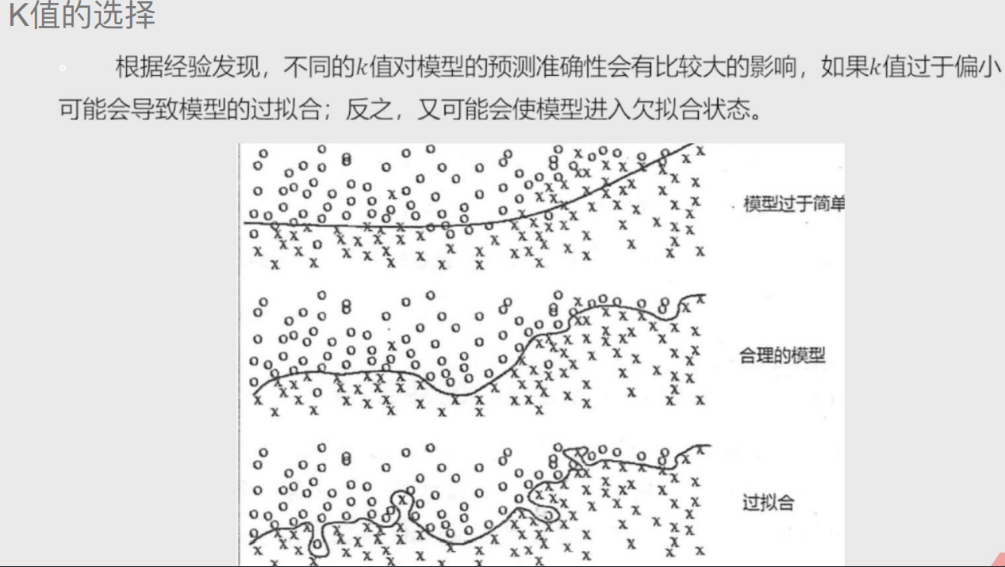
K值选择
	以之前图片中 黑点是什么为例
	距离黑点越近 那个结果的影响就越大
    可以通过更大的权重系数表达
'''准确率越大越好
MSE越小越好'''

# 距离
欧氏距离
就是两点之间的直线距离

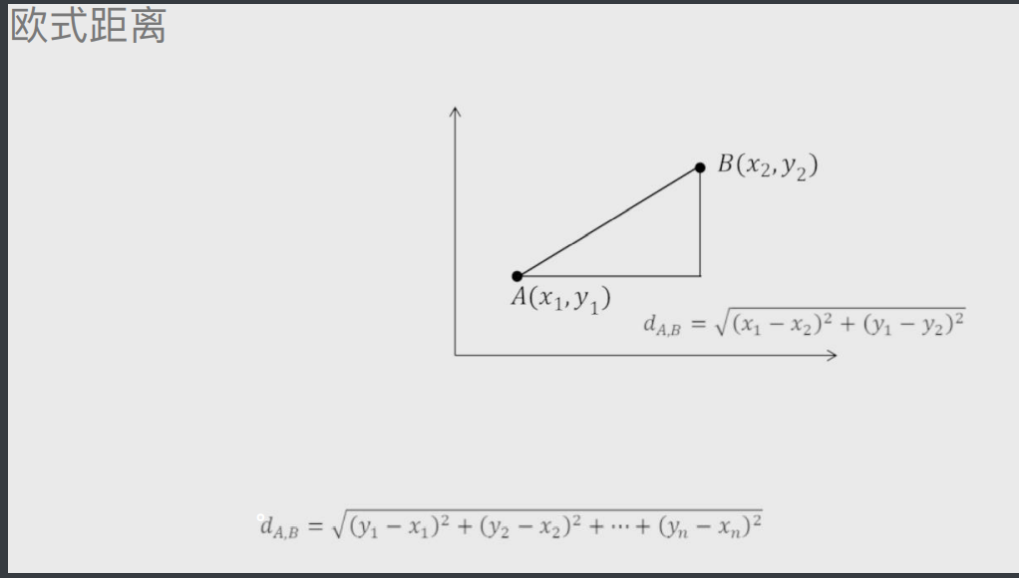
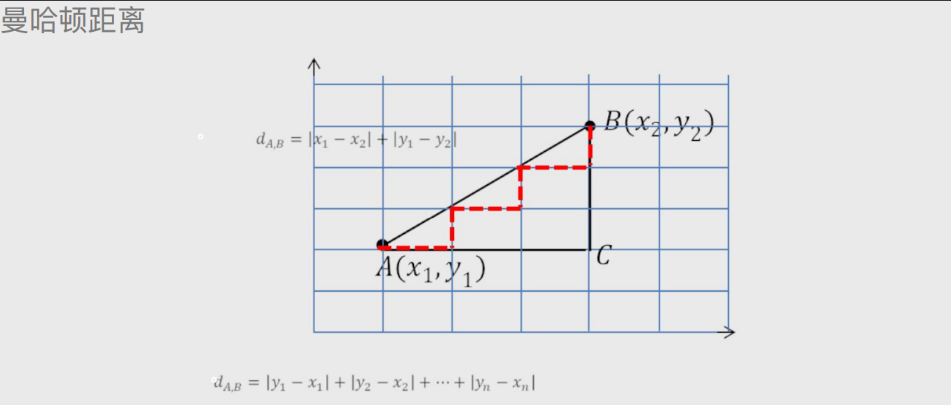
曼哈顿距离  # 曼哈顿街道方方正正的
默认两点之间有障碍物不能直线前进
相当于是将直线距离看成直角三角形的斜边
直角两边相加就是曼哈顿距离

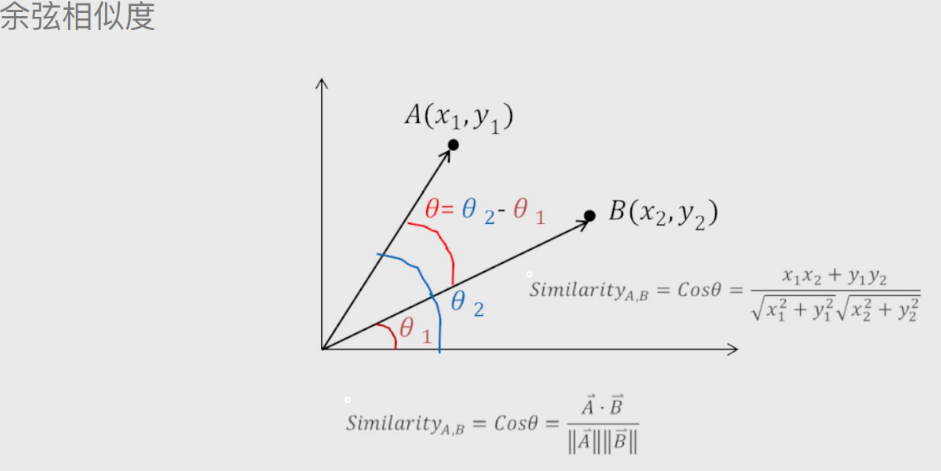
余弦相似度
论文查重就用的余弦相似度

# 代码部分
neighbors.KNeighborsClassifier(n_neighbors=5, weights='uniform',
p=2, metric='minkowski',)

n_neighbors：⽤于指定近邻样本个数K，默认为5
weights：⽤于指定近邻样本的投票权重，默认为'uniform'，表示所有近邻样本的投票权重⼀样；如果
为'distance'，则表示投票权重与距离成反⽐，即近邻样本与未知类别的样本点距离越远，权重越⼩，
反之，权重越⼤
metric：⽤于指定距离的度量指标，默认为闵可夫斯基距离
p：当参数metric为闵可夫斯基距离时，p=1，表示计算点之间的曼哈顿距离；p=2，表示计算点之间
的欧⽒距离；该参数的默认值为2

Knowlege小案例

# 导入第三方包
import pandas as pd
# 导入数据
Knowledge = pd.read_excel(r'Knowledge.xlsx')
# 返回前5行数据
Knowledge.head()
# 构造训练集和测试集
# 导入第三方模块
from sklearn import model_selection
# 将数据集拆分为训练集和测试集
predictors = Knowledge.columns[:-1]
predictors
X_train, X_test, y_train, y_test = model_selection.train_test_split(Knowledge[predictors], Knowledge.UNS, 
                                                                    test_size = 0.25, random_state = 1234)
# 导入第三方模块
import numpy as np
from sklearn import neighbors
import matplotlib.pyplot as plt

# 设置待测试的不同k值
K = np.arange(1,np.ceil(np.log2(Knowledge.shape[0]))).astype(int)
# 构建空的列表，用于存储平均准确率
accuracy = []
for k in K:
    # 使用10重交叉验证的方法，比对每一个k值下KNN模型的预测准确率
    cv_result = model_selection.cross_val_score(neighbors.KNeighborsClassifier(n_neighbors = k, weights = 'distance'), 
                                                X_train, y_train, cv = 10, scoring='accuracy')
    accuracy.append(cv_result.mean())

# 从k个平均准确率中挑选出最大值所对应的下标    
arg_max = np.array(accuracy).argmax()
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
# 绘制不同K值与平均预测准确率之间的折线图
plt.plot(K, accuracy)
# 添加点图
plt.scatter(K, accuracy)
# 添加文字说明
plt.text(K[arg_max], accuracy[arg_max], '最佳k值为%s' %int(K[arg_max]))
# 显示图形
plt.show()

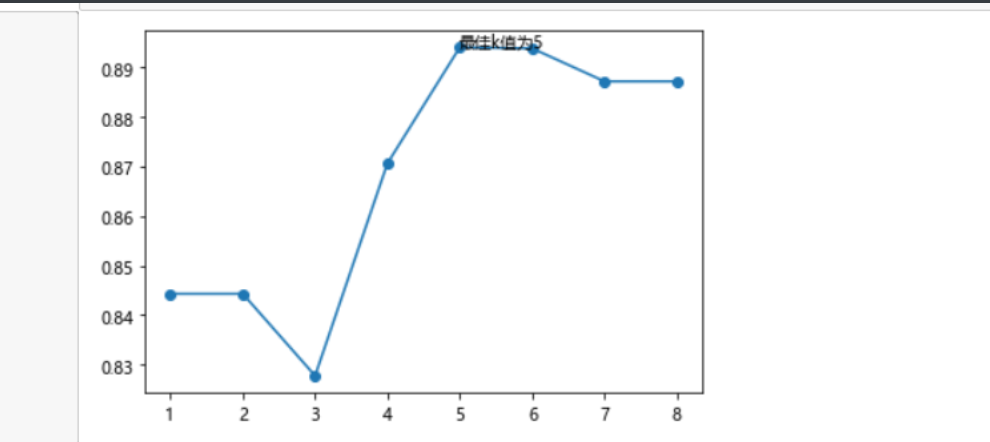
# 导入第三方模块
from sklearn import metrics

# 重新构建模型，并将最佳的近邻个数设置为6
knn_class = neighbors.KNeighborsClassifier(n_neighbors = 6, weights = 'distance')
# 模型拟合
knn_class.fit(X_train, y_train)
# 模型在测试数据集上的预测
predict = knn_class.predict(X_test)
# 构建混淆矩阵
cm = pd.crosstab(predict,y_test)
cm

# 导入第三方模块
import seaborn as sns

# 将混淆矩阵构造成数据框，并加上字段名和行名称，用于行或列的含义说明
cm = pd.DataFrame(cm)
# 绘制热力图
sns.heatmap(cm, annot = True,cmap = 'GnBu')
# 添加x轴和y轴的标签
plt.xlabel(' Real Lable')
plt.ylabel(' Predict Lable')
# 图形显示
plt.show()

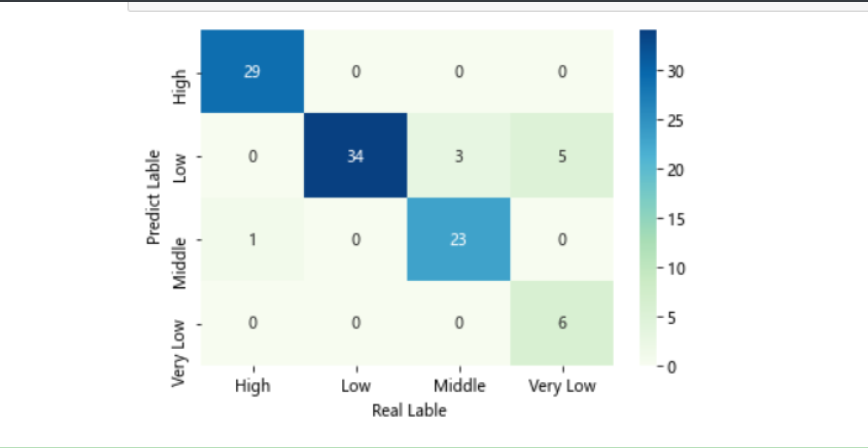
# 模型整体的预测准确率
metrics.scorer.accuracy_score(y_test, predict)
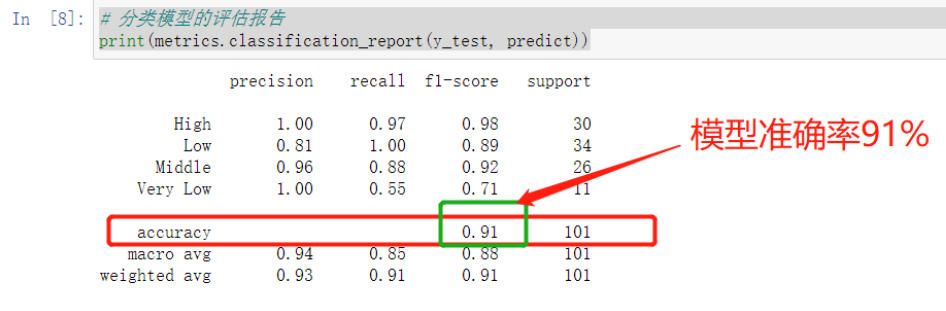
# 分类模型的评估报告
print(metrics.classification_report(y_test, predict))

CCPP小案例

# 读入数据
ccpp = pd.read_excel(r'CCPP.xlsx')
ccpp.head()
# 返回数据集的行数与列数
ccpp.shape
#################################################################
# 导入第三方包
from sklearn.preprocessing import minmax_scale
# 对所有自变量数据作标准化处理（统一量纲）
predictors = ccpp.columns[:-1]
X = minmax_scale(ccpp[predictors])
#################################################################

# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, ccpp.PE,                       test_size = 0.25,                                                 random_state = 1234)
# 设置待测试的不同k值
K = np.arange(1,np.ceil(np.log2(ccpp.shape[0]))).astype(int)
# 构建空的列表，用于存储平均MSE
mse = []
for k in K:
    # 使用10重交叉验证的方法，比对每一个k值下KNN模型的计算MSE
    cv_result = model_selection.cross_val_score(neighbors.KNeighborsRegressor(n_neighbors = k, weights = 'distance'), 
	X_train, y_train, cv = 10, scoring='neg_mean_squared_error')
    mse.append((-1*cv_result).mean())

# 从k个平均MSE中挑选出最小值所对应的下标  
arg_min = np.array(mse).argmin()
# 绘制不同K值与平均MSE之间的折线图
plt.plot(K, mse)
# 添加点图
plt.scatter(K, mse)
# 添加文字说明
plt.text(K[arg_min], mse[arg_min] + 0.5, '最佳k值为%s' %int(K[arg_min]))
# 显示图形
plt.show()

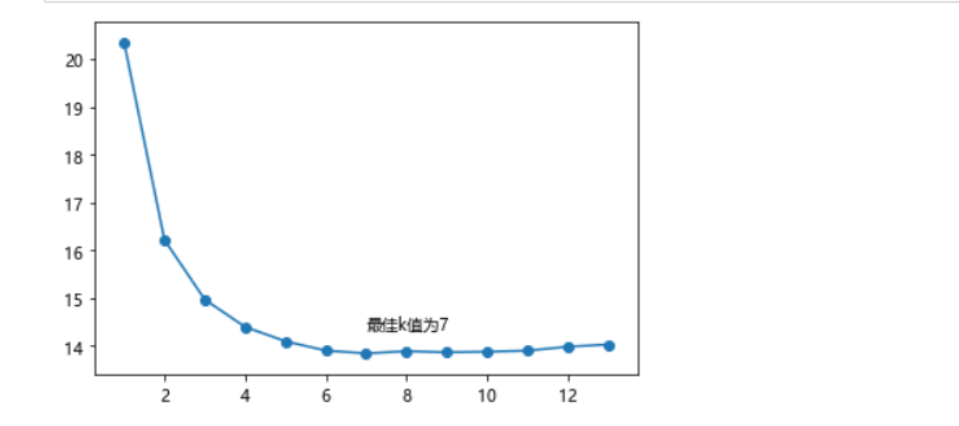
# 重新构建模型，并将最佳的近邻个数设置为7
knn_reg = neighbors.KNeighborsRegressor(n_neighbors = 7, weights = 'distance')
# 模型拟合
knn_reg.fit(X_train, y_train)
# 模型在测试集上的预测
predict = knn_reg.predict(X_test)
# 计算MSE值
metrics.mean_squared_error(y_test, predict)

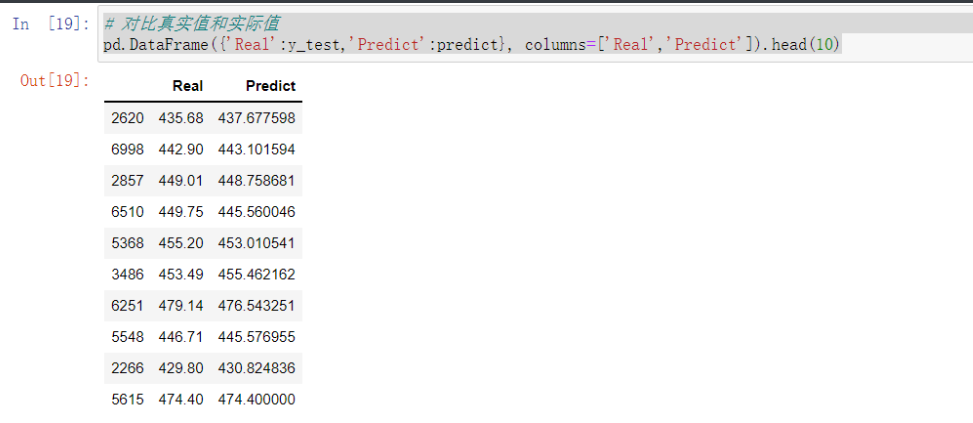
# 对比真实值和实际值
pd.DataFrame({'Real':y_test,'Predict':predict}, columns=['Real','Predict']).head(10)

# 导入第三方模块
from sklearn import tree

# 预设各参数的不同选项值
max_depth = [19,21,23,25,27]
min_samples_split = [2,4,6,8]
min_samples_leaf = [2,4,8,10,12]
parameters = {'max_depth':max_depth, 'min_samples_split':min_samples_split, 'min_samples_leaf':min_samples_leaf}
# 网格搜索法，测试不同的参数值
grid_dtreg = model_selection.GridSearchCV(estimator = tree.DecisionTreeRegressor(), param_grid = parameters, cv=10)
# 模型拟合
grid_dtreg.fit(X_train, y_train)
# 返回最佳组合的参数值
grid_dtreg.best_params_


# 构建用于回归的决策树
CART_Reg = tree.DecisionTreeRegressor(max_depth = 25, min_samples_leaf = 10, min_samples_split = 4)
# 回归树拟合
CART_Reg.fit(X_train, y_train)
# 模型在测试集上的预测
pred = CART_Reg.predict(X_test)
# 计算衡量模型好坏的MSE值
metrics.mean_squared_error(y_test, pred)


# 最终结果  16.17598770280405