树
1、树的定义:树是由n(n>=0)个结点组成的有限集合。
1.1、n == 0,称为空树;
1.2、n > 0,①根结点只有后继结点无前驱结点,②叶子结点(终端结点)只有前驱结点无后继结点,③非根非叶子结点(内部结点/分支结点)有且仅有一个前驱结点和两个或多个后继结点。
1.3、子树:除根结点以外的其他n-1个结点被划分为m(m>0)个互不相交的有限集合,每个集合又是一棵树,这些树被称为根结点的子树。
1.4、结点:树的基本单元,包含了结点数据块,指向孩子节点的指针域或父结点的指针域
1.5、结点的度:结点拥有子树的数量称为结点的度。
1.6、孩子结点:当前结点的所有后继结点
1.7、双亲结点:当前结点的前驱结点,所谓的双亲指的就是该结点的父节点(即代表父亲又代表母亲)
1.8、兄弟结点:继承自同一个双亲结点的一批结点被称为是兄弟结点
1.9、祖先:由根结点到当前结点的可达路径下,除当前结点外的所有前驱结点
1.10、子孙:继承自当前结点的所有子树中的结点均为当前结点的子孙
1.11、结点的层次/树的高度:指的是一个树中由根到最底层叶子结点所经历的结点层数
1.12、树的度:一棵树中所有“结点的度”的最大值
1.13、森林:多棵树组成一片森林
2、树的存储结构
2.1、双亲表示法:在结点中除了维护一个数据块之外还要维护一个指向双亲结点的指针域,各个结点(根结点除外)间将依靠这个指针域指向自己的双亲结点来维持一棵树状的数据结构,这种方式对于查找双亲结点非常方便,但是要查找孩子结点只能通过遍历整棵树了。
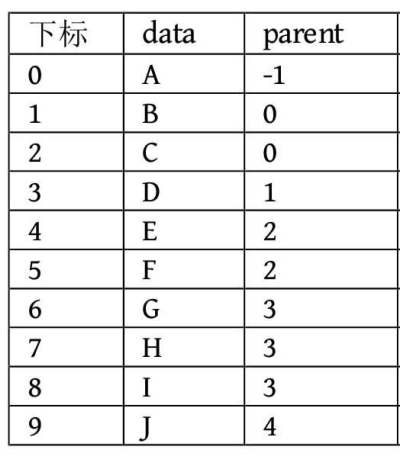
2.2、孩子表示法:在结点中维护一个数据块和其孩子结点的指针域,把树中的所有结点采用数组存储,数组中每个元素都对应一个结点。数组的每一个元素再链接着这个结点孩子结点链(从左至右排列)
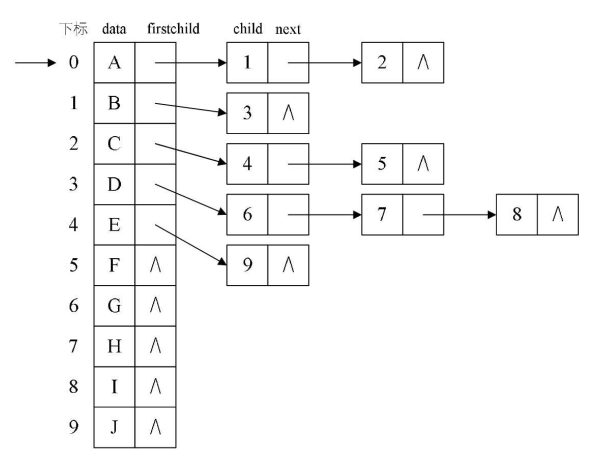
2.3、孩子兄弟表示法:在结点中维护一个数据块和其第一个孩子结点还有右兄弟节点指针域,这种方式可以通过firstNode进行纵向查询并且可以通过rightNode进行横向查询。
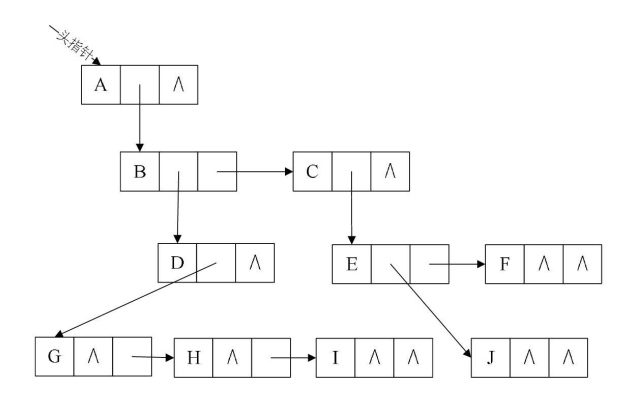
3、二叉树:是结点的一个有限集合,该集合要么为空,要么是由一个根结点和其两棵互不相交的子树(左子树、右子树)构成。
3.1、二叉树的五种不同的形态:
①为空的二叉树
②只有根结点的二叉树
③只有左子树的二叉树
④只有右子树的二叉树
⑤既有左子树又有右子树的二叉树
3.2、二叉树性质:
①若二叉树从第 0 层开始,则二叉树的第 i 层的结点数最多有 2^i 个。(i >= 0)——可采用数学归纳法证明
②高度为 h 的二叉树最多有 2^(h+1)-1个结点数。(h >= -1)——可采用等比数列前 k 项和的公式证明
③对任意一棵二叉树,如果其叶子结点(度为0)数为 n0 个,则度为 2 的非叶子结点数为 n2 个,则有 n0 = n2 + 1;
证明:n0(度为0,即叶子结点)、n1(度为1,只有一个孩子结点)、n2(度为2,有两个孩子结点)、n(总结点数)、e(总度数,即总结点数 - 1)
n = n0 + n1 + n2;
e = 2 * n2 + n1 = n - 1;
e = 2 * n2 + n1 = n0 + n1 + n2 - 1;
n2 = n0 - 1;
n0 = n2 + 1;
3.3、满二叉树:除叶子结点外的所有结点均存在左/右子树,并且所有叶子结点均在二叉树的最底层
3.4、完全二叉树:满二叉树是完全二叉树的一种特殊场景,其两者之间的区别在于完全二叉树的叶子结点可以不在同一层
①具有n(n >= 0)个结点的完全二叉树的高度(第一层 h = 0)为 h = log2(n+1) - 1;
②证明:设完全二叉树高度为 h (含有h+1层)
2^h - 1 < n <= 2^(h+1) - 1
2^h < n + 1 <= 2^(h+1)
h < log2(n+1) <= h+1
③特点:
(1)叶子结点只能出现在最底下两层
(2)最底层的叶子结点一定是集中在双亲的左部连续
(3)倒数第二层的叶子结点一定是集中在双亲的右部连续
(4)如果结点的度为 1 ,则只有左孩子,即不存在只有右子树的情况
(5)同样结点数的二叉树,完全二叉树的深度最小
3.5、二叉树的存储结构
①顺序存储:就是采用一个数组来存储二叉树的结点,运用特定的算法约束数组下标和结点之间的逻辑关系来维持二叉树的结构
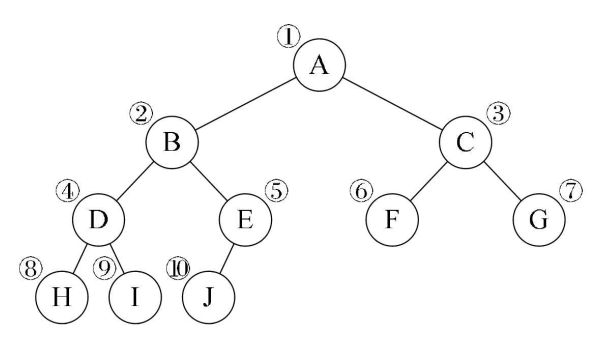
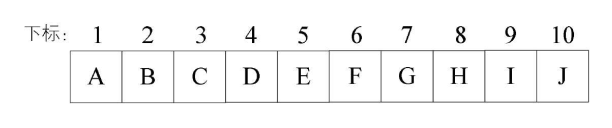
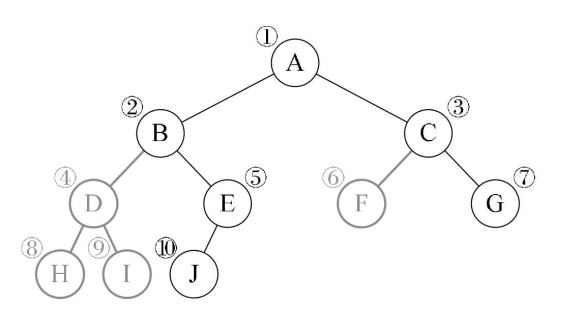
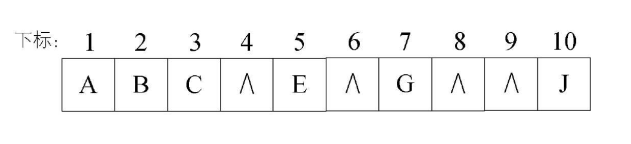
优点:采用数组的方式进行顺序存储与普通树相比,可以节省了每个结点因为孩子指针域的空间,内存空间连续,方便查找,但是对插入和删除操作需要移动内存空间效率不高
缺点:当二叉树是一棵极端的深度为 k 的斜树的情况下,也会造成数组的空间浪费
②链式存储:采用链表的方式进行维护二叉树结构,每个结点内部包括数据块、左/右孩子指针域三个部分,结点与结点之间依靠孩子指针域关联。这样的链表又称为“三叉链表”
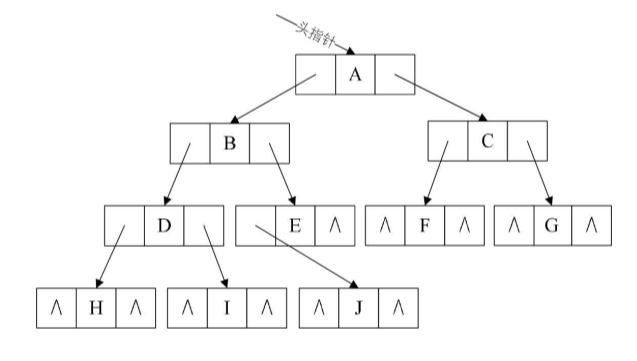
优点:单个结点在内存中分散存储,结点的插入和删除操作灵活,对内存的要求不高
缺点:由于分散存储的原因,所以在查询某个结点的时候需要遍历整个链表效率不高,每个结点需要维护孩子指针域空间浪费
3.6、遍历二叉树
①前序遍历:根结点——>左子结点——>右子结点
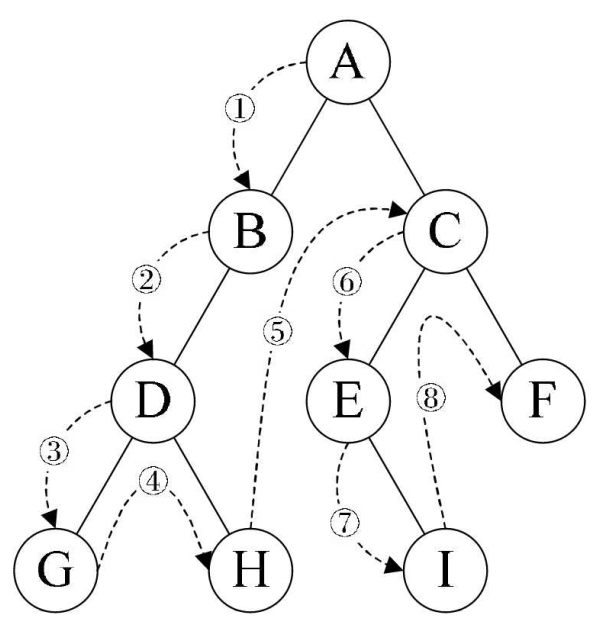
代码:
public void preOrder(){
System.out.println(this);
if (this.left != null){
this.left.preOrder();
}
if (this.right != null){
this.right.preOrder();
}
}
②中序遍历:左子结点——>根结点——>右子结点
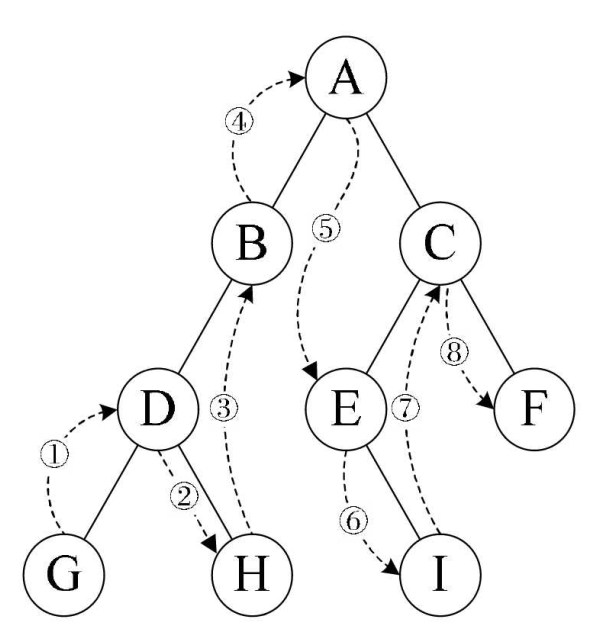
代码:
public void infixOrder(){
if (this.left != null){
this.left.preOrder();
}
System
if (this.right != null){
this.right.preOrder();
}
}
③后序遍历:左子结点——>右子结点——>根结点
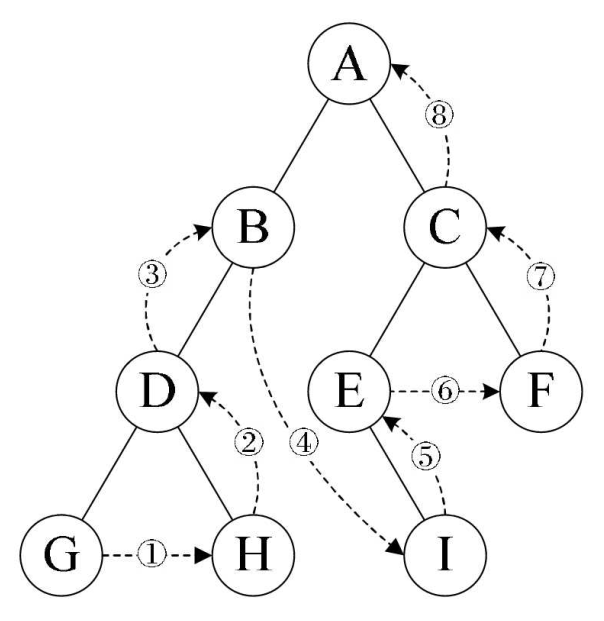
代码:
public void infixOrder(){
if (this.left != null){
this.left.preOrder();
}
if (this.right != null){
this.right.preOrder();
}
System.out.println(this);
}
④二叉树推导遍历结果:先找到根结点、区分左右子树范围。依次同样的操作递归左右子树
A:已知:前序遍历ABCDEF,中序遍历CBAEDF
解:由前序遍历规则可知根结点是第一个遍历出来的,找到根结点后再到中序遍历列表中区分出左子树和右子树(根结点的左边为左子树,右边为右子树),在各个子树中按照同样的规则进行即可。
B:已知:中序遍历ABCDEFG,后序遍历BDCAFGE
解:由后序遍历规则可知根结点是最后一个遍历出来的,找到根结点后再到中序遍历列表中区分出左子树和右子树(根结点的左边为左子树,右边为右子树),在各个子树中按照同样的规则进行即可。
3.7、删除结点
①规定:
a、如果删除的是叶子结点,则删除该结点
b、如果是非叶子结点,则删除该子树
②思路:
a、首先要考虑如果树为空树root,如果只有一个root结点,则等价将二叉树置空
b、因为二叉树是单向的,所以我们是判断当前结点的子结点是否为目标结点,而不能去判断当前结点是否为目标结点。
c、如果当前结点的左子结点不为空,并且左子结点就是要删除的结点,就将this.left = null,并且就返回(结束删除递归)
d、如果当前结点的右子结点不为空,并且右子结点就是要删除的结点,就将this.right = null,并且就返回(结束删除递归)
e、如果第2、3步没有找到目标结点,那么就向左子树进行递归删除
f、第4步没有找到目标结点,那么就向右子树进行递归删除
3.8、顺序存储二叉树
①顺序二叉树只考虑完全二叉树
②第n个元素的左子结点 2*n+1
③第n个元素的右子结点 2*n+2
④第n个元素的父结点为(n-1)/2
⑤n:表示二叉树中的第几个元素(按0号开始编号)
3.9、索引化二叉树(其实就是把二叉树转化称为一个双向链表的结构)
①介绍
a、n个结点的二叉链表中含有n+1 【公式 2n-(n-1)=n+1】 个空指针域。利用二叉链表中的空指针域,存放指向该结点在某种遍历次序下的前驱和后继结点的指针(这种附加的指针称为"线索")
b、这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种
c、一个结点的前一个结点,称为前驱结点
d、一个结点的后一个结点,称为后继结点
②索引二叉树思路(中序索引)
a、left 指向的是左子树,也可能是指向的前驱节点.
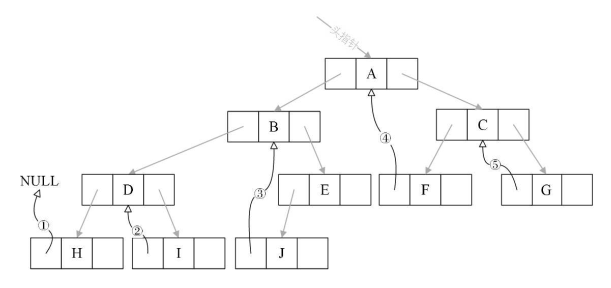
b、right指向的是右子树,也可能是指向后继节点.
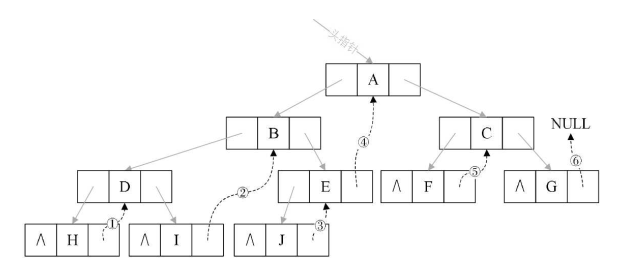
③实现步骤
1、如果node == null,不能线索化
2、先递归线索化左子树
3、线索化当前结点
①先处理左子结点
a、让当前结点的左子结点指向前驱结点
b、把当前结点的线索标识设置为1
②处理右子结点
a、让前驱结点的右指针指向当前结点
b、把当前结点的线索标识设置为1
4、递归线索化右子树
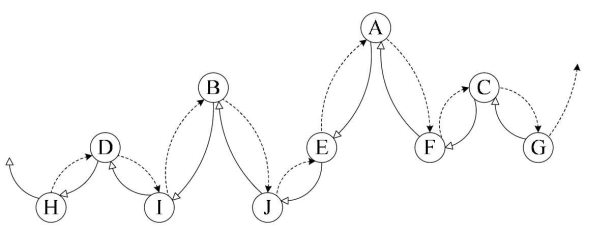
④优点:充分利用了空指针域的空间(相当于节省了空间),索引后的二叉树相当于一条双向链表的结构,所以具备双向链表的特性
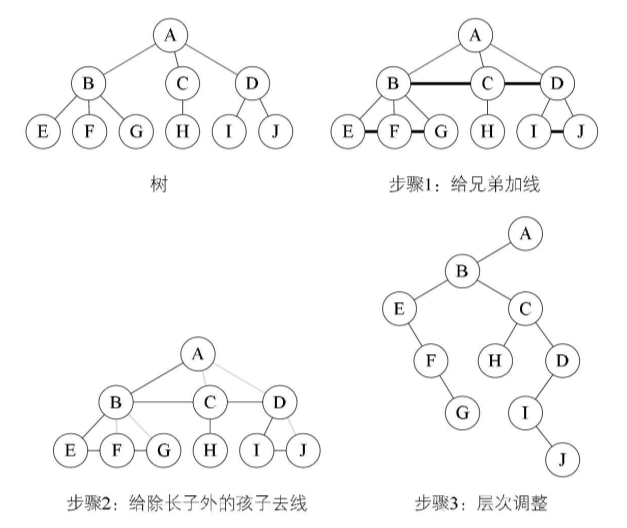
3.10、树 ——> 二叉树
①加线:所有兄弟节点之间加一条连线
②去线:对树中每一个结点,只保留它与第一个孩子结点的连线,删除它与其他孩子结点的连线
③层次调整:以根结点为轴心,将整棵树顺时针旋转45°。注意第一个孩子是二叉树的左孩子,兄弟结点均为该结点的右孩子
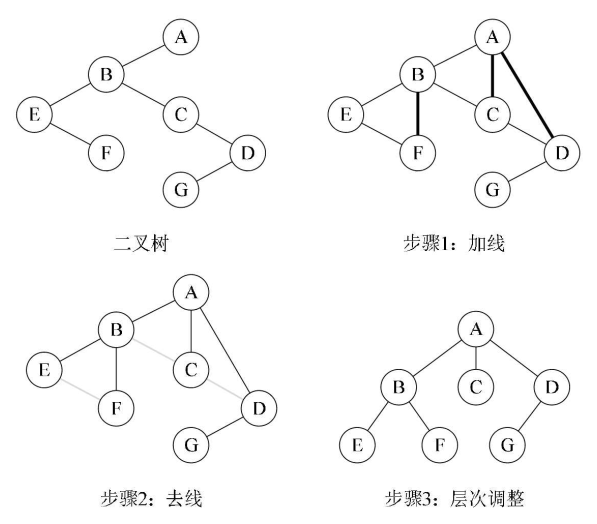
3.11、二叉树 ——> 森林
①加线:把当前结点的左子结点的n个右子结点作为自己的孩子结点,将该结点与这些右子结点进行连线
②去线:删除原来二叉树中所有结点与其右子结点的连线
③层次调整:移动各子树的角度使之层次分明
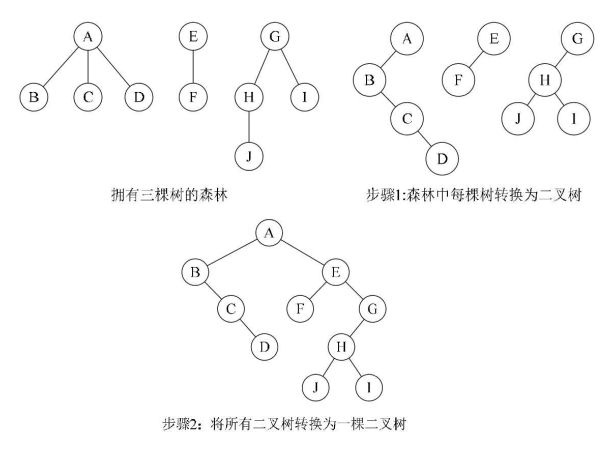
3.12、森林 ——> 二叉树
①把每个树转换为二叉树
②第一个二叉树作为原始森林,把其他二叉树依次作为右子树嫁接到第一棵二叉树的根结点
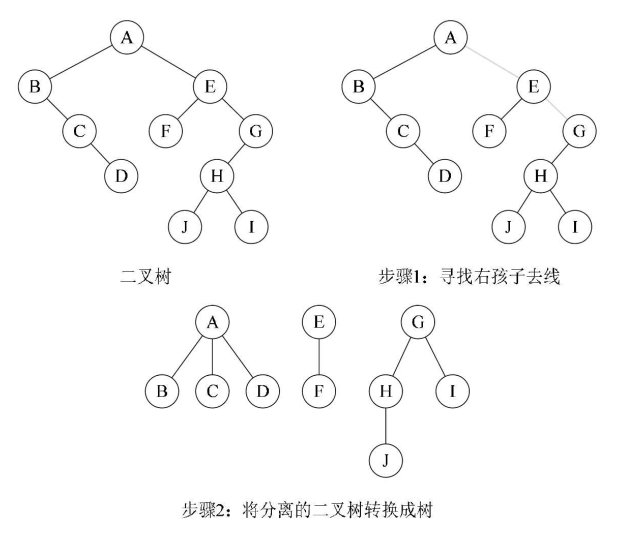
3.13、二叉树 ——> 森林
①从根结点开始若右孩子存在,则把与右孩子的连线删除。同样的操作递归所有子树,直到所有右孩子的连线均被删除为止,得到分离的二叉树
②将每一棵分离的二叉树转换成树即可
4、哈夫曼树
4.1、介绍:哈夫曼树又被称为最优二叉树,是由美国数学家哈夫曼博士创作。他的主要成就是研究出了哈夫曼编码,平时使用的文件压缩技术的原理是把待压缩的文件内容进行重新编码整理,以减少不必要的内存空间,而这一切都是源自最基本的压缩编码方法——哈夫曼编码。
4.2、定义:假设有 n 个权值[A5, E10, B15, D30, C40],构造有 5 个叶子的二叉树,每个叶子的权值是 5 个权值之一,这样的二叉树可以构造很多个,其中必有一个是带权路径长度最小的,这棵二叉树就称为最优二叉树或哈夫曼树。
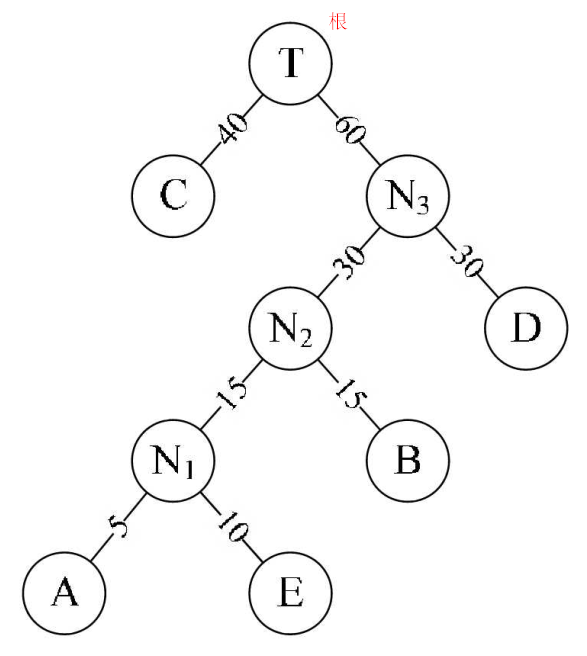
4.3、路径:从一个结点到另一个结点之间所经过的所有结点,被称之为两结点之间的路径(N3~A,N3->N2->N1->A)
4.4、路径长度:在一棵树中,从一个结点到另一个结点所经过的“边”的数量,被我们称为两个结点之间的路径长度(N3~A,3)
4.5、结点的带权路径长度:从根结点到该带权结点的路径长度 L * 权重 W(A,4 * 5)
4.7、构建哈夫曼树
①根据给定的 5 个权值{5, 10, 15, 30, 40},构成 5 棵二叉树的集合(排序规则:根据结点权值升序排列) F = {A5, E10, B15, D30, C40},其中每一棵二叉树只有一个带权值的根结点,其左右子树均为空
②在 F 中选取两棵根结点的权值最小的树作为左右子树构建一棵新二叉树,新二叉树的根结点权值为两个子结点权值之和
③删除 F 中被选中的两棵树,同时把新二叉树的根结点插入到 F 中(注意排序规则)
④重复 ② 和 ③ 步骤,直到 F 集合为空为止,构建完成的树称为哈夫曼树(最优二叉树)
4.8、特点:
①没有深度为 1 的结点
②n 个叶子结点的哈夫曼树共有 2n-1 个结点
③哈夫曼树任意非叶借点的左右树交换后仍是哈夫曼树
4.9、时间复杂度:O(nlogn)
4.10、代码
package com.suancloud.lcy.tree; import com.suancloud.lcy.sort.HeapSorting; import java.util.ArrayList; import java.util.Comparator; import java.util.List; /** * Author: chaoyou * Email:1277618785@qq.com * CSDN:https://blog.csdn.net/qq_41910568 * Date: 2020/4/15 0015 12:07 * Content:模拟哈夫曼树 */ public class HuffmanTreeDemo { public static void main(String[] args){ int[] data = {5, 10, 15, 30, 40}; HeapNodeUtil nodeUtil = new HeapNodeUtil(); ArrayList<HeapNode> heapNodes = new ArrayList<>(); HeapNode node = nodeUtil.buildHuffmanTree(heapNodes, data); node.preOrder(); } } // 哈夫曼树的工具类 class HeapNodeUtil{ /** * 功能需求:设计一个根据给定的 5 个权值{5, 10, 15, 30, 40},构成 5 棵二叉树的集合(排序规则:根据结点权值升序排列) F = {A5, E10, B15, D30, C40} */ public List<HeapNode> buildMinHeap(List<HeapNode> list, int[] data){ int[] ints = HeapSorting.heapSorting(data); for (int num : ints){ list.add(new HeapNode(num)); } return list; } /** * 功能需求:设计一个删除结点列表中权值最小的结点,并返回该结点 */ public HeapNode deleteMinWeigth(List<HeapNode> heap){ if (heap.isEmpty()){ return null; } HeapNode remove = heap.remove(0); return remove; } /** * 功能需求:设计一个把新结点插入到结点列表中的方法(完成权值排序) */ public List<HeapNode> insertNode(List<HeapNode> heap, HeapNode node){ heap.add(node); heap.sort(new Comparator<HeapNode>() { @Override public int compare(HeapNode o1, HeapNode o2) { Integer o1Weight = o1.getWeight(); Integer o2Weight = o2.getWeight(); return o1Weight.compareTo(o2Weight); } }); return heap; } /** * 功能需求:设计一个构建哈夫曼树的方法 */ public HeapNode buildHuffmanTree(List<HeapNode> list, int[] data){ // 根据给定的 5 个权值{5, 10, 15, 30, 40},构成 5 棵二叉树的集合(排序规则:根据结点权值升序排列) F = {A5, E10, B15, D30, C40} List<HeapNode> heap = buildMinHeap(list, data); HeapNode node = null; int size = heap.size(); // ②在 F 中选取两棵根结点的权值最小的树作为左右子树构建一棵新二叉树,新二叉树的根结点权值为两个子结点权值之和 // ③删除 F 中被选中的两棵树,同时把新二叉树的根结点插入到 F 中(注意排序规则) // ④重复 ② 和 ③ 步骤,直到 F 集合为空为止,构建完成的树称为哈夫曼树(最优二叉树) for (int i=1; i<size; i++){ node = new HeapNode(); node.setLeft(deleteMinWeigth(heap)); node.setRight(deleteMinWeigth(heap)); node.setWeight(node.getLeft().getWeight() + node.getRight().getWeight()); insertNode(heap, node); } return deleteMinWeigth(heap); } } // 构造一个哈夫曼树结构类 class HeapNode { private int weight; // 每个结点的权值 private HeapNode left; // 左子结点 private HeapNode right; // 右子结点 public HeapNode() { } public HeapNode(int weight) { this.weight = weight; } public HeapNode(int weight, HeapNode left, HeapNode right) { this.weight = weight; this.left = left; this.right = right; } public int getWeight() { return weight; } public void setWeight(int weight) { this.weight = weight; } public HeapNode getLeft() { return left; } public void setLeft(HeapNode left) { this.left = left; } public HeapNode getRight() { return right; } public void setRight(HeapNode right) { this.right = right; } /** * 功能需求:设计一个二叉树的前序遍历方法 */ public void preOrder(){ if (this == null){ return; } System.out.println(this.weight); if (this.left != null) this.left.preOrder(); if (this.right != null) this.right.preOrder(); } @Override public String toString() { return "HeapNode{" + "weight=" + weight + ", left=" + left + ", right=" + right + '}'; } }


