24.7

这段时间都没打题，切腹

7/8

打完比赛后感觉脑子shi了
吃饭的时候差点睡着
不过我每天都很困来着

T1

显然，讨论一下A=0 B=0 等等情况

代码：
没看见所有人都必须要有水果 要判n>2A+B
输出-1之后忘return
2A+B爆int了

做题：
注意所有条件！

T2

显然，字符串都可以用[i,j]表示
先 O(n³) dp一次处理代价
再 O(n³) 转移

T3

考试的时候理解错题意了

首先，边数<16 -> 块数顶多7

因为图的性质，就先考虑了一下竖着分割
从下往上考虑，出现下面有竖线、但上面无故截断了的情况肯定不优（下面那条线就可以删去/移走了）
但这个软用没有

不考虑怎么做最优，而是怎么做不优，成为限制条件，优化枚举
比如这里，一个很显然的感觉就是要每个矩形尽量大，但实际上很难想
结合图的性质，考虑每个上边向下向两边扩展，对于冲突的部分指定优先级
考虑枚举块的顺序，依次进行最大扩展，暴力求最优解

代码:
最开始卡了很久，觉得n=7很小随便写就行了但又想不出好写的
最后暴力涂色暴力数，其实不难写

做题：
写代码的时候不要执着于很优美的做法
时间复杂度以内，思路简单、变量直接 的更好写

吃饭去了
过会把 T4、凸包和 写了

T4

诶嘛真难搞

首先容易发现P的意义：
二进制cnt(1)&1
二叉树bfs(这个没啥实际意义)
由0/1扩展（这个想题的时候很难证确切）

然后我就开始乱搞了什么也没搞出来

用二进制，发现一段P序列满足在2^k次前后有微妙的对称性，再一看是P0/1的前缀
充分必要法证明性质：
先证P->切割点
再证切割点->P

但是一段序列可能有不止一个切割点
先考虑两个切割点：发现切割点之间必须是2^k
再考虑三个切割点：拿二进制来理解，很容易发现不存在

所以计数：枚举切割点-枚举两个切割点

注意：
两个切割点时（i，j)，j处的P肯定和i的0/1不同
但i前面那半段rev()后的P是和k相关的

7/9

空间开炸了，挂分75，望周知

T1

简单高中数学题
算一下，有循环节（长度为3）

OI做法：
用 p/q 表示结果，f(x) 可矩乘转移

T2

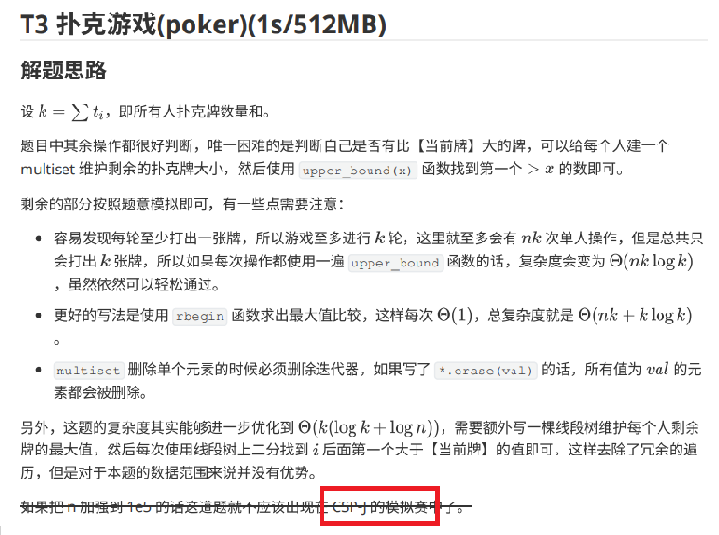
T3

题解做法：
找到 a 的严格前缀最大
令其中相邻两个点为 L、R
由于 R 之后的那个区间里的数都小于aR，满足2-0
L-R中间就不能有1-2(R)

猫の做法：
发现性质，建立笛卡尔树
对树的形态计数
一个tip ： 序列计数的时候把 a[i]+=i 就可以 不降 <-> 单调增

我：
因为只有比较，所以记相对排名
然后在末尾插入
由于 1-2-0，所以记录最大的 1，插入时要比ta大
显然的可以差分

\(O(N^2)\) : 二元生成函数

所以这场比赛真的是普及组难度……

代码：

快速幂的log也是复杂度！并且常数比较满！不能忽略！！！

T4

本题“略微超出了普及组的难度”
QAQ那我是什么，小垃圾吗

不要执着在一个性质上 想了5min+后还没头绪就可以先放着想想别的
然后找最简单直接的那个写

70pts做法：
简单初中几何题
根据 \(S=\frac{1}{2}absinC\) ，当 a、b 已知，c² 尽量贴近 a²+b² 即可
但是数组开太大，一分没有

浪费我半天时间的性质：
\(16S^2=2(a^2b^2+a^2c^2+b^2c^2)-(a^4+b^4+c^4)\)

\(std\) : 分治

一个优化：
已知 a, b<a，那么 b 越接近 a 越好（显然）
对于 a, b>a，依然只用考虑最接近 a 的 b
证明：不是 ( a , b2 , c ) > ( a , b1 , c )，而是 ( a , b2 , c ) < ( b1 , b2 ,c )
启示：不一定要直观地证明【2】劣于【1】, 只要找到【1'】即可

所以分治时可以直接拿到左边的 a , b ，应用秦久韶公式放到李超线段树上（常数很小，放心使用），再对于右边的 c 查询

所以我和 AK 一场 CSP-J 模拟赛之间也没差多少，就漏了一个性质
启示：想到的方向可以先放着，但不要扔
首先你的脑子想不出太多性质了，其次 CSP-J 模拟赛不会这么难的
或者理解不了的大条件析出几个小条件然后理解透

代码

1.数组开太大了
2.分治注意顺序，这里由于f是与前面相关的，所以是左中右的顺序

李超线段树时间复杂度

换了写法，时间复杂度就很显然了
每一层只向一个区间递归

void insert(int &p,ll l,ll r,line v){
    if(!p) p=++ns;
    if(v.gt(mid)>=c[p].v.gt(mid)) swap(c[p].v,v);//mid: v<=pv
    if(v.gt(l)>c[p].v.gt(l)) insert(lc,l,mid,v);
    if(v.gt(r)>c[p].v.gt(r)) insert(rc,mid+1,r,v);
}

数论

gcd

gcd(a1,a2,...,ak)=gcd(a1,a2-a1,...ak-ak-1)
可用于修改区间加，询问gcd
这样就可以区间加转化成差分惹

欧拉定理

条件是 a,p 互质

exgcd

不用记，按gcd的方法现推即可
枚举所有解：x0=y/d,y0=-x/d

• 证明：
  • x0 y0 -> x y：显然
  • x y -> x0 y0：反证法 ？

数据：exgcd ( a , b , x , y ) 解出来的 x , y 在 [ -a/-b , a/b ] 范围内

扩展中国剩余定理

为什么不讲中国剩余定理，因为没用

两个方程列等式用exgcd解，化成一个

\(x=a+bp=c+dq \Rightarrow bp-dq=c-a\)
之后有 \(x=a+bp \pmod{lcm(b,d)}\)
因为 p 一次变化 d ，所以 $ \pmod{lcm(b,d)} $ 下的 x 只有一个

卢卡斯定理

\(C(n,m)=C(n\ mod\ p,m\ mod\ p)\ C(n/p,m/p) \pmod p\) ( p 为质数)

特别的，当 𝑝 = 2 时，C ( n , m ) = [ n & m == m ]
另一个优化: C ( n , m ) 在 n < m 的时候为 0 ，不用再算了
事实上要算的次数理论上很小，考虑 C ( n , m ) 的公式即可

应用的更多的时扩展卢卡斯

原根

第一次学，做完题再敲字

求原根：
虽然不理解，但是直接枚举+判定即可 复杂度为\(O(p^\frac{1}{4})\)

7/10

T2

T3

容易想到二分答案，判断是否可行（状压即可）
时间复杂度 \(O(n2^k)\)

但是对于任意一个 f [ i ] [ s ] = 1 / 0 合法 , 之后的 f [ j ] [ s ] ( j>i ) 都合法
也就是说这个状态非常冗余，可以转化为 f [ s ] 表示 s 第一次合法的 i

详细地，枚举状态 s
因为 f [ s ] 记录了 s 的最先的 i
可根据这个记录值转移出 f [ s | 1<<k ]

启发：
优化DP树的思想，关联状态合并表示

代码：

考场上
1.数组越界
2.不知道为什么转移位置的下标状态写错了
订正时
1.最开始想的是对于 k 种转移，记录一下所有合法且没做过的 s （ 对应的 t 没有）
$\ \ \ $但这样写真的很麻烦，而且记录/删除多个log
2.数据类型开错/数据维度开串 -> 先写主题代码后开变量，当值全为01的时候可能是因为它只能是01
3.数组维度写反... 写代码的时候脑子带上

T4

考场思路：
按 dfn 序对区间排序
答案就是所有 de[] - 相邻 lca 的 de[]

思路1：
将 a 离线，枚举 r，依次染色
每次从 ai 向上染色 i 直到根节点（如果原有颜色，直接覆盖掉）
那么如果树上的某点颜色小于 l ，肯定不在区间里
经行树链剖分维护即可

思路2：
对于 [ l , r ] 考虑每个点的贡献
则有贡献的点 u 应满足
1.在 [ l , r ] 的最大子树内
2.对于点 v，令 a_x = v ，将 u 子树内的 x 排序，不存在 xi < l < r < xj
若 u 在 [ l , r ] 的区间外，发现显然有 l , r 不在 x 中
也就是只有 u 在 rt 内时，条件 2 才可能不满足
所以直接 sz [ rt ] - count[ xi < l < r < xj ]
计数转换成矩阵 扫描线 ： 区间修改单点查询

代码：
n、m写混
而且只检查了一个部分分的代码

树上时间复杂度！

1.背包合并时严格处理两个背包上界
2.时间复杂度：sz 等价于 结点，转换为对于每个点，ta参与的合并的时间复杂度贡献

\(O(N^2)\)

sz -> 点，考虑意义
那么每两个点只会在 lca 处转移一次

\(O(NM)\)

对于 sz [ u、v ] < m 的点，显然有这样的子树最多 n / m 棵
对于 sz [ u ] < m , sz [ v ] > m ， 进行 sz -> 点的转化，那么每个点只会在向上时经历一次这种 u ，复杂度依然为 O ( n m )
对于 sz [ u、v ] > m ，等价于合并最多不超过 n / m 次，每次 m²

\(O(\frac{NM^2}{log_M})\)

n 个点，每个点都有价值、体积，体积上限为 m
按上面的方法一样来一遍推理可得

本题还有更加优秀的复杂度，那是另外的话题了

---

吃完晚饭回来想着趴一会
结果直接睡了一个多小时
淦（ 打这段字的时候依然困得要死 ）
今天 9:30 保证睡

---

从睡醒到现在一直在 emo
感觉活着好累，不想活了

---

现在不困了。但是产生了新的困扰
下辈子愿做一颗不用睡觉不用社交的树

7/11

T1

考虑到边权只有0/1，01BFS 即可
可以 O ( n ) 模拟

T2

想思路的时候卡了一下

观察 x ^ i ，因为 i = [ 1, 2ⁿ ] ，那么 x ^ i = [ 1, 2ⁿ ]
也就是可以把 ^ x 的操作理解为将 a 中的值互换位置 ，取后 k 个 a [ i ]

再看 x ,异或操作是可以叠加的，不妨按位考虑
如果 x 的第 k 位为 1 ，就是把所有 2 ^ k 的块交换

k 从高向低考虑，对于当前最高位，只有两块
取靠右的 q 个，连续，那么发现显然只需要两块 q % ( len/2 ) 的值
总之可以递归求解

代码：
1.快读快输
2. dfs 改递推
但是本地大样例跑了 59 s , 交上去却 AC 了该怎样 ？

T3

观察数据，分析 n 为奇数情况
想到枚举 gcd 的结果 x
构造 ( kx , n ) 使其等于 x
对于一个质因子 p , 设 p^c1=k , p^c2=x , p^c=n
那么有 min { c1 + c2 , c } = c1
当 c1 = c 时， c2 任意
反之 , c2 = 0 ，也就是 k 不含 p

然后 k 的个数的求法类似于求 \(\varphi(n)\)
就是 $ N\prod \frac{p-1}{p}$

T4

首先 k = 1 是 原题
就是对于每个 u 处理和 ta 联通的点数
考虑建虚树，所有有贡献的链一定恰好一个端点在 u 内 / 或者链的顶点在 u 上
dfs 遍历，加入链/删除链，子节点向上合并维护线段树
那么这题是 动态开点 + 线段树合并 的

然后 k > 1
由于 k n 较小，所以考虑从 1 、 k - 1 转移到 k
设和 u 距离为 k 的点集为 \(P_k(u)\)
那么则有 $P_k(u)=\sum_v [w\subseteq P_1(u), P_{k-1}{v}] $
我们对于已知的 u , v 考虑 w 满足的性质，发现如果存在这样的 w ，其必然构成形状为树连通块
可以用 \([s!=\emptyset]=|V|-|E|\)判定，V 是满足 w 条件的点集，E 是两个端点都满足 w 条件的边集
也就是转化成 \(P_k(u)=\sum_v |V|-|E|\)

你会觉得这不是智障吗？
但是我们再一看，发现 |V|-|E| 显然是可以拆开的！ 所以枚举 v 的限制就不存在了！
\(\sum_v |V|=\sum_{dis(w,u)=1} |P_{k-1}(w)|\) ，因为 w 会被 \(|P_{k-1}(w)|\) 个 v 枚举到
对于边 e(x,y) 定义 \(Q_k(e)=\sum_u [ max\{dis(x,u),dis(y,u)\}<=k]\)
\(\sum_v |E|=\sum_{dis(e,u)=1} |Q_{k-1}(e)|\)

但是 \(Q_k(e)\) 怎么求呢？
相信如果你真正理解了 \(P_k(u)\) 的求值方法，还是可以顺下来的

所以我敲不动代码了

7/12

T1

观察样例，发现有 r 取值相同
所以考虑一下取值一样的情况
因为计算式是一元二次，所以只有一个极值点（显然），令其为 k
对于相邻两个 k1 < k2 ，显然就是要让 r1=r2 的，也就是可以把两个二次式合并成一个
用栈去做即可

代码：
n , m 又写反了 ！

• 以后写循环时在脑子里过一遍枚举什么
• 检查的时候看一下每个变量被用到的地方，比如记录、读取，缺失的话就是哪里打错了

T2

WQS 二分：
首先凭感觉发现 f ( m ) 上突，（ 随着 m 的增大，增数递减 ）
也就 f 图像上的斜率是单调的
对于斜率 k ，做、作过 f 的线，考虑 ta 的截距：g ( x ) = f ( x ) - k x
显然过切点的那条直线截距最大，假如你可以轻易地求出 g 最大时的 x ，你就可以知道斜率 k 对应的切点了
二分 f ( m ) 的斜率，得到对应的 g ( m ) ，可得 m
总结一下：
1.状态限制 -> 代价计算
2.随着状态限制的变化有单调变化

随机乱搞：
显然对于 f [ i ] ，能对 f [ n ] [ m ] 做贡献的 [ j ] 不多

代码：
做完之后造数据验证了一下，但是写的是 rand() ，世界上最假的随机函数
成功自己卡掉自己，浪费一个多小时
下辈子一定要用 mt19937 rnd(time(NULL)) 和 rnd()

T3

图相关的知识真的不够，补补补！

首先对于一棵树的形态，考虑黑白染色，并将黑点取反
这样一条边两端 + v 就转化为一段 + v 一段 - v，限制条件就变得清晰，一段连通块的 S 不变，任意分配

对于有环
发现偶环照样是黑白染色
但是存在奇环的连通块就可以任意加减，限制变成 S 的奇偶性不变，对每个连通块进行判定即可

这样的题做过啊，考场上怎么没想出来
以及以后多做图的题

代码：

1. += 写成 =
2. 当你的函数有多个功能的时候，不要随便 break
3. 染色染 0 / 1 但是判断是否染色用的是 col[x]!=0 -> 改过来之后忘了改另外一个存颜色对应和的数组

T4

此题差点被 sxt AK，望周知
6：00 订正掉！ 结果是6:18

思路：将 ( x , y ) 的两个限制放到两棵重构树上简单维护

先考虑一个端点时最值的限制，也就是对于一条链，左/右端点分别时最大最小值
sxt 有云：树上的路径是很难做的，但是 向下的一条链 是很简单的
重构树：
先找出当前树上最大点

• 不会有越过它的链，因此和这个点连的边都可以不要管了
• 这个点 以其他所有点为另一个端点 构成的链，必然满足限制

所以以此点为重构树的根，可以满足所有 根-子关系 都符合条件，谁是根的亲儿子无关紧要
然后对于断开边的几个连通块，分别建树，rt' 和 rt 相连
我们建这样两棵 max 树 / min 树
那么显然，一段满足条件的（ x , y ) ， x 、y 在两棵树上都有直接祖先关系
对于这两棵树计数即可

对于第 1 棵树，利用 dfn序 维护 u 的所有子结点
对于第 2 棵树，利用 dfs 时的链维护 u 的所有父节点

代码：

不知道为什么看着样例写代码，于是把 n 写成了样例中的值 7

7/13

T1

发现 "连边" 相对于 "求连通块" 信息过多，考虑特殊情况：质数、2

T2

根据题意推导，h [ i ] [ j ] 的取值范围为 [ i + j - 1 , i + j ]，仅 0 / 1 两种，考虑 0 1 矩阵的性质，发现可以简化为不互相覆盖的 +1 点
再根据已知的 h 得出合法 +1 点的范围，然后转移

T3

先考虑合法的不染色方案，比如两个点和同一条边相连，边数只有 6 ，很小
考虑在二分图上构造这种情况，顺便就可以排掉其他不染色方案的可能了

二元环计数一个 trick ：n m 同阶 -> 每个点摊不到多少边 / 边数大的不会有几个，做法有些度数相关有些点相关 -> 根据度数根号分治

代码：没考虑鸡爪型

T4

| x - y | 转化为移动距离
先放宽条件，转 “=” 为 “>=” ( 只上移即可 )，再缩条件，就是在合法的情况下移
发现（ l , r , v ) 之间根据 v 有严格优先关系，v 相同时 DP 转移

代码：后面写 DP 的时候急来了。简单直观、复杂度以内可不必专门考虑数据结构
可删堆：维护两个 q1（存）, q0（删），查询 q1 时对一下 q0 的 top()，不重的话无影响

发现直接做很难维护
考虑拆累乘的式子

翔哥有个错的做法，但感觉思路有借鉴意义

7-14

炸 100 pts

T1

用 b 构造路径，如果 u - > v - > w 的路径重复走，v 就一定是一个终点

代码：这段时间第三次了。想思路时不必求复杂度简单无数据结构。简单、正确性显然为上。

T2

听说这个叫猫树。但是 sxt 有云：不要把思维局限在学不完的算法里，而是拆解成灵活的 trick

背包全部合并是 O(k^2)，考虑到答案只求单点，尝试着每个 qry 只合并一次 O(k)
对于 合并点 m，背包的前缀后缀都需要 O(nk) ，考虑重复利用 m , 线段树形分治即可

线段树形分治：logn 层，每层 2 ^ k 个拆分点。利用 [ l , r ] 之间的重复， 左右中/左中右 地处理

T3

有效的值只有三种 >1 1 0 ，如果一个个删就需要记录所有值
考虑多个区间的一段重复部分，这一段总值只有在 0 / 1 的时候才可能改变答案，这样就把多个区间的 [ l , r ] 的状态压到一个点的 cnt 上
于是线段树形分块

T4

7-15

T1

思路：
发现答案只有 0 1 2 ，判断 1 就是是否有点为必经点
trick : 分别记录 S -> u ，T -> u 的情况数，必经点 <-> 两段乘起来就是总方案数

代码：
循环：l r , n m 写反

T2

思路：
发现 a b 值域不同，而 gcd 的值是取 min 的，除去全为 b 的仅一种情况，可缩小 gcd 值域
对于 gcd 考虑合法 ， 那么取 a 时条件显然，关于 a 考虑 b , 即 \([\ gcd_{a\%d!=0} b\ \% d = 0\ ]\)
那么把所有 b 按照 a 存起来，对于一次 d 查询 O ( V / d ) 区间gcd 即可

代码：
多换行，每行想清楚思路再写
记混变量意义 -> 调用时想一下
循环：变量类型不符，i##end(r) 会爆

T3

思路：
考虑对 dis 计数，然后找第一个 s [ dis ] >= K 的
发现对于路径为 1 ，计数不需要在后面加，而是可以从 len/2、len-len/2 分两半转移
路径 > 1 , 考虑拆边，为保证起点终点都是真点，建立虚点向真点连边

T4

7-16

T1

区间操作 -> 差分&单点

T2

考虑暴力剪枝，发现由第一行可以确定全局状态，判断最后一行即可
建立方程表示结果与操作序列的关系，高斯消元+bitset优化

代码：
建立方程/算式子时，尽量避免手写找规律，容易错&码风丑

T3

容易建网络流，发现二分图
只用判断完全匹配 —> 对于一边的点集 \(A\) 和对应的匹配 \(S_A\) ，都有 \(|S_A|>=|A|\) 即合法
trick : 密集的必要条件 —> 充要条件
所有性质、推论的推论都要考虑可优化的点，分析目的和过程，但一个性质 5min 左右还没头绪就可以放了

代码（赞美 sxt ）：
1.可以预处理的部分放在二分里每次做一遍
2.数组开小，T了

T4

对于一条以 x 为顶点的路径，分成两部分：与 x 相关 ( w1 )、与 x 无关 ( w2 )，两部分都和链两端的深度有关系，考虑到深度较小，暴力枚举 d1 d2
最开始想的是根据 x 判断有无解，但 d1 d2 确定的情况下 w2 的值不连续
\((2^{d1+1} + 2^{d2+1} − 3) \times x + 2^{d2} − 1 + w2 = S\) ,又有 \(w2 < (2^{d1+1} + 2^{d2+1} − 3)\)，x 只要是正整数
考虑对 w2 判断有无 x。可推出 w2，尝试构造

代码：
每向右拐增加 2^k-1 ，很难做，所以再枚举加了多少个 2^k-1，把 1 补回去
dp : f[x][y][0/1] 表示处理完第 x 位，加了 y 次，当前位还需不需要 1
顶点 x > 0 ，要判断超界

高维前缀和

trick : 令 x 补集为 [x] ，有

• x | y = x + [x] & y
• x & y = x - [ [ x ] | y ]
• x ^ y = x | y - x & y

7-17

T1

诈骗题：考虑拼接，计数码和为 n ，就是构造 m | k n，k 取 m 即可

做题：把条件列清晰

T2

思路：

1. 概率x1 <—> 期望，所以转为设 E(x) 表示经过 x 的期望次数，做了无限次后 { E } 可以认为不变
2. 考虑从别的维度设置状态/值：f(x) 表示初始拥有 x 个筹码输掉的概率

做题：列清楚全流程后再写

T3

被暴力碾压了（泣

思路：
列出判断点 k 是否满足直线的方程，发现同样可以用 点k 相关的一次式判断直线
每次直线判点都要逐步向右扩展，有重复。整体处理+下放：对于直线集考虑 [ l , mid ] 中是否有符合条件的点 ，每条直线下放 logn 次

代码：
条件含大于小于，必须保证精度，手写 p/q
清空线段树要删掉rt

T4

经典 trick : 排序/中位数 -> 01序列，本题枚举所有 01序列即可
排序操作会把很多 01 排列归为同一种状态，考虑边枚举边排序，对于第 x 种操作枚举排序后的状态，只跟操作覆盖了几个 1 有关
如果所有操作不能把区间全覆盖认为无解，每次枚举新覆盖到的区间的 1 的个数（设为 \(d_i\) )
时间复杂度常用 trick : 如果满足$\sum d_i = n $ ， $ O(\prod{d_i})$ 在 $ d_i $ 全取 $ e $ 时最大，\(d_i\) 整数时取 \(3\)，\(n\) 在 \(50\) 以内即可 。但本题 \(q\) 较小，所以直接摊 $ O((\frac{n}{q}+1)^{q}) $
乱搞 trick ：随机一些状态检测即可，可在绑定数据中获得 80pts 的好成绩

代码：小心变量写错 -> 打一段查一次
乱搞: clock()<900

随机

随机数据的常用结论：

1. 状态转移形如从 ( 1 , 1 ) 划折线到 ( n , m ) 时，通常只用枚举 [-B,B] 的一段
2. 共有 n 种物品，每次均匀随机地从中选取一个，全选过的复杂度为 \(O(nln^n)\) 级别

期望概率のtrick

有终止无次数限制：

1. 无限次后遍历某状态的期望次数不变，列方程
2. 和终止点的距离（找性质，一般不直观）

鞅与鞅的时停定理：

感觉这辈子都用不到它

定义随机变量 \(X\) ：代表所有可能与对应概率 $ (p_1,x_1),(p_2,x_2),... $
鞅 ： \(E[X_i|X_{i-1}] = X_{i-1}\) ，表示已知上一步随机变量，转移后的值相同
鞅更一般的定义：\(E[Y_i|X_{i-1}] = Y_{i-1}\)

• 例：
  对于抛硬币问题，令当下拥有的硬币为 \(X_i\) ，那么 \(X\) 为鞅
  令 \(Y_i\)=\(X_i^2-i\) ， 更具体地表示： \((p_1,x_1^2),(p_2,x_2^2),...\)，可证 \(Y\) 是关于 \(X\) 的鞅
  你会说这有什么用呢？：对于 \(X_n\) ，有 \(Y_n=X_n^2-n=Y_0=X_0^2-0\) , 当取开始值为 0 时，可大致反应抛硬币极限值和次数之间的关系

时停定理（其实叫停时定理）：
考略构造一个含有时间和状态信息的鞅

一篇博客

我真的浪费了2h学习一个我学了也不用不来的（对于我来说是）狗屎

7-18

原地爆炸

T1

回文数不多，预处理出来后无限背包

代码：数组开小

T2

1. 注意到题目条件限定一个汇点，发现每一个点对汇点产生的贡献就是路径数，然后特殊考虑一下两次汇入之间有空（比大小前要判是否取模）

2. 注意到 T=n 后，汇入之间不可能再有空，先暴力模拟前 n 次，再计算

代码：
遍历 DAG 时转移有循环，但是 deg[v]-- 也放在循环里了

T3

假设二分 limit ，变成处理城市之间的距离考虑是否连通 ， 这样就不用处理全部城市的距离 ，多源bfs 在交汇点上合并即可 于是我习惯性想到整体二分然后一去不复返
再考虑我们得到的性质：多元 bfs 只用做一次，可以得到所有城市之间最小的最大距离，建立最小生成树即可

代码：
1.内存开炸 *2
2.做 bfs 时不能直接建边，假设当前在扩展值为 d 的点，那么这个点当前可能和 d 或 d+1 的点连通，取到的不一定最优。存进数组里再排序 -> 代码尽量意义明白逻辑简单

T4

取max意味着很多子段不会做出贡献，所以考虑做出贡献的最简括号子序列，然后发现其形如 ((((...))))
具体地，对于一个序列，总能找到有且仅有一个划分点 x ，满足左边的左括号数和右边的右括号数相同
对于 ? 考虑枚举+构造使 x 成为贡献点并且可以直接算贡献
然后拆组合式，有 trick :

1. \(m(n,m)=n(n-1,m-1)\)，可以理解成从 a 个数中分两次选出一个数的总可能数（考虑赋予乘法组合意义）
2. \(\sum{(a,i)(b,c+i)} = (a+b,c)\) 组合意义较显然

ACM

然而不是 ac_machine

思想：同 kmp

利用字符串的连续性和枚举匹配时的重复信息，减少重复枚举
只关心是否匹配，所以只用考虑和匹配（文本串）相关的字符串

kmp : 一对一
遍历模式串时（模式串的前缀），同时记录可能匹配的后缀，其对应文本串的前缀
每一个匹配中的模式串子段都是文本串的前缀，所以只用在文本串上预处理即可
有一个链的关系：p -> kmp [ p ] 连向最长的可能后缀，是树

ACM : Trie 树上 kmp

1. 维护遍历模式串时（模式串的前缀）可能匹配的后缀
2. 模式串互相表示：用最长的覆盖其它 -> 不断走到最长的可能匹配前缀

所以有三种边

1. Trie 树边
2. 指向作为后缀被涵盖的其他前缀（也是可能匹配的其他前缀）
3. 无法匹配时转移到涵盖的可能前缀中最长的那个（大多数题目直接赋值给原空儿子即可）

两种转移：

1. 走 ：就是不断走向当前最长可能前缀
2. 跳 ：查询其他可能前缀

所以有一个链的关系：p -> kmp [ p ] 连向最长的可能后缀
所有 fail 是一棵根到子深度递增，fail边斜着长的树

代码：

1. 注意 'a' 和 'A'
2. 请调用 build()

7-19

T1

感觉很冗余，对于符合条件的一个字符串，考虑它的字串，发现全符合
枚举字符出现次数即可

T2

题目看错寄

对于 ( n , k ) = d ，会以 d 的间隔便利 n/d 个数每个遍历 d 遍
发现只与 d 有关，枚举因子即可
但我们注意到当前环，若其长度不为质数，那么这个环一定可以被表示成几个小环贡献的平均数，即一定有小环不劣于当前环，所以只用枚举质因子

代码：
为了省桶数组的内存，对每个 d 分别考虑 1~Q ，两个优先队列维护删除即可

才发现我复杂度错误全靠小常数优先队列碾过去（乐

T3

观察题目，易得倍增
也可以广义矩阵乘法，+ 和 max 可结合

代码：

while(K){
	if(K&1ll) sm=merge(sm,x);
	x=merge(x,x),K>>=1;
}

为了方便维护长度和转移，令状态 f [ u ] [ v ] 表示 [ u - > v )

T4

形如 kmp 所以考虑维护
由于字符串的性质，暴力枚举所有kmp并算贡献可以获得不错的分数，比如100
kmp 是一条在链上建立的树
对于当前点考虑继承上一点的贡献，那么要去除 x-1 到根节点上 所有 s [ k + 1 ] ! = s [ x ] 的 k 的贡献
删除操作显然只用 O(n) 次，尝试让找到每一个点的复杂度 O(1) 即可：对于 x 记录它的向上链第一个后继颜色为 k 的点
还要对所有值维护取 min 操作，最开始想的是利用不同值的单调性，但题解说只要把所有值存起来，每次删掉所有大于 v 的，再重新加到 c[v] 里，同样是利用删除复杂度只跟加入次数有关

代码：
map 的使用

auto it=c.upper_bound(x);
while(it!=c.end()){
	sm+=(*it).second,res-=1ll*(*it).first*(*it).second;
	it=c.erase(it);
}

二项式反演

7-20

T1

形如 \(x_1y_2>x_2y_1\) 可以转化成 \(x_1y_2-x_2y_1>0\) ，形如叉积，显然若 a x b , b x c > 0 ( a , b , c 都在第一象限)有 a x c >0
所以找性质再直接排序即可

T2

数据随机，深度期望 log
对每个节点维护两个子节点交换/不交换的值即可

代码：
pb_ds

T3

exgcd，显然

代码：
求 ax+by=c 时（我们已经保证 x , y 互质过了），先求 ax+by=1 的解，得出 ax+by=c 的通解，在去求特解

T4

因为最优策略，数据较小，图很难找性质，所以枚举所有选择对应的状态取最优
f [ s ] [ i ] [ j ] 表示占有魔法卷轴集合为 s ，当前先手在 i ，后手在 j 的最优值，转移显然
但是状态转移之间仍可能有环，考虑这种情况的 s 必然是不变的，所以我们对所有 s 相同的状态考虑它们之间的转移
先做 s' -> s 的情况，再对 DAG 跑
然后对于环的情况，令 g [ s ] [ i ] [ j ] 表示当前最优解，由于会新增贡献的结点最开始就跑了，所以每次取环上最大的 g [ s ] [ i ] [ j ] 更新其他点即可
但如果所有 g [ s ] [ i ] [ j ] 都 < 0，那么环不如在内部转移不走出去，所以环上点最小为 0 ，其他点最小 -inf

代码：
令 update ( s , i , j ) 处理 DAG 式的转移
用优先队列存储所有 g ( s , i , j )，掏出来时如果没有被 update 过就是环上的点。数据较小所以在 update 的时候就不断把更新过的点扔进去即可

决策单调性

“相交优于包含”
注意决策点单调不代表越接近决策点越优

1.栈维护决策点覆盖区间
2.(l,r,ql,qr) 处理决策点在 ( l , r ) 中的 ( ql , qr ）

7-21

T1

列朴素 DP 式子，发现可以把累加拆成前缀和相减，单调队列优化即可

做题：不同的状态都要尝试，取最方便的那个

T2

#include<bits/stdc++.h>
#define ll long long
#define mk make_pair
#define ph push_back
#define rep(i,l,r) for(int i(l),i##end(r);i<=i##end;++i)
#define per(i,r,l) for(int i(r),i##end(l);i>=i##end;--i)
using namespace std;
const int N=3e5+20;
struct bit{
	int n; ll c[N];
	bit(int n) :n(n) { rep(i,1,n) c[i]=0; }
	void ins(int x,ll v){
		if(x<0) return ;
		for(;x<=n;x+=x&-x) c[x]+=v;
	}
	ll qry(int x){
		if(x<=0) return 0;
		if(x>n) x=n;
		ll res=0; for(;x;x-=x&-x) res+=c[x]; return res;
	}
};
ll s1[N],s2[N];
struct solve{
	int n; bit a,b,c,d;//a,b倒序 
	solve(int n) :n(n),a(n),b(n),c(n),d(n) {}
	void ins(int x,ll v){
		a.ins(n-x+1,v),b.ins(n-x+1,v*x);
		c.ins(x,v*s2[x]),d.ins(x,v*s1[x]);
	}
	ll qry(ll x){
		return s2[x]*a.qry(n-x+1)+s1[x]*b.qry(n-x+1)+c.qry(x-1)+x*d.qry(x-1);
	}
};
struct CYD{
	solve &a,&b;//!
	ll as; int n,d[N];
	set<int> s;
	
	void add(int k){ a.ins(k,1),as+=b.qry(k); }
	void del(int k){ a.ins(k,-1),as-=b.qry(k); }
	
	CYD(int x[],int n,solve &a,solve &b) : a(a),b(b),as(),n(n){//有顺序要求 
		s.insert(1),s.insert(n+1);
		rep(i,2,n){
			d[i]=x[i]-x[i-1];
			if(!d[i])
				s.insert(i);
		}
		for(auto it=s.begin();next(it)!=s.end();++it)//!
			add(*next(it)-*it); 
	}
	
	void rw(int k,ll x){
		if(k==1||k==n+1||!x) return ;
		if(!d[k]){
			auto it=s.find(k),pre=prev(it),nxt=next(it);//!
//			printf("0 %d %d %d\n",*it,*pre,*nxt);
			del(*it-*pre),del(*nxt-*it);
			add(*nxt-*pre);
			s.erase(k);
		}else if(d[k]+x==0){
			auto it=s.insert(k).first,pre=prev(it),nxt=next(it);//!
//			printf("1 %d %d %d\n",*it,*pre,*nxt);
			add(*it-*pre),add(*nxt-*it);
			del(*nxt-*pre);
		}
		d[k]+=x;
	}
};
int a[N],b[N];
signed main(){
	freopen("garden.in","r",stdin);
	freopen("garden.out","w",stdout);
	int n,m,Q,op,l,r,x;
	scanf("%d%d%d",&n,&m,&Q);
	
	rep(i,1,max(n,m)) s1[i]=s1[i-1]+i,s2[i]=s2[i-1]+1ll*i*i;
	rep(i,1,max(n,m)) s2[i]-=1ll*i*s1[i];
	
	rep(i,1,n) scanf("%d",&a[i]);
	rep(i,1,m) scanf("%d",&b[i]);
	
	solve sa(n),sb(m);
	
	CYD wka(a,n,sa,sb),wkb(b,m,sb,sa);
	
	printf("%lld\n",wkb.as);
	while(Q--){
		scanf("%d%d%d%d",&op,&l,&r,&x);
		if(op==1) wka.rw(l,x),wka.rw(r+1,-x);
		else wkb.rw(l,x),wkb.rw(r+1,-x);
		printf("%lld\n",wka.as+wkb.as);
	}
	return 0;
}

T3

#include<bits/stdc++.h>
#define ll long long
#define mk make_pair
#define ph push_back
#define rep(i,l,r) for(int i(l),i##end(r);i<=i##end;++i)
#define per(i,r,l) for(int i(r),i##end(l);i>=i##end;--i)
using namespace std;
const int N=5e5+20;
int ns,rt[N];
struct node{ int l,r,c; }tr[N*17];
#define lc tr[p].l
#define rc tr[p].r
#define mid (l+r>>1)
void build(int &p,int l,int r){
	p=++ns;
	if(l==r){ tr[p].c=1; return ; }
	build(lc,l,mid),build(rc,mid+1,r);
	tr[p].c=tr[lc].c+tr[rc].c;
}
bool chk(int p,int l,int r,int x,int y){
//	printf("%d %d   %d %d   %d\n",l,r,x,y,tr[p].c);
	if(!tr[p].c||x>y||x>r||l>y) return 0;
	if(x<=l&&r<=y) return tr[p].c>0;
	return chk(lc,l,mid,x,y)||chk(rc,mid+1,r,x,y);
}
void copy(int p,int &q,int l,int r,int x,int y){
	if(!p) return ;
	if(x<=l&&r<=y){ q=p; return ; }
	if(!q) q=++ns;
	if(x<=mid) copy(lc,tr[q].l,l,mid,x,y);
	if(y>mid) copy(rc,tr[q].r,l,mid,x,y);
	tr[q].c=tr[lc].c+tr[rc].c; 
//	printf("%d %d   %d %d   %d %d\n",l,r,x,y,tr[p].c,tr[q].c);
}
#undef mid
signed main(){
	freopen("grow.in","r",stdin);
	freopen("grow.out","w",stdout);
	int n,Q,op,x,y,v;
	scanf("%d%d",&n,&Q);
	build(rt[0],1,n);
	while(Q--){
		scanf("%d%d%d",&op,&x,&y);
		if(op==1){
			scanf("%d",&v);
			copy(rt[v],rt[v+1],1,n,x,y);
		}else{
			int l=1,r=n,mid,as=0;
			while(l<=r){
				mid=(l+r)>>1;
				if(chk(rt[mid],1,n,x,y)) as=mid,l=mid+1;
				else r=mid-1;
			}printf("%d\n",as);
		}	
//		rep(i,0,n) printf("%d ",rt[i]); puts("");
	}
	return 0;
}

7-22

T1

区间转化成端点前缀和相“减”
然后再桶数组维护

T2

思路：

1. 直接考虑，令 f [ i ] 表示由 i 构造的在 1 ~ i-1 内没出现过的个数，根据性质转移
2. 考虑转化，对于每两个 1 之间，可以认为其中有 长度>=0 的 0区段，记为 a
   两种操作 1.(a>0) a-1 相当于去掉一个0 2.(a=0) 删掉a 相当于把两边的1合并
   那么处理时就很简单不用考虑操作带来的影响

代码：

1. 把两端的 0 去了最后再处理影响：特殊处理特别状态减小代码复杂度！
   代码复杂度：不是指码量，而是其直观度&不容易错的程度
2. debug时针对状态转移各种情况都要考虑！

T3

T4

凸包 - 分块

7-28

Splay

void rotate(int x){//一般来说，Splay的节点是已经遍历下去的，不需要pushdown
	if(x==rt) return ;
	int y=fa[x],z=fa[y];
	int d=ch[y][1]==x;
	if(y==rt) rt=x,fa[x]=0;//fa[rt]=0!!!
	else ch[z][ch[z][1]==y]=x,fa[x]=z;
	ch[y][d]=ch[x][d^1],fa[ch[x][d^1]]=y;
	ch[x][d^1]=y,fa[y]=x;
	pushup(y),pushup(x);//!!!
}
void splay(int x,int goal){//为方便分出子树进行操作，设置终止节点
	while(fa[x]!=goal){//x取不到goal
		int y=fa[x],z=fa[y];
		if(fa[y]!=goal){
			if((ch[y][0]==x)^(ch[z][0]==y)) rotate(x);
			else rotate(y);	
		}
		rotate(x);
	}
}

时间复杂度见势能分析，严格 \(logN\)