图解：如何理解与实现散列表

散列表（Hash table），也叫做哈希表，是根据键（Key）而直接访问在内存存储位置的数据结构。也就是说，它通过计算一个关于键值的函数，将所需查询的数据映射到表中一个位置来访问记录，它充分利用了数组支持按照下标随机访问元素的特性这加快了查找速度。这个映射函数称做散列函数，存放记录的数组称做散列表。

散列表的概念

散列表是算法在时间和空间上做出权衡的经典例子。如果没有内存的限制，我们可以直接将键作为数组的索引（可能超级大），那么所有的查找操作只需要访问内存一次即可完成。另一方面，如果没有时间的限制，我们可以使用无序数组并进行顺序查找，这时只需要很小的内存但是耗时严重。而散列表则是在这两者之间找到了一种平衡。

散列函数

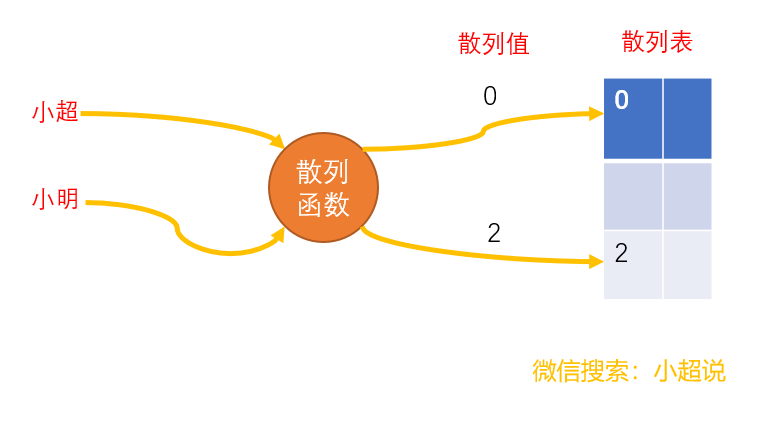
散列函数，顾名思义，它是一个函数。我们把它定义成 hash(key) ，其中 key 表示元素的键值，则 hash(key) 的值表示经过散列函数计算得到的散列值。它的任务就是将键转化为数组的索引。

该如何构造散列函数呢？
基本要求：

• 1.散列函数计算得到的散列值是一个非负整数
• 2.如果 key1 = key2，那 hash(key1) == hash(key2)；
• 3.如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)。

更进一步，一个优秀的散列函数需要满足

• 一致性————等价的键必然产生相等的散列值
• 高效性————计算简洁
• 均匀性————均匀地散列所有的键

一些著名的哈希算法(如MD5,SHA,CRC等)

MD5消息摘要算法（MD5 Message-Digest Algorithm），一种被广泛使用的密码散列函数，可以产生出一个128位（16字节）的散列值（hash value），用于确保信息传输完整一致。将数据（如一段文字）运算变为另一固定长度值，是散列算法的基础原理。

安全散列算法（英语：Secure Hash Algorithm，缩写为SHA）是一个密码散列函数家族，是FIPS所认证的安全散列算法。能计算出一个数字消息所对应到的，长度固定的字符串（又称消息摘要）的算法。且若输入的消息不同，它们对应到不同字符串的几率很高。

循环冗余校验（英语：Cyclic redundancy check，通称“CRC”）是一种根据网络数据包或电脑文件等数据产生简短固定位数校验码的一种散列函数，主要用来检测或校验数据传输或者保存后可能出现的错误。生成的数字在传输或者存储之前计算出来并且附加到数据后面，然后接收方进行检验确定数据是否发生变化。

不过，无论这个散列函数有多好，我们总不能避免散列冲突。也就是第三条

如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)

不能始终被满足。

我们直观上可以感受得到，散列函数仅仅为我们提供了一种对应关系。如果需要确切的证明，我们可以考虑数学上的抽屉原理：假设散列函数产生的散列值总数是N,我们的键有N+1个，那么，必然存在两个键对应的散列值相同！直观来讲，键越多，发生散列冲突的概率就越大！

针对散列冲突，我们下文介绍两种常见的处理方法：开放寻址法和链表法。

开放寻址法

实现散列表的一种方法是用大小为M的数组保存N个键值对，其中M>N，我们需要依靠数组中的空位来解决碰撞冲突。基于这种策略的所有方法统称为开放寻址法。我们下文介绍开放寻址法最简单的方法：线性探测法。

当我们往散列表中插入数据时，如果某个数据经过散列函数散列之后，存储位置已经被占用了，我们就从当前位置开始，依次往后查找，看是否有空闲位置，如果到了尾部，还是没有找到空闲位置，那么就再从头开始找，直到找到空闲位置。

查找的时候可能会产生以下三种结果：

• 命中，该位置的键和被查找的键相同
• 未命中，键为空（该位置没有键）
• 继续查找，该位置的键和被查找的键不同。

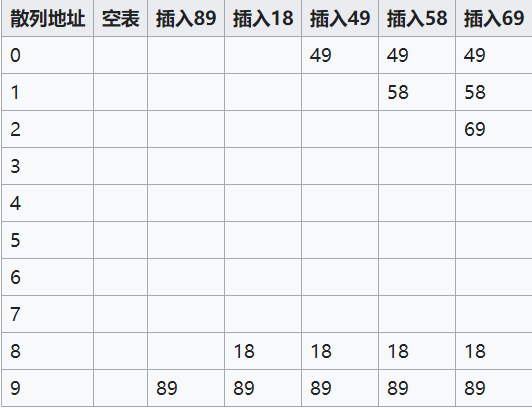
我们来看一个例子：将键为{89,18,49,58,69}插入到一个散列表中的情况。假定散列函数法则为：取键除以10的余数作为散列值。

第一次冲突发生在填装49的时候。地址为9的单元已经填装了89这个关键字，所以继续向后查找空位置，发现下一位为空，所以将49填装在地址为0的空单元。第二次冲突则发生在58上，往下查找3个单位，将58填装在地址为1的空单元。69同理。

对于使用线性探测法解决冲突的散列表，删除操作稍微有些特别。我们不能单纯地把要删除的元素设置为空。这是因为在查找的时候，一旦我们找到一个空闲位置，我们就认定散列表中不存在这个数据。但是，如果这个空闲位置是我们后来删除的，就会导致原来的查找算法失效。本来存在的数据，会被认定为不存在。

那么这个问题如何解决呢？我们可以将删除的元素，特殊标记为 deleted。当线性探测查找的时候，遇到标记为 deleted 的空间，并不是停下来，而是继续往下探测。

不管采用哪种探测方法，当散列表中空闲位置不多的时候，散列冲突的概率就会大大提高。

为了尽可能保证散列表的操作效率，一般情况下，我们会尽可能保证散列表中有一定比例的空闲槽位。我们用装载因子（load factor）来表示空位的多少。装载因子的计算公式为：
散列表的装载因子=填入表中的元素个数/散列表的长度

装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降。因此我们需要动态地调整数组的大小保证装载因子不会超出某个临界值。

链表法

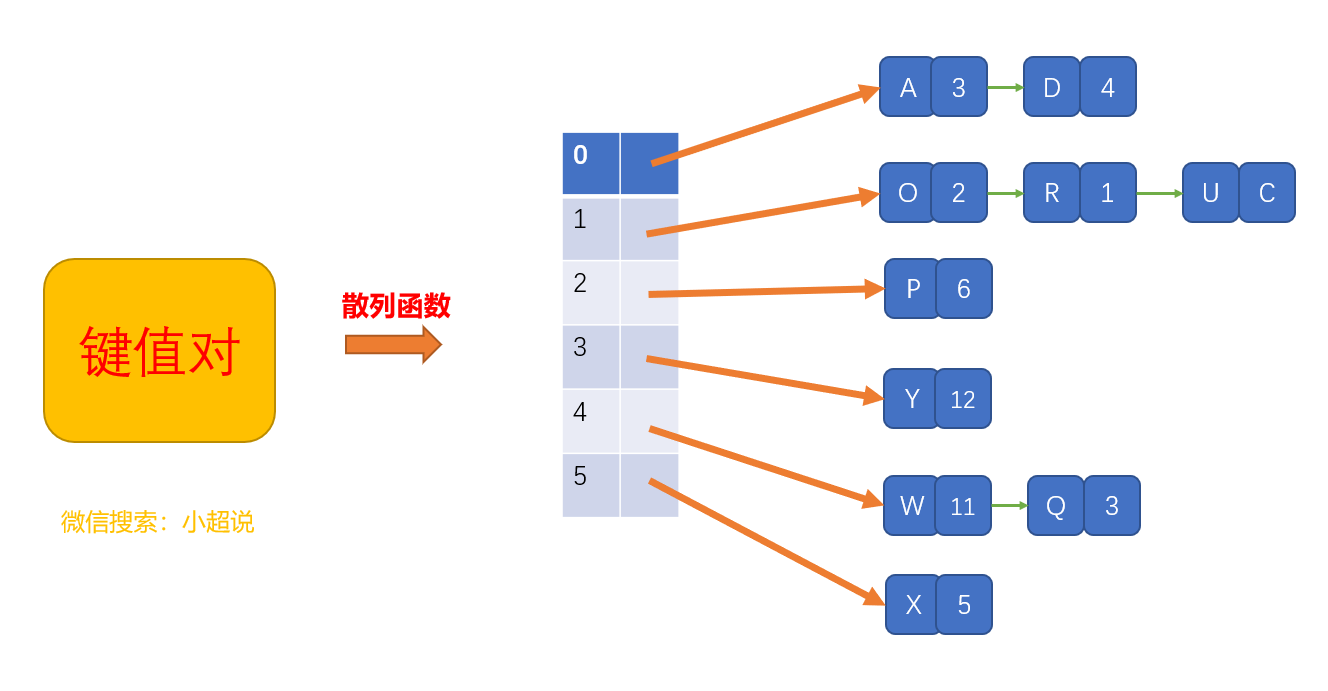
链表法是一种更加常用的散列冲突解决办法，相比开放寻址法，它要简单很多。如下图所示，在散列表中，每个位置对应一条链表，所有散列值相同的元素都放到相同位置对应的链表中。

查找分两步：首先根据散列值找到对应的链表，然后沿着链表顺序查找相应的键

当插入的时候，我们只需要通过散列函数计算出对应的散列槽位，将其插入到对应链表中即可，所以插入的时间复杂度是 O(1)。

当查找、删除一个元素时，我们同样通过散列函数计算出对应的槽，然后遍历链表查找或者删除。时间复杂度跟链表的长度 k 成正比，也就是O(k)。对于散列比较均匀的散列函数来说，理论上讲，k=n/m，其中 n 表示散列中数据的个数，m 表示散列表中“槽”的个数。

“秒传”的背后

文件的哈希值也被称为“数组签名”，我们可以通过判断两个文件的哈希值是否相同来判断两个文件是否相同

首先给出一个事实：网盘上存储了大量相同的文件。那么既然是一样的文件，我就可以在后台只存一份，然后在用户的前端显示每个人都有一份。当某些用户要删除这个文件的时候，我并不真的删除，只需要在前端显示已经删除了，但后端一直保留着以供其他拥有此文件的用户下载。直到所有使用此文件的用户都删除了这个文件我再真的将其删除。

同理，在用户上传文件时，首先判断待上传文件的哈希值，一旦计算出用户要上传的数据和服务器上已经存储的某个数据是一样的，就不用上传了，直接在用户那里标记上这个文件已经上传成功了。这个过程几乎是瞬间搞定了，所以就成功实现了“秒传”！

全文完