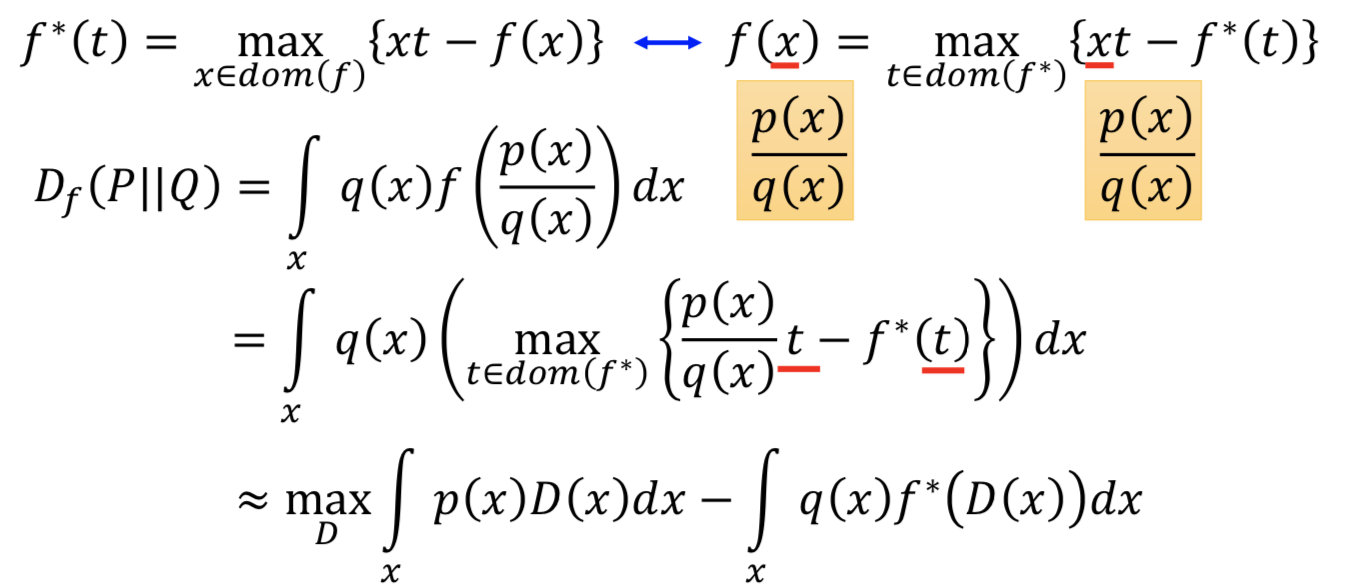任务:想要找到一个高维空间中的分布 P_data(x),要在目标类别的区域,采样的概率是高的;在那个区域之外,probability是低的。但这个P_data(x)分布的具体形式(pdf)是不知道的,GAN 就是要找到这个数据分布。
没有 GAN 怎么做生成?—— 极大似然估计
1. 从 P_data(x) 中 sample 一些数据作为训练数据
2. 借助一个含有未知参数 θ 的分布P_G(x; θ),想做的事情就是找出能够让 P_G 和 P_data 最接近的参数 θ。比如我们有一个混合高斯分布 GMM 作为P_G(x; θ),θ 就是 Gaussians 的一组 means 和 variances。
3. 由训练数据 {x1, x2, ..., xm} 和假设的含参分布的 pdf 来计算 P_G(xi; θ)
4. likelihood就定义为 ∏ P_G(xi; θ) ,一般会取对数
5. 就用 gradient ascent 或者其他优化方法让这个 likelihood 最大

接下来,先放结论: maximum likelihood estimation 就等价于 minimize KL Divergence
把上面的对数似然函数写成积分形式可能看的清楚点,因为是要对 θ 取 argmax,所以在后面加上一个 θ 无关的项,不影响 argmax 计算。明显可以看出积分号里面是 P_data * log(P_G / P_data),能够得出结论:对 P_G 的最大似然估计,等价于最小化 P_data 和 P_G 的KL散度。
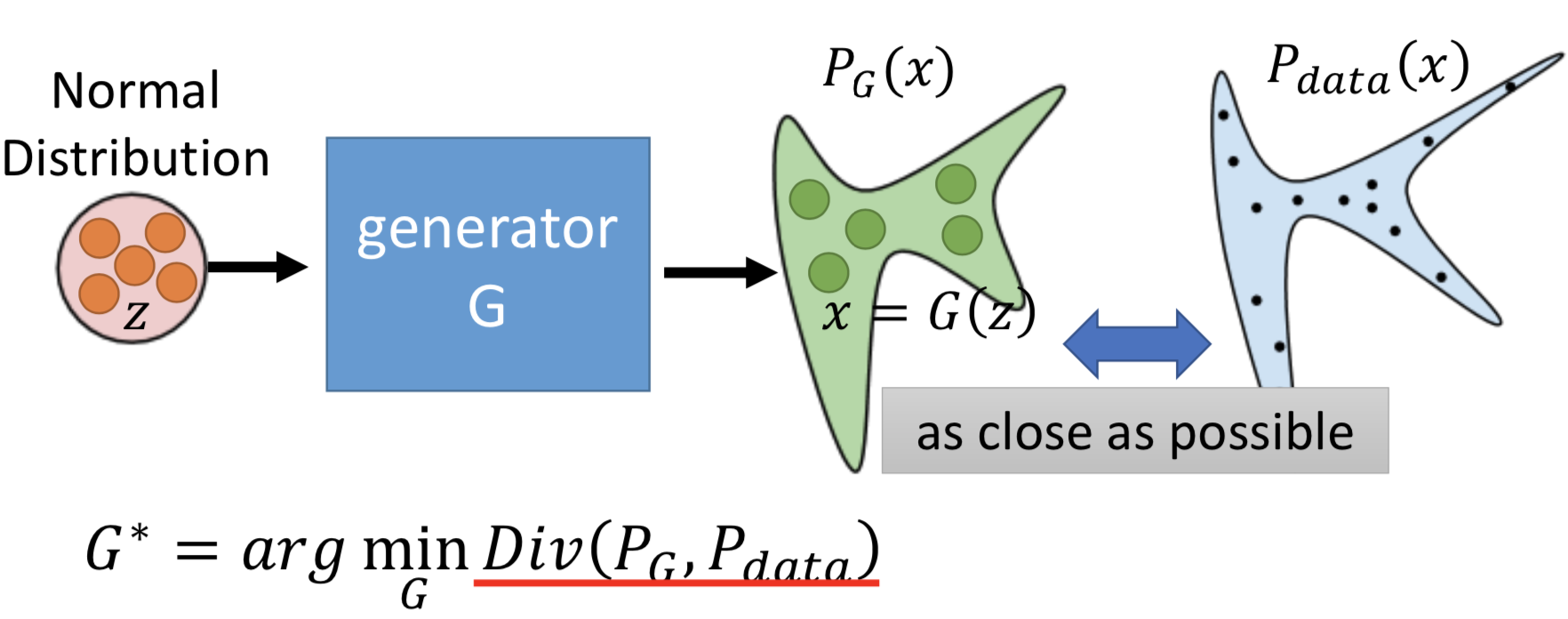
那问题就来了,怎么才能定义一个 general 的 P_G 呢?(因为如果很复杂、而且不知道 pdf 的明确的形式的话,对数似然函数没法计算)
定义一个 generator 作为生成 P_G 的方式(NN 隐式定义复杂概率分布的 pdf)。从一个很简单的先验(而且这个简单的先验分布具体是高斯还是别的,影响不大),映射成一个复杂的分布。
但是没法直接做,因为 P_G 和 P_data 的 pdf 的具体形式都是不知道的,就没法直接计算 divergence 然后 argmin。这个就是 GAN 解决的关键点。
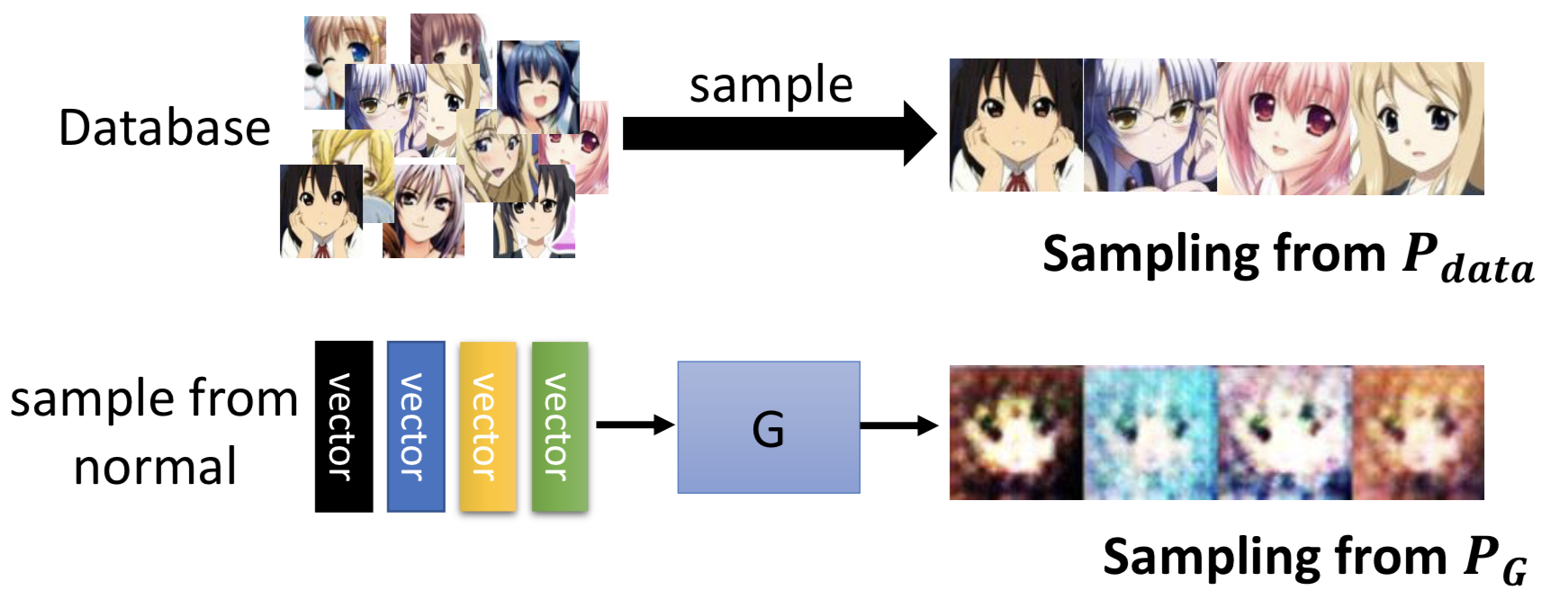
虽然不知道 P_G 和 P_data 的定义式,但是我们可以从这两个分布中 sample 数据出来(借助 NN 的拓扑结构):收集训练数据,就是从 P_G 分布 sample ;从先验分布 sample 然后经过 generator 得到G(z),就是从 P_data 分布 sample。
然后问题就剩下怎么计算这两个分布的 divergence ?—— 通过 discriminator。
也就是说,训练 discriminator :D* = argmax V(G, D) (仔细看看目标函数,这其实就是去训练一个 binary classifier 而已)
为什么这样就能最小化 P_G 和 P_data 的之间 divergence ?
先固定 G ,想要通过 D 来最大化 V(G, D)
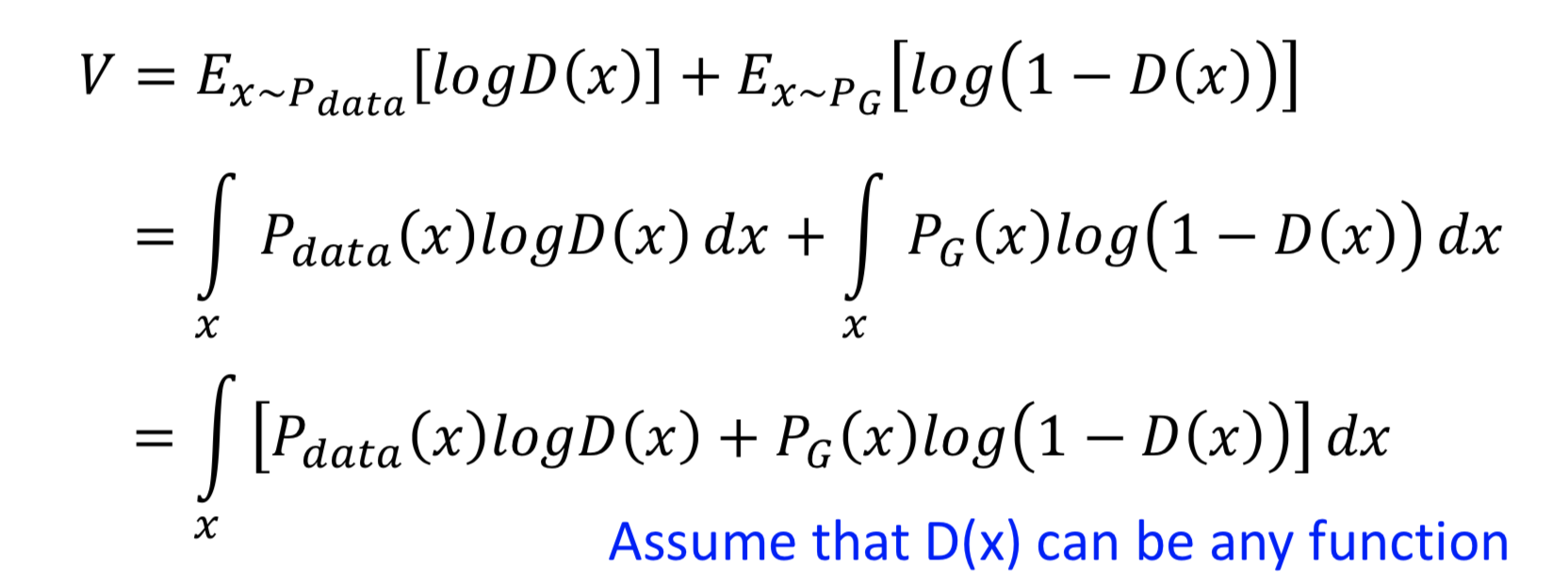
重要假设是,D(x) 可以是任意函数(NN拟合的理想情况),那么对于某一个 x ,都可以找一个 D(x) 令 V(G, D) 最大。V 对 D 求梯度后令其为0,得到极大值点 D(x) = P_data(x) / ( P_data(x) + P_G(x) )

再把 D* 代入 V(G, D) 中,就得到了 maxD V(G, D) = V(G, D*) 。然后把log里面的分母除以2,就能提出来两个 -log2

提出来常数项 -2log2 之后,可以发现后面剩下的部分就是两倍的JS散度。因为 JS散度定义为 JSD(P || Q) = KL(P || M) /2 = KL(Q || M) /2,其中 M = (P + Q) / 2
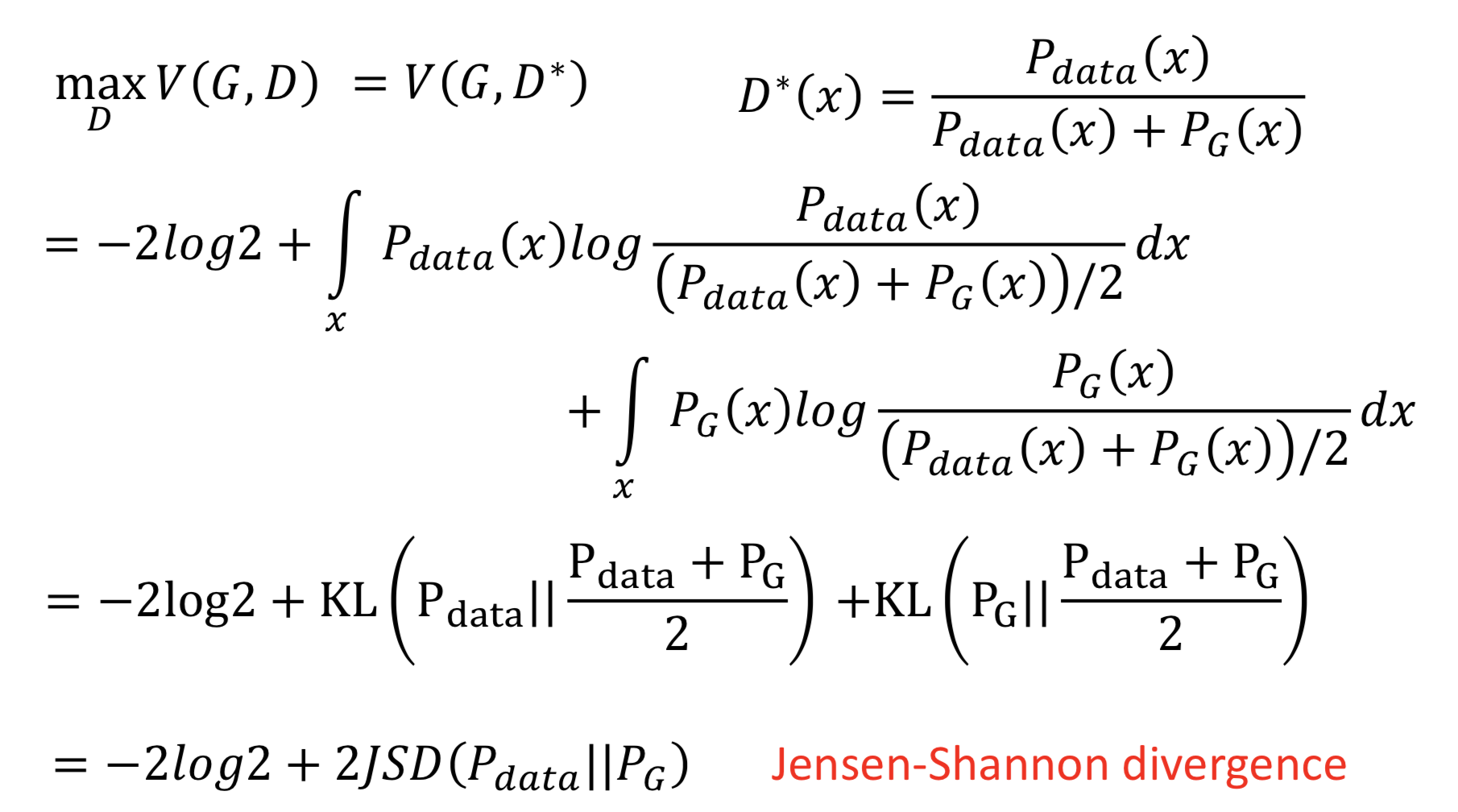
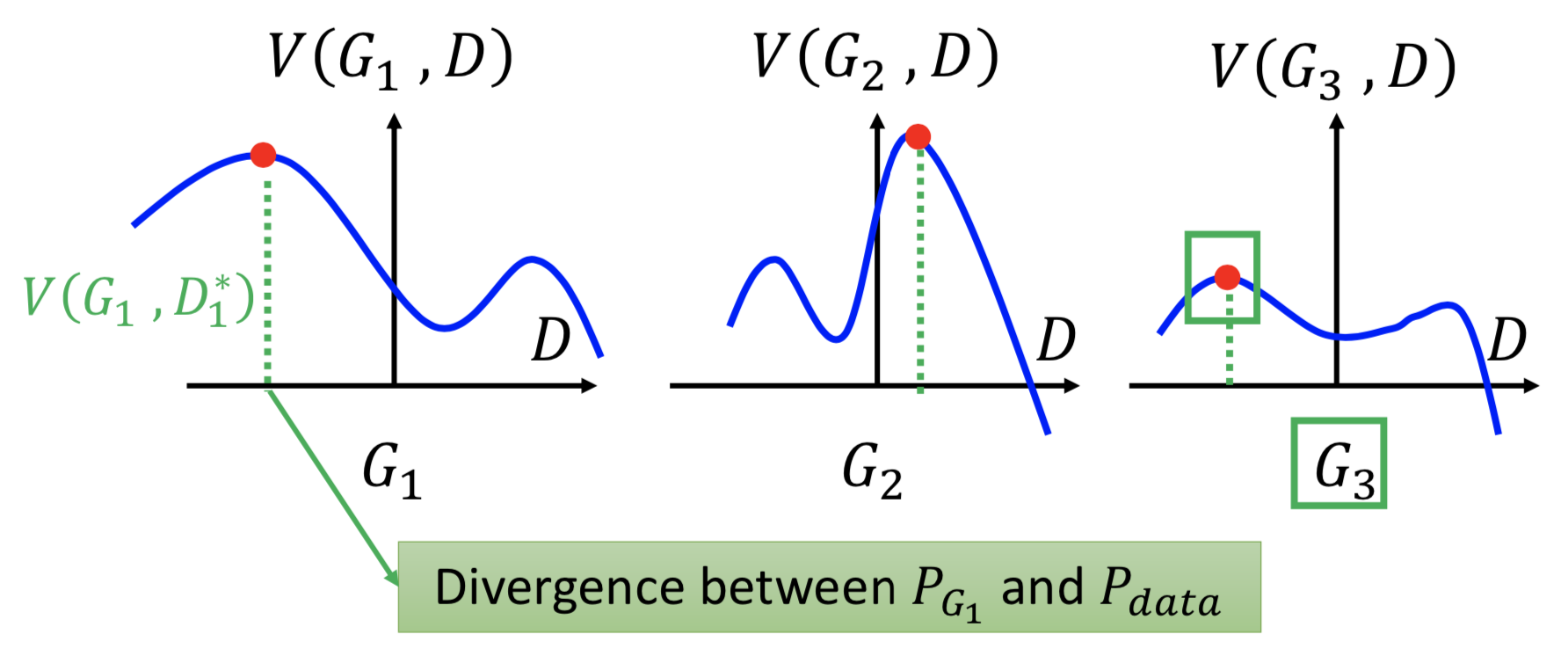
到这里就比较清楚了,接下来就要找一个 G ,最小化 JSD(P_data || P_G) 。举个例子,假设只有3个 G 可以选,那么先对每个固定的 G 找 V(G, D*),然后找一个 Gi 令 V(Gi, D*) 最小,下图所示显然应该选 G3。
对应 GAN 的训练过程,总结一下:

对于 G 的训练,就是要在固定刚才找到的最好的 D 之后,最小化 L(G, D)
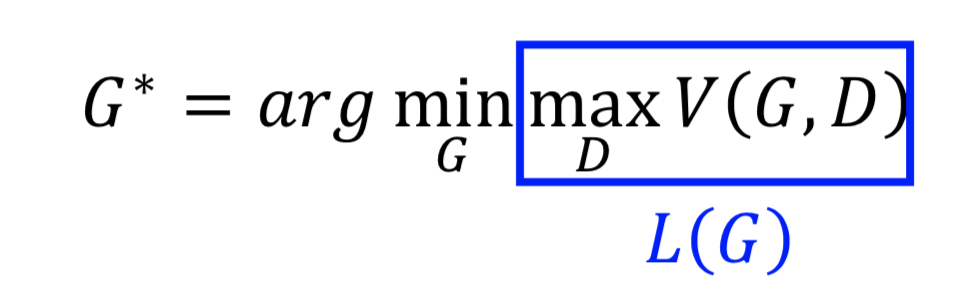

这里有个疑问,L(G) 中有 max 函数,能够求梯度吗? —— 可以,分段求(回忆一下 maxout network)

还存在别的问题吗?
更新 G 那一步,会改变 V(例如下图固定 D0*,但更新G0 -> G1 可能导致 V(G, D0*) 变成另一个不同的函数,那么 D0* 就已经不是令 V(G, D) 最大的 D 了)。从 V(Gt, Dt*) 到 V(Gt+1, Dt*),而这个时候 L(G)可能已经不再是 V(Gt+1, Dt*),而是 V(Gt+1, Dt+1*)。 Dt* 不一定等于 Dt+1*,所以做法就是假设这两个值是近似的。
不要一次更新 G 太多,而应该尽量要把 D 训练到底,至少要找到一个local maxima。
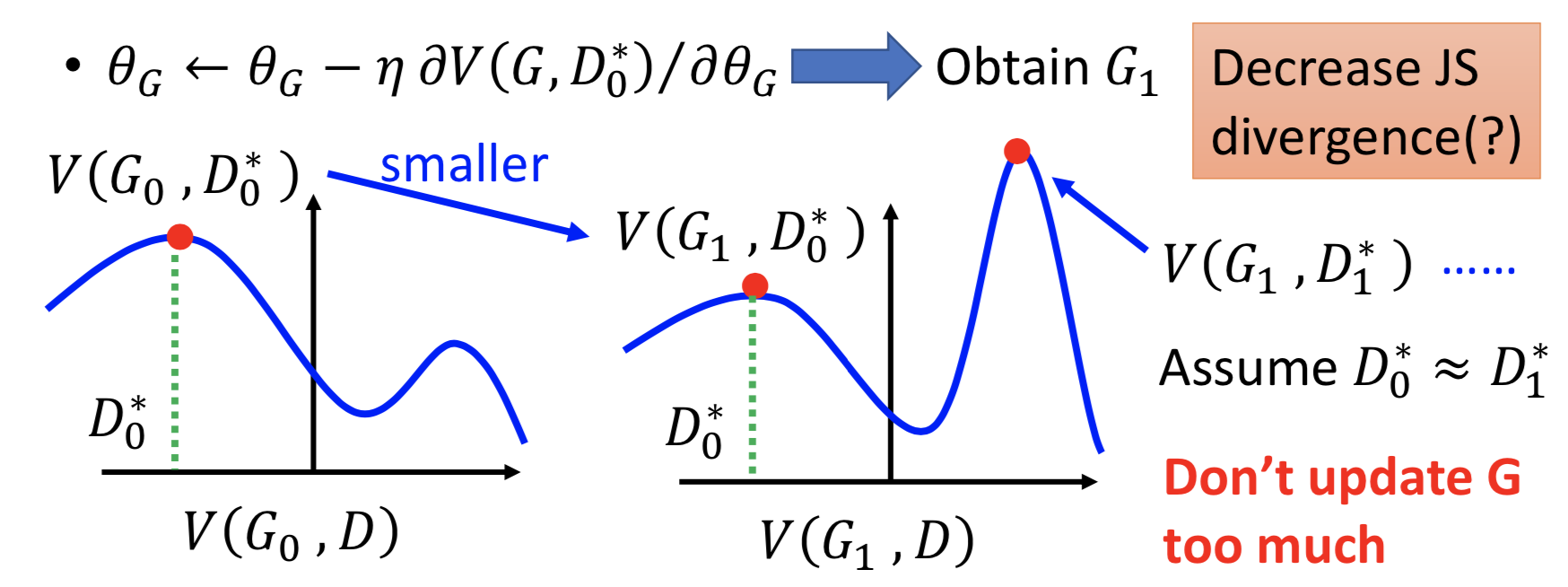
回顾一下整个 GAN 的训练流程和实际做法:

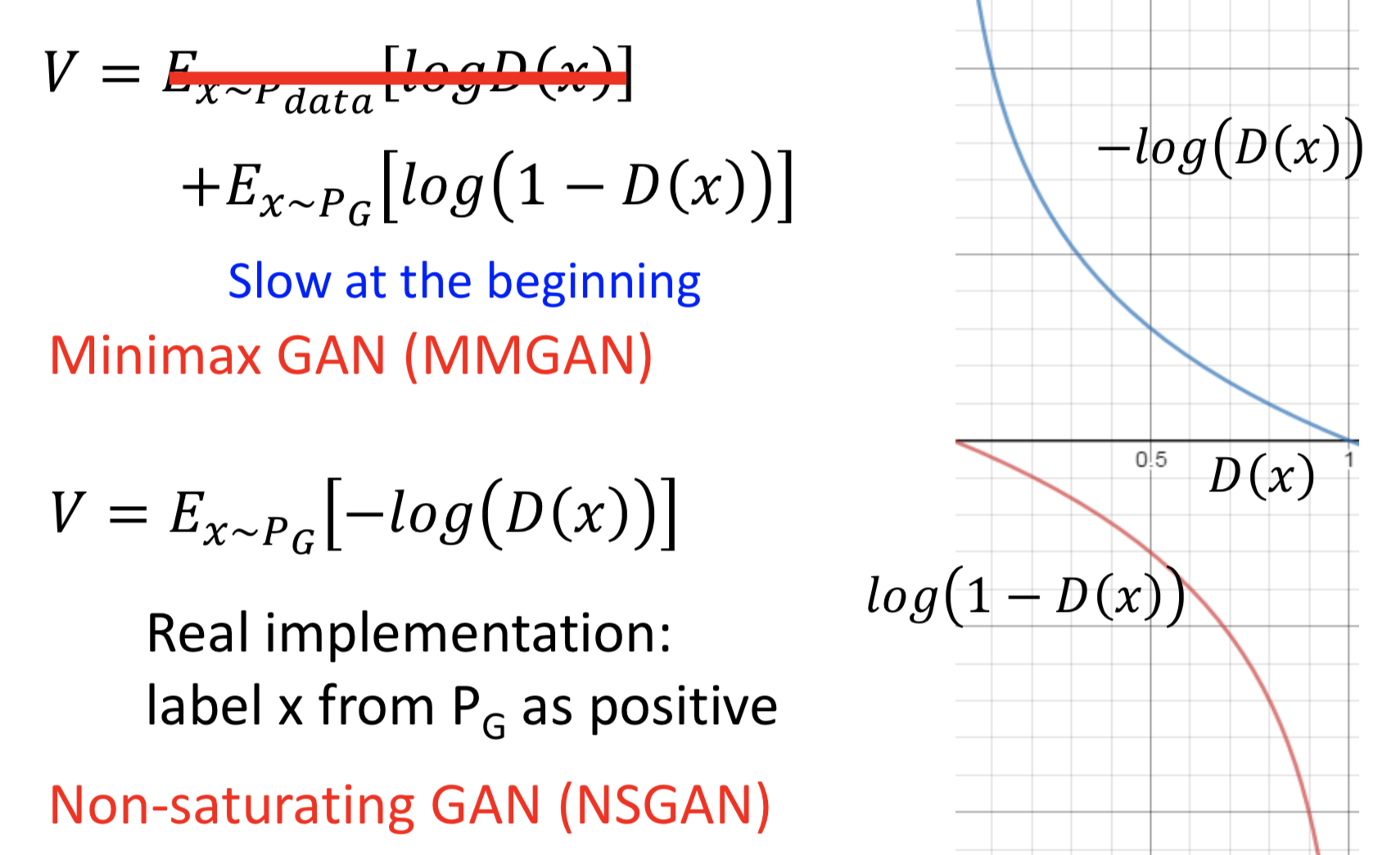
这里面还有个技巧,实际上训练 G 的目标函数可以不跟上面的公式一模一样,因为原来的式子会导致起始的时候梯度很小、更新的会很慢
实际的训练过程中,真的会导致 D 最后训练得如下图所示吗(完全不能做判别)?
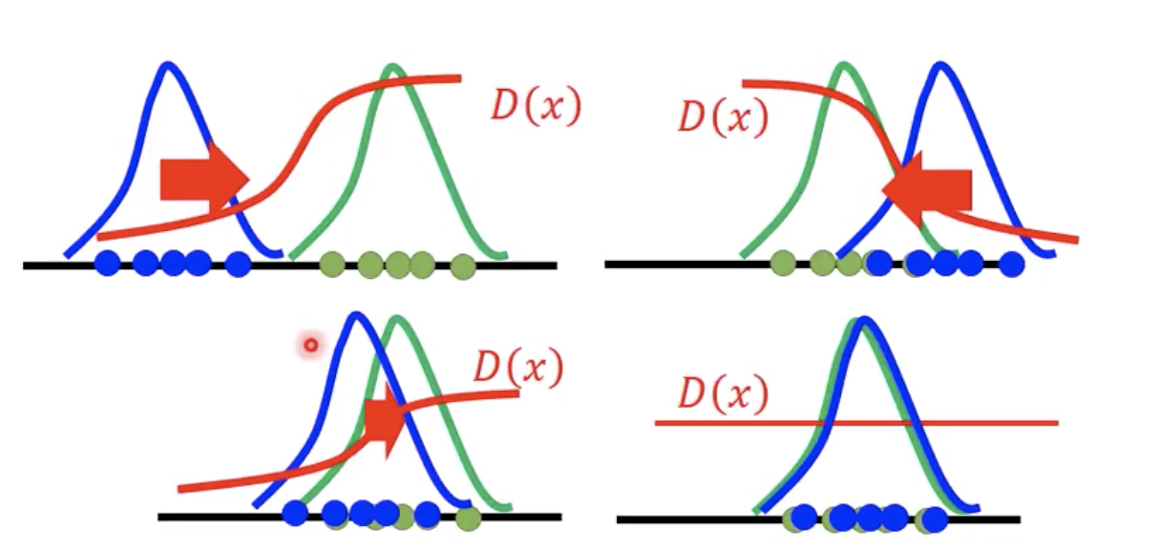
我自己觉得不会。。。因为实际的训练不会这么理想,本身就有太多假设和近似在里面。
GAN 的一般框架:fGAN
如何把不同的 f-divergence 应用到 GAN 中。 f-divergence 的定义:
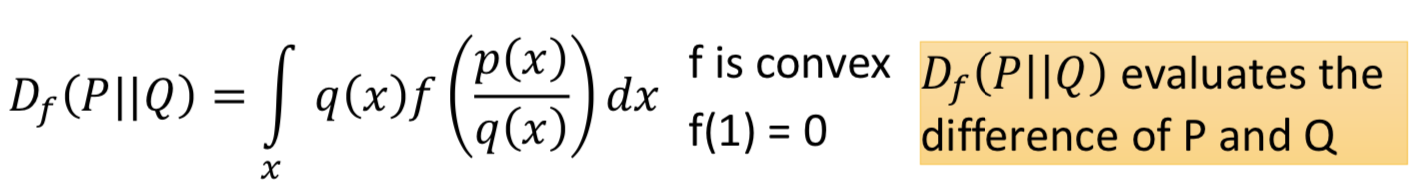
满足一些性质:当 p(x) = q(x),Df (P || Q) = 0;并且 Df (P || Q) >= 0

一些常见的 f-divergence 和对应的 f 函数:

任意一个凸函数 f 都有一个共轭函数 f*,满足
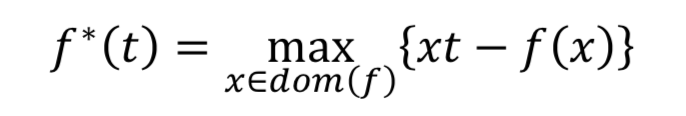
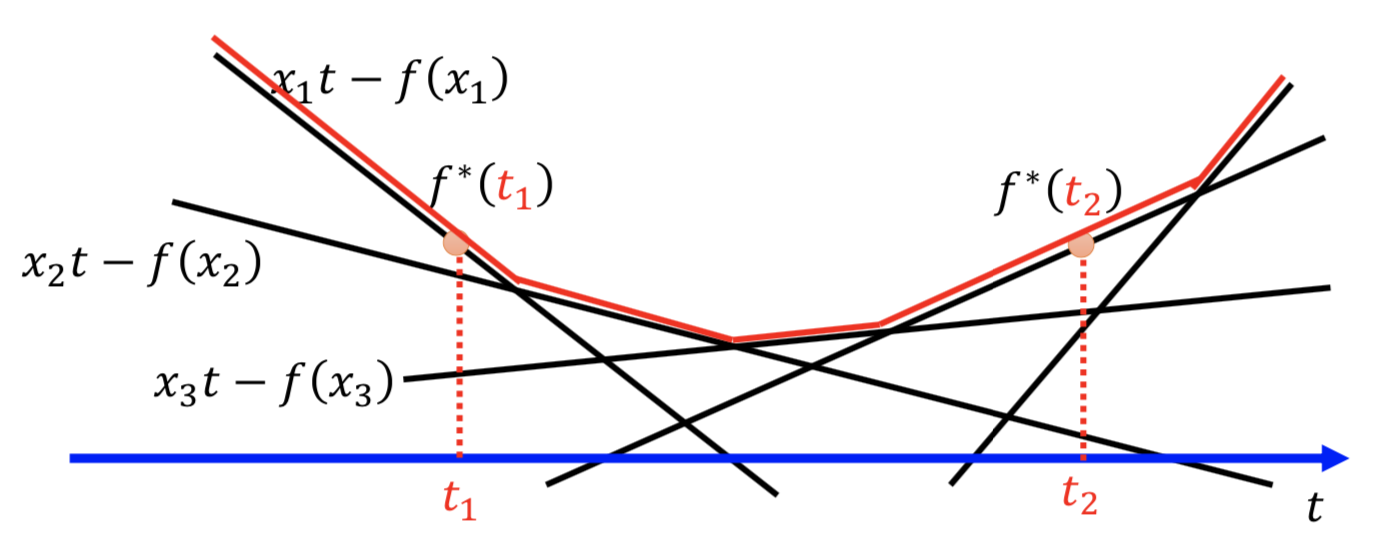
求解方式如下图所示,穷举所有的 x,所有的直线 xt-f(x) 求包络线就行了
回到 Df (P || Q) 的表达式,f 的自变量是 p(x) /q(x),代入。本来要穷举所有的 t 让后面的项最大,现在就找一个 D(更新 D 的参数),令 D(x) = t 使得后面的项最大。
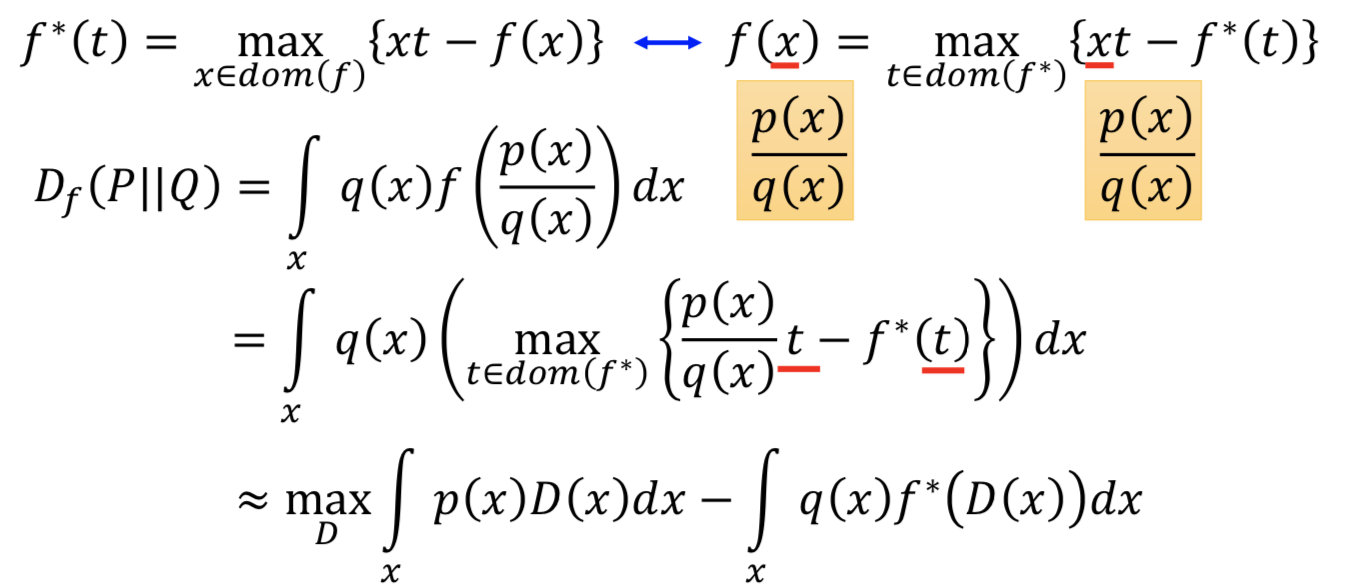
其中,由于 D 的拟合能力有限,所以只能得到一个下界

所以,把积分写成对分布求期望

这就是把不同的 f-divergence 应用到 GAN 中的目标函数了

这样做是要解决什么问题? —— Mode Collapse、Mode Dropping
生成数据的模式太集中
Mode Collapse:

Mode Dropping:

这可能是散度的选择导致的,所以就多一些可能的 f-divergence 来选择,然后 ensemble 一下。(不过其实已经有更好的解决方案了)


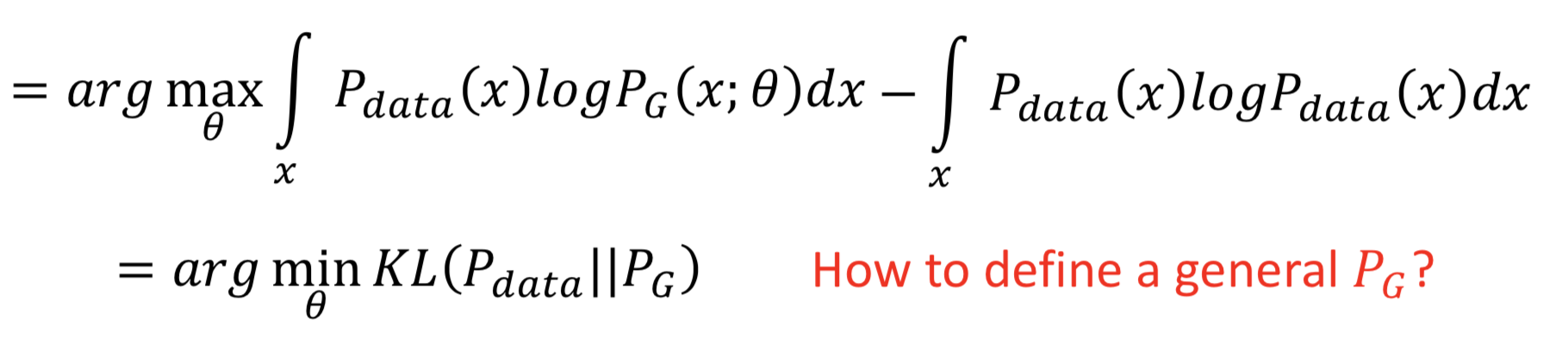

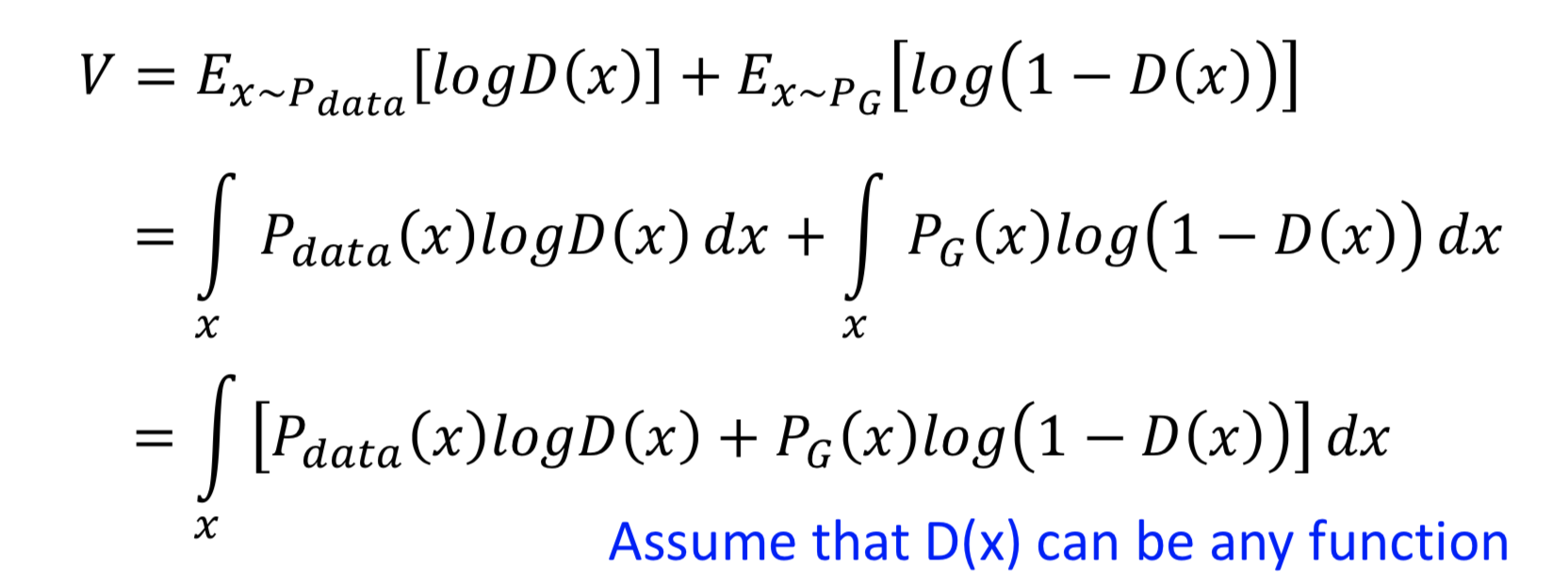


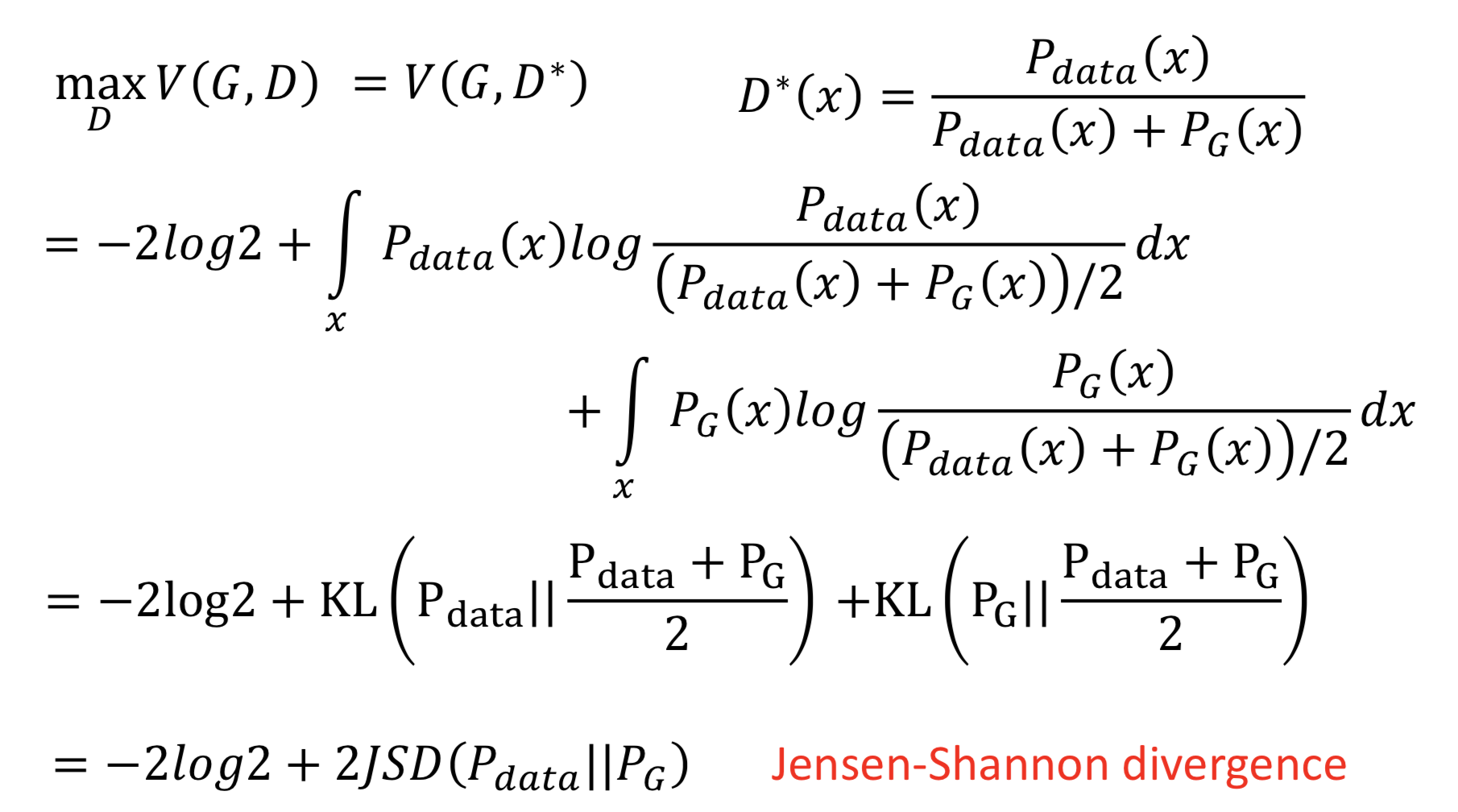


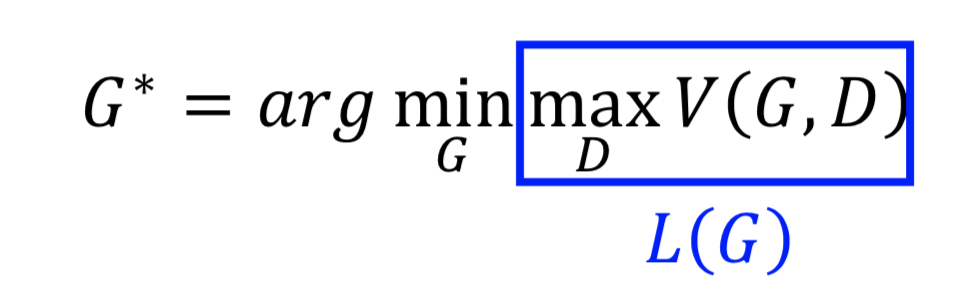






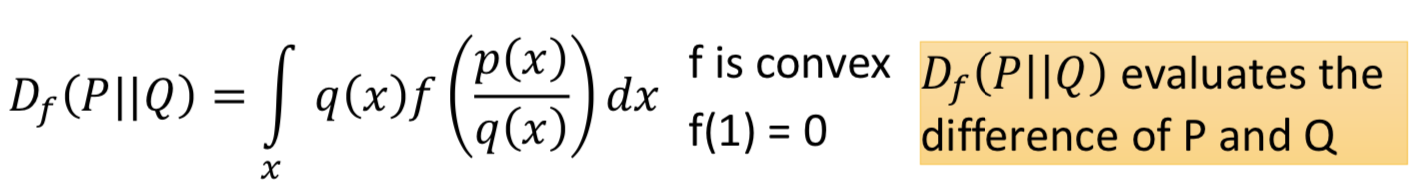


![]()