Leetcode-动态规划
70. 爬楼梯 https://leetcode-cn.com/problems/climbing-stairs/
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
解:
暴力,如果只有一阶,就只有一种方法;如果只有二阶,就只有两种方法。那么n阶的方法数就等于n-1阶和n-2阶方法数之和。但直接递归,有太多重复计算,超时。O(2n)
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 2:
return n
return self.climbStairs(n-1) + self.climbStairs(n-2)
递归+记忆化,放数组里缓存。把每一步的结果存储在 memo 数组之中,每当函数再次被调用,就直接从 memo 数组返回结果
class Solution:
def climbStairs(self, n: int) -> int:
memo = [0]*(n+1) # memo[i]表示从第i阶到第n阶的方法数,出发点是第0阶
def helper(i, n, memo): # 起始点i,终点n
if i > n: # 越界,最高起点直接在第n阶
return 0
if i == n: # 不用动,就这一种方法
return 1
if memo[i] > 0:
return memo[i] # 如果已经算过了,就不用再算了
memo[i] = helper(i+1, n, memo) + helper(i+2, n, memo)
return memo[i]
return helper(0, n, memo)
动态规划,递推, f(n) = f(n-1) + f(n-2) ,f(1)=1 , f(2)=2。O(N) 其实也可以不用开一个数组。
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 2:
return n
f = [0]*n
f[0], f[1] = 1, 2
for i in range(2, n):
f[i] = f[i-1]+ f[i-2]
return f[n-1]
# O(1) 空间
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 2:
return n
pre1 = 1
pre2 = 2
for i in range(2, n):
cur = pre1 + pre2
pre1 = pre2
pre2 = cur
return cur
特征根,特征方程为 a2 - a - 1 = 0

import math
class Solution:
def climbStairs(self, n: int) -> int:
sqrt5 = math.sqrt(5)
res = math.pow((1+sqrt5)/2, n+1) - math.pow((1-sqrt5)/2, n+1)
return int(res/sqrt5)
Binets 矩阵乘法,O(logN)。
[fn, fn-1] = [[1, 1], [1, 0]]*[fn-1, fn-2] = Q*[fn-1, fn-2] = Qn-2[f2, f1]
120.三角形最小路径和 https://leetcode-cn.com/problems/triangle/
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
说明:
如果你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题,那么你的算法会很加分。
解:
显然简单的贪心是不行的。
dfs,自顶向下,O(2n),显然很可能超时。
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
self.res = float('inf')
n = len(triangle)
def dfs(level, col, pre_sum): # 搜索到位置(level,col),之前路径和为pre_sum
cur_sum = pre_sum + triangle[level][col]
if level == n-1:
self.res = min(self.res, cur_sum) # 当前搜索到最后一行了,更新全局最小路径
return
# 否则的话,进入下一行
dfs(level+1, col, cur_sum)
dfs(level+1, col+1, cur_sum)
dfs(0, 0, 0)
return self.res
dfs + 记忆化
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
import functools
n = len(triangle)
@functools.lru_cache(None) # 缓存递归结果
def helper(level, i, j):
if level == n:
return 0
res = 0
a = float("inf")
b = float("inf")
if 0 <= i <len(triangle[level]):
a = helper(level+1, i, i+1) + triangle[level][i] # 如果(level, i)不越界,可选
if 0 <= j <len(triangle[level]):
b = helper(level+1, j, j+1) + triangle[level][j] # 如果(level, j)不越界,可选
res += min(a, b) # 自底向上到 (level, i) (level, j)的最小路径
return res
return helper(0, -1, 0)
动态规划,自底向上考虑,到节点[i][j]的最短路径之和为dp[i][j],状态转移方程为 dp[i][j] = min( dp[i-1][j], dp[i-1][j-1] ) + triangle[i][j]
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
if not triangle:
return 0
n = len(triangle)
dp = [[0]*(i+1) for i in range(n)]
dp[0][0] = triangle[0][0]
for i in range(1, n):
for j in range(i+1):
# 如果当前节点是第一列,或最后一列,那上层路径只可能来自于一个节点
if j == 0:
dp[i][j] = dp[i-1][j] + triangle[i][j]
elif j == i:
dp[i][j] = dp[i-1][j-1] + triangle[i][j]
else:
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]
return min(dp[-1])
倒着循环的话用一维数组就可以了,不停地覆盖,而且状态不会被污染,状态上一层状态更新都是来源于下一层的状态。
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
if not triangle:
return 0
n = len(triangle)
dp = triangle[-1]
for i in range(n-2, -1, -1):
for j in range(i+1):
dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j]
return dp[0]
152. 乘积最大子序列 https://leetcode-cn.com/problems/maximum-product-subarray/
给定一个整数数组 nums ,找出一个序列中乘积最大的连续子序列(该序列至少包含一个数)。
解:
如果不要求连续,直接把所有大于0的数拿出来就行了。
暴力,直接递归,搜索所有可能的子序列。超时。
class Solution:
def maxProduct(self, nums: List[int]) -> int:
if nums is None or len(nums) == 0:
return 0
res = float('-inf')
n = len(nums)
def dfs(start):
nonlocal res
if start == n:
return
for end in range(start, n):
cur = 1
for i in range(start, end+1):
cur *= nums[i]
if cur > res:
res = cur
dfs(start+1)
dfs(0)
return res
动态规划,同时维护一组最小的状态。a[i]为正,选择最大的dp[i-1],a[i]为负,选择最小的m[i-1]。
class Solution:
def maxProduct(self, nums: List[int]) -> int:
if nums is None or len(nums) == 0:
return 0
n = len(nums)
dp = [nums[0]]*n
m = [nums[0]]*n
for i in range(1, n):
dp[i] = max(dp[i-1]*nums[i], nums[i], m[i-1]*nums[i])
m[i] = min(dp[i-1]*nums[i], nums[i], m[i-1]*nums[i])
return max(dp)
# 节省空间
class Solution:
def maxProduct(self, nums: List[int]) -> int:
if nums is None or len(nums) == 0:
return 0
n = len(nums)
dp = nums[0]
m = nums[0]
res = nums[0]
for i in range(1, n):
# max 和 min 同时更新
dp, m = max(dp*nums[i], nums[i], m*nums[i]), min(dp*nums[i], nums[i], m*nums[i])
res = max(res, dp)
return res
121. 买卖股票的最佳时机 https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
解:
只能买卖一次,肯定在最低点买进,最高点卖出,但这个关系必须要服从时序。从前向后维护一个价格最低点,如果当天价格减去最低点得到的利润比目前的最大利润大,更新即可。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if prices is None or len(prices) <= 1:
return 0
lowest = prices[0]
res = 0
for i in range(1, len(prices)):
lowest = min(lowest, prices[i])
res = max(res, prices[i]-lowest)
return res
dp解法,类似与最大连续子序列和的问题。第i天的最大利润,要么是从i-1天之前就持有到第i天,利润为第i-1天的最大利润加上新一天的利润;要么直接就是i-1天买入i天卖出(因为只能买卖一次)。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if prices is None or len(prices) <= 1:
return 0
dp = [0]*len(prices)
for i in range(1,len(prices)):
dp[i] = max(dp[i-1] + prices[i]- prices[i-1], prices[i] - prices[i-1])
return max(dp)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if prices is None or len(prices) <= 1:
return 0
n = len(prices)
dp = 0
res = 0
for i in range(1, n):
dp = max(dp + prices[i] - prices[i-1], prices[i] - prices[i-1])
res = max(res, dp)
return res
通用dp框架
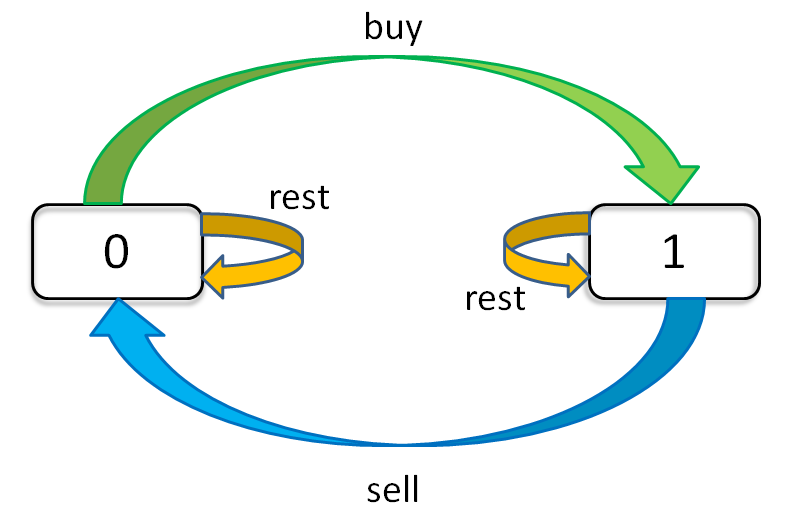
dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 为天数,K 为最多交易数、买进了就算开始交易,0表示不持股、1表示持股。dp[i][k][j]:第i天至多交易了k次{1, ..., K}、处于k状态{未持股、持股}的最大利润。
此问题共 n × K × 2 种状态。
for 0 <= i < n:
for 1 <= k <= K:
for s in {0, 1}:
dp[i][k][s] = max(buy, sell, rest)
初始状态:
dp[-1][k][0] = 0 # 还没开始,不持股,利润为0
dp[-1][k][1] = float('-inf') # 还没开始,不可能持有股票
dp[i][0][0] = 0 # 至多交易了0次,不持股,利润为0
dp[i][0][1] = float('-inf') # 至多交易了0次,不可能持股
状态转移:
# 第i天至多交易了k次、不持股 from {第i-1天至多交易了k次、不持股、第i天不操作, 第i-1天至多交易了k次、持股、第i天卖出}:{rest, sell}
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
# 第i天至多交易了k次、持股 from {第i-1天至多交易了k次、持股、第i天不操作, 第i-1天至多交易了k-1次、不持股、第i天买进}:{rest, buy}
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
#121,至多一次交易
dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i]) = max(dp[i-1][1][1], 0 - prices[i])
可以发现全是k=1的状态,不需要三维dp
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], - prices[i])
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
dp = [[0]*2 for _ in range(n)] # dp[i][j],第i天状态j{不持股、持股}最大利润,K=1每天都是至多交易了1次
for i in range(n):
# 处理初始状态
if i-1 == -1:
dp[i][0] = 0 # max(dp[-1][0], dp[-1][1]+prices[i])=max(0, -inf+prices[i])=0
dp[i][1] = -prices[i] # max(dp[-1][1], dp[-1][0]-prices[i])=max(-inf, 0-prices[i])=-prices[i]
else:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], - prices[i])
return dp[n-1][0]
# 可以发现i时刻状态转移只和相邻状态有关,直接滚动更新,降空间复杂度
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
# 初始状态
# dp[-1][1][0]=0, dp[-1][1][1]='-inf'
dp_i_0, dp_i_1 = 0, float('-inf')
for i in range(n):
dp_i_0 = max(dp_i_0, dp_i_1 + prices[i])
dp_i_1 = max(dp_i_1, - prices[i])
return dp_i_0
122. 买卖股票的最佳时机ii https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii/
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解:
贪心在之前已经讨论过了。这里只看用dp实现。第i天的最大利润,要么是第i-1天的最大利润(i天跌了,不操作),要么要么是第i-1天的最大利润加上新一天的利润(i天涨了,i-1天买入i天卖掉)。
状态转移方程为:dp[i] = dp[i-1] if prices[i] <= prices[i-1] else dp[i-1] + prices[i] -prices[i-1],遍历一次即可,O(n)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
dp = [0]*n
for i in range(1, n):
dp[i] = max(dp[i-1], dp[i-1] + prices[i] - prices[i-1])
return max(dp)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
res = 0
for i in range(1, n):
res = max(res, res + prices[i] - prices[i-1])
return res
通用dp,K=inf。如果k为正无穷,那么可以认为k=k-1。状态转移框架为
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]) = max(dp[i-1][k][1], dp[i-1][k][0] - prices[i])
不需要k了
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
dp = [[0]*2 for _ in range(n)] # dp[i][j],第i天状态j{不持股、持股}最大利润
for i in range(n):
# 处理初始状态
if i-1 == -1:
dp[i][0] = 0 # max(dp[-1][0], dp[-1][1]+prices[i])=max(0, -inf+prices[i])=0
dp[i][1] = -prices[i] # max(dp[-1][1], dp[-1][0]-prices[i])=max(-inf, 0-prices[i])=-prices[i]
else:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
return dp[n-1][0]
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
dp_i_0, dp_i_1 = 0, float('-inf')
for i in range(n):
tmp = dp_i_0 # 不要污染上一时刻的数据
dp_i_0 = max(dp_i_0, dp_i_1 + prices[i])
dp_i_1 = max(dp_i_1, tmp - prices[i]) # python同时赋就行,这里为了便于理解
return dp_i_0
309. 最佳买卖股票时机含冷冻期 https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
解:
K=inf,且每次卖出后要隔一天才能卖出。状态转移方程为:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-2][k-1][0] - prices[i]) = max(dp[i-1][k][1], dp[i-2][k][0] - prices[i])
把k拿掉
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
dp = [[0]*2 for _ in range(n)]
for i in range(n):
# 处理初始状态
if i == 0:
dp[i][0] = 0
dp[i][1] = -prices[i]
elif i == 1:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], - prices[i])
else:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])
return dp[n-1][0]
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
dp_i_0, dp_i_1 = 0, float('-inf')
dp_pre_0 = 0 # dp[i-2][0]
for i in range(n):
tmp = dp_i_0
dp_i_0 = max(dp_i_0, dp_i_1 + prices[i])
dp_i_1 = max(dp_i_1, dp_pre_0 - prices[i])
dp_pre_0 = tmp # 当前时刻的dp[i-1][0]是下一时刻的dp[i-2][0]
return dp_i_0
714.买卖股票的最佳时机含手续费 https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/
给定一个整数数组 prices,其中第 i 个元素代表了第 i 天的股票价格 ;非负整数 fee 代表了交易股票的手续费用。
你可以无限次地完成交易,但是你每次交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
解:
k=inf,只要从利润中把手续费减去即可。
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i] - fee)
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
if not prices:
return 0
n = len(prices)
dp = [[0]*2 for _ in range(n)] # dp[i][j],第i天状态j{不持股、持股}最大利润
for i in range(n):
# 处理初始状态
if i-1 == -1:
dp[i][0] = 0 # max(dp[-1][0], dp[-1][1]+prices[i]-fee)=max(0, -inf+prices[i]-fee)=0
dp[i][1] = -prices[i] # max(dp[-1][1], dp[-1][0]-prices[i])=max(-inf, 0-prices[i])=-prices[i]
else:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i] - fee)
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
return dp[n-1][0]
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
if not prices:
return 0
n = len(prices)
dp_i_0, dp_i_1 = 0, float('-inf')
for i in range(n):
tmp = dp_i_0
dp_i_0 = max(dp_i_0, dp_i_1 + prices[i] - fee)
dp_i_1 = max(dp_i_1, tmp - prices[i])
return dp_i_0
123. 买卖股票的最佳时机iii https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iii/
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解:
K=2,这题k是不能直接消掉的,状态转移时要对k进行穷举。
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
max_k = 2
dp = [[[0]*2 for _ in range(max_k+1)] for _ in range(n)]
for i in range(n):
for k in range(max_k, 0, -1):
if i == 0:
dp[i][k][0] = 0
dp[i][k][1] = -prices[i]
else:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
return dp[n-1][max_k][0]
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
max_k = 2
dp_i_1_0, dp_i_1_1 = 0, float('-inf')
dp_i_2_0, dp_i_2_1 = 0, float('-inf')
for i in range(n):
dp_i_2_0 = max(dp_i_2_0, dp_i_2_1 + prices[i])
dp_i_2_1 = max(dp_i_2_1, dp_i_1_0 - prices[i])
dp_i_1_0 = max(dp_i_1_0, dp_i_1_1 + prices[i])
dp_i_1_1 = max(dp_i_1_1, - prices[i])
return dp_i_2_0
188. 买卖股票的最佳时机iv https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv/
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
解:
股票买卖系列的基本点,把这题dp搞懂的话这个系列问题不大。状态定义+转移方程,三维的dp,最完整的情况。直接做超时的话,考虑一下如果K > n/2就退化成任意交易次数,直接贪心。
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
max_k = k
if 2 * max_k > n: # 如果k超过n的一半,问题就退化成了任意交易次数的情况,因为任何一笔交易都不能重叠
return self.greedy(prices)
dp = [[[0]*2 for _ in range(max_k+1)] for _ in range(n)]
for i in range(n):
for k in range(max_k, 0, -1):
if i == 0:
dp[i][k][0] = 0
dp[i][k][1] = -prices[i]
else:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
return dp[n-1][max_k][0]
def greedy(self, prices):
"""贪心,只要第二天涨了,就前一天买入第二天卖出"""
p = 0
for i in range(1, len(prices)):
cur = prices[i] - prices[i-1]
if cur > 0:
p += cur
return p if p else 0
300. 最长上升子序列 https://leetcode-cn.com/problems/longest-increasing-subsequence/
给定一个无序的整数数组,找到其中最长上升子序列的长度。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?
解:
子序列不必连续,但前后位置不能变。
暴力dfs,O(2n),超时
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if not nums:
return 0
n = len(nums)
def helper(prev, curpos):
"""prev当前最大子序列的最后一个元素, curpos当前位置"""
if curpos == n:
return 0
taken = 0
if nums[curpos] > prev: # 如果上升且加到子序列中的情况
taken = 1 + helper(nums[curpos], curpos+1)
nottaken = helper(prev, curpos+1) # 不选当前位置元素,可能是不上升,也可能是上升但不选的回溯
return max(taken, nottaken)
return helper(float('-inf'), 0)
dfs + 记忆化。memo[i][j] 表示使用 nums[i] 作为上一个被认为包含/不包含在子序列中时子序列可能的长度,其中 nums[j] 作为当前被认为包含/不包含在子序列中的元素。还是超时。
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if not nums:
return 0
n = len(nums)
memo = [[-1]*n for _ in range(n+1)] # memo[i][j] 子序列长度
def helper(prevpos, curpos, memo):
"""prev当前最大子序列的最后一个元素索引, curpos当前元素索引"""
if curpos == n:
return 0
if memo[prevpos+1][curpos] >= 0: # 多一行prevpos用于处理curpos=0的情况。
return memo[prevpos+1][curpos]
taken = 0
if prevpos < 0 or nums[curpos] > nums[prevpos]: # 如果上升且加到子序列中的情况
taken = 1 + helper(curpos, curpos+1, memo)
nottaken = helper(prevpos, curpos+1, memo) # 不选当前位置元素,可能是不上升,也可能是上升但不选的回溯
memo[prevpos+1][curpos] = max(taken, nottaken)
return memo[prevpos+1][curpos]
return helper(-1, 0, memo)
动态规划,这题是最优子结构,当选到某个位置元素进入子序列时,不管其后面的元素,其前面的最长子序列就已经确定了。
dp[i]表示从头开始到第i元素且把i元素选上的情况下,最长上升子序列长度。最后要的结果为max(dp)。dp[i] = max(dp[0], ..., dp[j], ..., dp[i-1]) +1 且a[i] 要大于a[j]。因为从上一个被选上的元素到当前被选上的i中间可能是有跳过的。O(n2)
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if not nums:
return 0
n = len(nums)
dp = [0] * n
for i in range(n):
max_prev = 0
for j in range(i):
if nums[i] > nums[j]:
max_prev = max(max_prev, dp[j])
dp[i] = max_prev + 1
return max(dp)
动态规划 + 二分搜索,把上面方法中内层 j 循环替换成二分。始终维护一个数组LIS为要求的上升子序列,对每一个a[i],插入到LIS中(二分法找到第一个比a[i]大的数替换掉,因为这样尽可能多的让后面符合条件的数进来,要缩一下上界。如果a[i]比LIS所有都大就直接append),最后LIS的长度即为所求。O(nlogn)
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if not nums:
return 0
n = len(nums)
LIS = []
for i in range(n):
if not LIS or nums[i] > LIS[-1]:
LIS.append(nums[i])
else:
index = self.binarySearch(LIS, nums[i])
LIS[index] = nums[i]
return len(LIS)
def binarySearch(self, array, target):
"""返回第一个比target大的元素索引"""
if not array:
return
low, high = 0, len(array) - 1
while low <= high:
mid = low + (high-low)//2
if array[mid] < target:
low = mid + 1
elif array[mid] > target:
high = mid - 1
else:
return mid
return low
354. 俄罗斯套娃信封问题 https://leetcode-cn.com/problems/russian-doll-envelopes/
给定一些标记了宽度和高度的信封,宽度和高度以整数对形式 (w, h) 出现。当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
说明:
不允许旋转信封。
示例:
输入: envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出: 3
解释: 最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。
解:
这道题是最长上升子序列的升维,要先对宽度进行升序排列,然后对宽度相同的按高度降序排序。最后对高度数组进行最长上升子序列的求解
class Solution: def maxEnvelopes(self, envelopes: List[List[int]]) -> int: if not envelopes: return 0 n = len(envelopes) nums = sorted(envelopes, key=lambda x: [x[0], -x[1]]) dp = [1] * n for i in range(n): for j in range(i-1, -1, -1): if nums[i][1] > nums[j][1]: dp[i] = max(dp[i], dp[j] + 1) return max(dp)
用二分法来优化
class Solution:
def maxEnvelopes(self, envelopes: List[List[int]]) -> int:
if not envelopes:
return 0
n = len(envelopes)
nums = sorted(envelopes, key=lambda x: [x[0], -x[1]])
LIS = []
for i in range(n):
if not LIS or nums[i][1] > LIS[-1]:
LIS.append(nums[i][1])
else:
index = self.binarySearch(LIS, nums[i][1])
LIS[index] = nums[i][1]
return len(LIS)
def binarySearch(self, array, target):
"""返回第一个比target大的元素索引"""
if not array:
return
low, high = 0, len(array) - 1
while low <= high:
mid = low + (high-low)//2
if array[mid] < target:
low = mid + 1
elif array[mid] > target:
high = mid - 1
else:
return mid
return low
322. 零钱兑换 https://leetcode-cn.com/problems/coin-change/
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
解:
仔细想清楚的话,这题其实和斐波那契数列是一样的,只不过台阶数变成了总金额。
暴力dfs,对每一种可能的组合都走一边,取硬币数最小的组合。指数级复杂度O(knk)。
import sys
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
if amount == 0:
return -1
ans = sys.maxsize
for coin in coins:
if amount < coin: # 金额不可达
continue
subProblem = self.coinChange(coins, amount-coin)
if subProblem == -1: # 子问题无解
continue
ans = min(ans, subProblem + 1)
return -1 if ans == sys.maxsize else ans
dfs+记忆化,先选大面额的硬币,O(kn)
import sys
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
if not coins:
return -1
coins.sort(reverse=True)
memo = [-2] * (amount+1) # memo[amount]表示凑到金额为amount的最少硬币数
def helper(coins, amount, memo):
if amount == 0:
return 0
if memo[amount] != -2:
return memo[amount]
ans = sys.maxsize
for coin in coins:
if amount < coin: # 金额不可达
continue
subProblem = helper(coins, amount-coin, memo)
if subProblem == -1: # 子问题无解
continue
ans = min(ans, subProblem + 1)
memo[amount] = -1 if ans == sys.maxsize else ans # 记录本轮答案
return memo[amount]
return helper(coins, amount, memo)
动态规划,f(amount) = 1 + min{ f(amount - ci) | i in [1, k] },O(kn)
import sys
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
if not coins:
return 0
dp = [sys.maxsize] * (amount+1)
dp[0] = 0
for i in range(1, amount+1):
for j in range(len(coins)):
if i < coins[j]:
continue
dp[i] = min(dp[i], dp[i - coins[j]] + 1)
return -1 if dp[amount] == sys.maxsize else dp[amount]
72. 编辑距离 https://leetcode-cn.com/problems/edit-distance/
给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
解:
状态定义。dp[i],一维状态是不够的。dp[i][j] 表示单词1的前i个字符,要替换到单词2的前j个字符,最少需要多少步数。dp[m][n]即为最后要求的解。
状态转移。
如果w1[i]、w2[j]字符相同,不用做任何操作,dp[i][j] = dp[i-1][j-1]。
否则,可以有三种操作,dp[i][j] = 1 + min( dp[i-1][j], dp[i][j-1], dp[i-1][j-1] ) 依次为w1插入,w2插入,w1w2替换
O(mn)
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
m, n = len(word1), len(word2)
dp = [[0]*(n+1) for _ in range(m+1)]
# 初始状态
for i in range(m+1):
dp[i][0] = i # w1前i个匹配到w2前0个,i次删除
for j in range(n+1):
dp[0][j] = j # w2前j个匹配到w1前0个,j次删除
for i in range(1, m+1):
for j in range(1, n+1):
if word1[i-1] == word2[j-1]: # w1第i个字符和w2第j个字符如果相同
dp[i][j] = dp[i-1][j-1] # 不用操作
else:
dp[i][j] = 1 + min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) # 三种操作,w1删除/插入还是w2插入/删除不用细抠
return dp[m][n]
5. 最长回文子串 https://leetcode-cn.com/problems/longest-palindromic-substring/
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
解:
暴力法,选出左右子串可能开始和结束的位置,并检验其是否是回文。直接嵌套两层循环即可,这里强行写成dfs再继续练习。O(n3)
class Solution:
def longestPalindrome(self, s: str) -> str:
if not s:
return ''
res = ''
n = len(s)
def isValid(s):
str_len = len(s)
for i in range(str_len//2):
if s[i] != s[str_len-1-i]:
return False
return True
def helper(start):
nonlocal res
if start == n:
return
for end in range(start, n):
if isValid(s[start: end+1]):
res = s[start: end+1] if end-start+1 > len(res) else res
helper(start+1)
helper(0)
return res
class Solution:
def longestPalindrome(self, s: str) -> str:
if not s:
return ''
res = ''
n = len(s)
def isValid(s):
str_len = len(s)
for i in range(str_len//2):
if s[i] != s[str_len-1-i]:
return False
return True
for i in range(n):
for j in range(i, n):
if isValid(s[i:j+1]):
res = s[i:j+1] if j-i+1 > len(res) else res
return res
如何优化暴力解法,动态规划。定义p(i, j) = True if s[i, j] 是 回文 else False,那么显然P(i, j) = p(i+1, j-1) and (s[i] == s[j])。只有一个字符和两个字符的情况单独考虑。要注意的是,递推时i的取值由i+1决定,所以i要倒着推。
class Solution:
def longestPalindrome(self, s: str) -> str:
if not s:
return ''
res = ''
n = len(s)
p = [[-1 for _ in range(n)] for _ in range(n)]
for i in range(n-1, -1, -1):
for j in range(i, n):
p[i][j] = (j==i or j-i==1 or p[i+1][j-1]) and (s[i] == s[j])
if p[i][j] and j-i+1 > len(res):
res = s[i:j+1]
return res
由于i是倒着推的,所以求第i行时只需要i+1行的信息,而这一行的p[j]的取值需要知道下一行的p[j-1]的信息,所以倒着推j的话可以把空间降到一维。
class Solution:
def longestPalindrome(self, s: str) -> str:
if not s:
return ''
res = ''
n = len(s)
p = [-1 for _ in range(n)]
for i in range(n-1, -1, -1):
for j in range(n-1, i-1, -1):
p[j] = (j==i or j-i==1 or p[j-1]) and (s[i] == s[j])
if p[j] and j-i+1 > len(res):
res = s[i:j+1]
return res
中心扩散。每次循环选择一个中心(一个字符或两个字符之间),进行左右扩展,判断左右字符是否相等即可。
class Solution:
def longestPalindrome(self, s: str) -> str:
if not s:
return ''
def expand(s, left, right):
"""从中心向外扩展到最长的回文s[left]...s[right]"""
while left >= 0 and right < len(s) and s[left]==s[right]:
left -= 1
right += 1
return left+1, right-1 # 返回中心扩散得到的最长回文字符的起止点
n = len(s)
res = ''
for i in range(n):
l1, r1 = expand(s, i, i)
l2, r2 = expand(s, i, i+1)
if r1-l1+1 > len(res):
res = s[l1: r1+1]
if r2-l2+1 > len(res):
res = s[l2: r2+1]
return res
Manacher's Algorithm 马拉车算法,可以降到O(n)。
10. 正则表达式匹配 https://leetcode-cn.com/problems/regular-expression-matching/
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
说明:
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
解:
先看第一个元素能不能匹配,如果可以匹配就递归地看后面能不能匹配。如果p[0]取值为s[0]或者'.',第一个元素都是可以匹配的。
然后p[1]如果是'*',那么可以让前一个字符重复任意次数,到底重复多少次交给递归解决,当前的选择就两个:匹配0次,匹配1次,两种操作有一种使得剩下的字符串能够匹配,那么初始时匹配串和模式串就可以被匹配。
如果有字符和'*'结合,那么或者匹配该字符0次、p跳过该字符和'*',继续匹配s;或者在p[0]和s[0]匹配的前提下,删除匹配串的第一个字符,再用p去匹配。如果没有'*',那么就必须得p[0]和s[0]匹配上,然后再拿p[1:]去匹配s[1:]。
暴力递归,超时。
class Solution:
def isMatch(self, s: str, p: str) -> bool:
if not p:
return not s
# p[0]能否匹配上s[0],就两种情况p[0]==s[0],或者p[0]可以任意
first_match = bool(s) and p[0] in {s[0], '.'}
if len(p) >= 2 and p[1] == '*':
return self.isMatch(s, p[2:]) or (first_match and self.isMatch(s[1:], p))
else: # 如果p[1]不是'*'那就看p[0]有没有直接匹配上,以及s[1:]和p[1:]是否匹配
return first_match and self.isMatch(s[1:], p[1:])
dfs+记忆化,用memo[(i, j)]来表示s[i:] 和p[j:]是否匹配。
class Solution:
def isMatch(self, s: str, p: str) -> bool:
memo = dict()
def helper(i, j):
if (i, j) in memo:
return memo[(i, j)]
if j == len(p): # p串到最后了
return i == len(s)
first_match = i < len(s) and p[j] in {s[i], '.'}
if j <= len(p)-2 and p[j+1] == '*':
ans = helper(i, j+2) or (first_match and helper(i+1, j))
else:
ans = first_match and helper(i+1, j+1)
memo[(i, j)] = ans
return ans
return helper(0, 0)
动态规划,自底向上,dp[i][j] 表示s[i:] 和 p[j:]是否匹配。
class Solution:
def isMatch(self, s: str, p: str) -> bool:
dp = [[False] * (len(p)+1) for _ in range(len(s)+1)]
dp[-1][-1] = True # []匹配[]
for i in range(len(s), -1, -1):
for j in range(len(p)-1, -1, -1):
first_match = i < len(s) and p[j] in {s[i], '.'}
if j <= len(p)-2 and p[j+1] == '*':
dp[i][j] = dp[i][j+2] or (first_match and dp[i+1][j])
else:
dp[i][j] = first_match and dp[i+1][j+1]
return dp[0][0]
32. 最长有效括号 https://leetcode-cn.com/problems/longest-valid-parentheses/
给定一个只包含 '(' 和 ')' 的字符串,找出最长的包含有效括号的子串的长度。
示例 1:
输入: "(()"
输出: 2
解释: 最长有效括号子串为 "()"
示例 2:
输入: ")()())"
输出: 4
解释: 最长有效括号子串为 "()()"
解:
暴力,两层迭代遍历所有可能的起止点,对每个子串判断一下是否有效,维护一个全局最长距离
class Solution:
def longestValidParentheses(self, s: str) -> int:
def isValid(s):
if not s:
return False
stack = []
for i in range(len(s)):
if s[i] == ')':
if not stack or stack[-1] != '(':
return False
stack.pop()
else:
stack.append(s[i])
if stack:
return False
return True
res = 0
for i in range(len(s)):
for j in range(i+1, len(s), 2):
if isValid(s[i:j+1]):
res = max(res, j-i+1)
return res
动态规划,定义dp[i] 表示以第i个元素结尾的最长有效字符串的长度。显然有效字符串必须以')'结尾,那么以'('结尾的子字符串对应的dp数组值一定为0。
如果s[i] = ')' 且s[i-1]='(',那么dp[i] = dp[i-2] + 2,这个原因比较明显,s[i-1]和s[i]正好凑了一对有效括号长度为2
如果s[i] = ')' 且s[i-1] = ')',dp[i] = dp[i-1] + dp[i-dp[i-1] - 2] + 2,如果倒数第二个')'是一个有效子串sb的一部分,那么就越过这个子串再往前看当前的这个')'能不能成为有效子串的结尾。如果sb前面正好是'(',越过sb之后就根第一种情况一致了,dp[i-dp[i-1]-2] + 2,再加上sb的长度即可。
class Solution:
def longestValidParentheses(self, s: str) -> int:
if not s:
return 0
n = len(s)
dp = [0] * n
res = 0
for i in range(1, n):
if s[i] == ')':
if s[i-1] == '(':
dp[i] = dp[i-2] + 2 if i >= 2 else 2
elif i-dp[i-1] > 0 and s[i-dp[i-1]-1] == '(':
dp[i] = dp[i-1] + dp[i-dp[i-1]-2] + 2 if i-dp[i-1]>=2 else dp[i-1] + 2
res = max(res, dp[i])
return res
对于这种括号匹配问题,一般都是使用栈。先找到所有可以匹配的索引号,然后找出最长连续数列!
例如:s = )(()()),我们用栈可以找到,位置 2 和位置 3 匹配,位置 4 和位置 5 匹配,位置 1 和位置 6 匹配,这个数组为:2,3,4,5,1,6 这是通过栈找到的,按递增排序得到 1,2,3,4,5,6。找出该数组的最长连续数列的长度就是最长有效括号长度,所以时间复杂度来自排序:O(nlogn)。接下来思考,是否可以省略排序的过程,在弹栈时候进行操作呢?
用栈在遍历给定字符串的过程中去判断到目前为止扫描的子字符串的有效性,同时能得到最长有效字符串的长度。我们首先将 -1 放入栈顶。
对于遇到的每个‘(’ ,我们将它的下标放入栈中。
对于遇到的每个 ‘)’ ,我们弹出栈顶的元素并将当前元素的下标与弹出元素下标作差,得出当前有效括号字符串的长度。通过这种方法,我们继续计算有效子字符串的长度,并最终返回最长有效子字符串的长度。时间复杂度为O(n)
class Solution:
def longestValidParentheses(self, s: str) -> int:
if not s:
return 0
n = len(s)
res = 0
stack = [-1]
for i in range(n):
if s[i] == '(': # 如果遍历到‘(’就把当前索引i压栈
stack.append(i)
else:
stack.pop() # 如果遍历到‘)’,弹出栈顶
if not stack: # 如果栈空,说明前面已经配好对了,当前i是那个多余的‘)’,索引i压栈
stack.append(i)
else:
res = max(res, i - stack[-1]) # 栈不空的话i-peek即为有效子串长度
return res



